- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
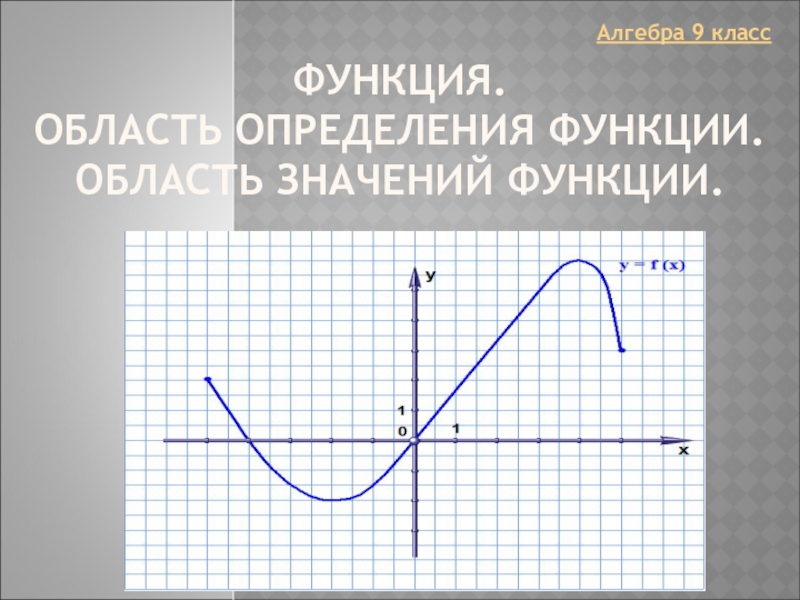
Презентация, доклад к уроку Область определения и область значения функции 9 класс, алгебра
Содержание
- 1. Презентация к уроку Область определения и область значения функции 9 класс, алгебра
- 2. ДАВАЙТЕ ВСПОМНИМ:Какую зависимость называют функцией? Как читают
- 3. Определение функции. Обозначение функции.
- 4. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ. Область определения функции
- 5. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ. Область значений функции
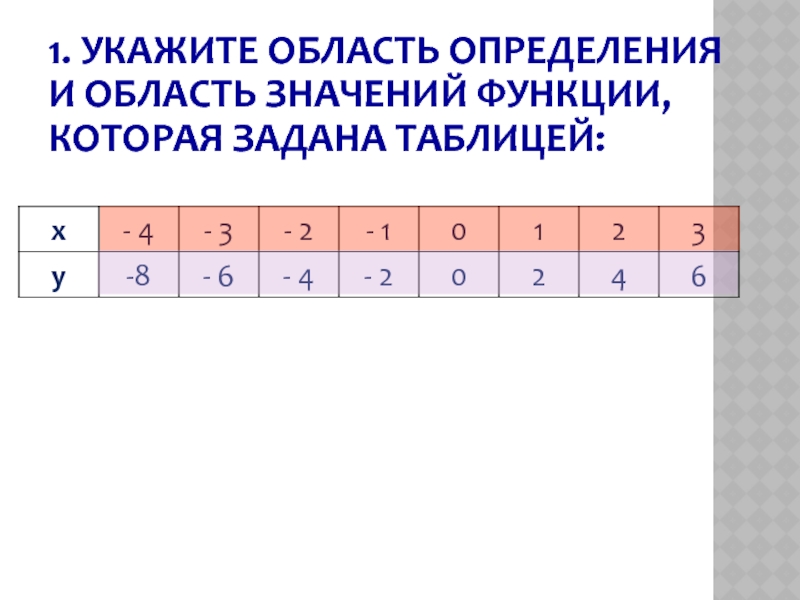
- 6. 1. УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ, КОТОРАЯ ЗАДАНА ТАБЛИЦЕЙ:
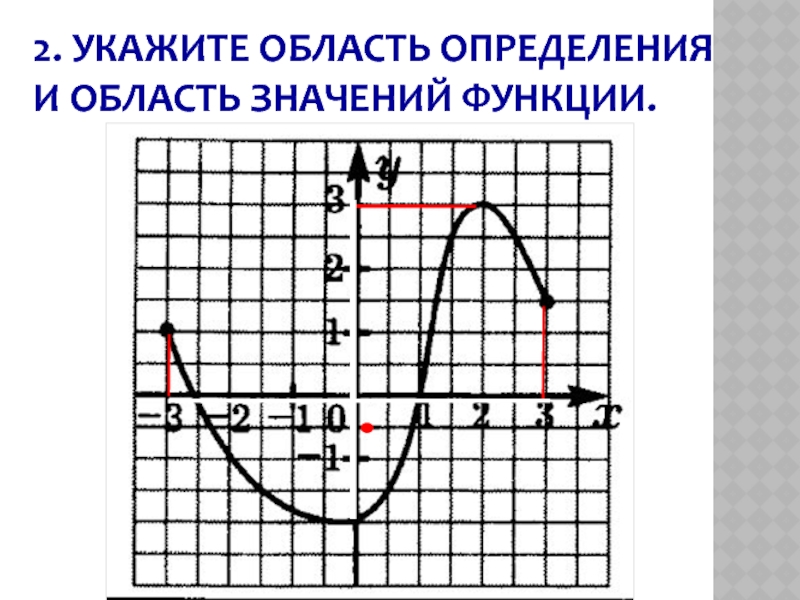
- 7. 2. УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ.
- 8. 3. ФУНКЦИЯ ЗАДАНА ГРАФОМ. ЗАПОЛНИТЕ ПРОПУСКИ.g(2) =
- 9. f(-3) = f(- 1) = f(x) =
- 10. 5. ФУНКЦИЯ ЗАДАНА ФОРМУЛОЙ. НАЙДИТЕ:а) f(2) =?б) D(f) = ?Решение:а) f(16) =?б) D(f) = ?Решение:
- 11. ГРАФИК ФУНКЦИИ
- 12. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ЛИНЕЙНОЙ ФУНКЦИИ
- 13. ОБЛАСТЬ ЗНАЧЕНИЙ ЛИНЕЙНОЙ ФУНКЦИИ
- 14. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ЛИНЕЙНОЙ ФУНКЦИИ
- 15. ОБЛАСТЬ ЗНАЧЕНИЙ ЛИНЕЙНОЙ ФУНКЦИИ
- 16. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ
- 17. ОБЛАСТЬ ЗНАЧЕНИЙ ПРАМОЙ ПРОПОРЦИОНАЛЬНОСТИ Y(Х
- 18. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ ,
- 19. ОБЛАСТЬ ЗНАЧЕНИЙ ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ, Х≠0
- 20. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ,
- 21. ОБЛАСТЬ ЗНАЧЕНИЙ КВАДРАТИЧНОЙ ФУНКЦИИ,
- 22. ОБЛАСТЬ
- 23. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
- 24. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
- 25. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
- 26. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
- 27. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
- 28. НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ - D(У)-54D(у)= [-5; 4,5]
- 29. НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ - Е(У)-25Е(у)= [-2; 5]
- 30. ПО ГРАФИКУ ОПРЕДЕЛИТЕ ПРОМЕЖУТОК НА КОТОРОМ ОПРЕДЕЛЕНА ДАННАЯ ФУНКЦИЯ-63D(у)= [-6; 3,5]
- 31. ПО ГРАФИКУ ОПРЕДЕЛИТЕ ПРОМЕЖУТОК НА КОТОРОМ ОПРЕДЕЛЕНА ДАННАЯ ФУНКЦИЯ-24Е(у)= [-2; 4]
- 32. НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ-55D(у)= [-5; 5]
- 33. НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ-26Е(у)= [-2; 6]
- 34. -44[ -4;4)3( -1;3]а)б)в)г)д)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ
- 35. НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ5( -1;5]-34[ -3;4)а)б)в)г)д)
- 36. -24[ -2;4)4[ -1;4]а)б)в)г)д)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ
- 37. б)в)г)-42[ -4;2]2[ -1;2]д)а)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ
Слайд 2ДАВАЙТЕ ВСПОМНИМ:
Какую зависимость называют функцией?
Как читают запись y = f(x)?
Что называют
Слайд 4ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ.
Область определения функции у(х)
это все значения
Обозначение
области определения - D(у)
Слайд 5ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ.
Область значений функции у(х)
это все значения
Обозначение области значений - Е(у)
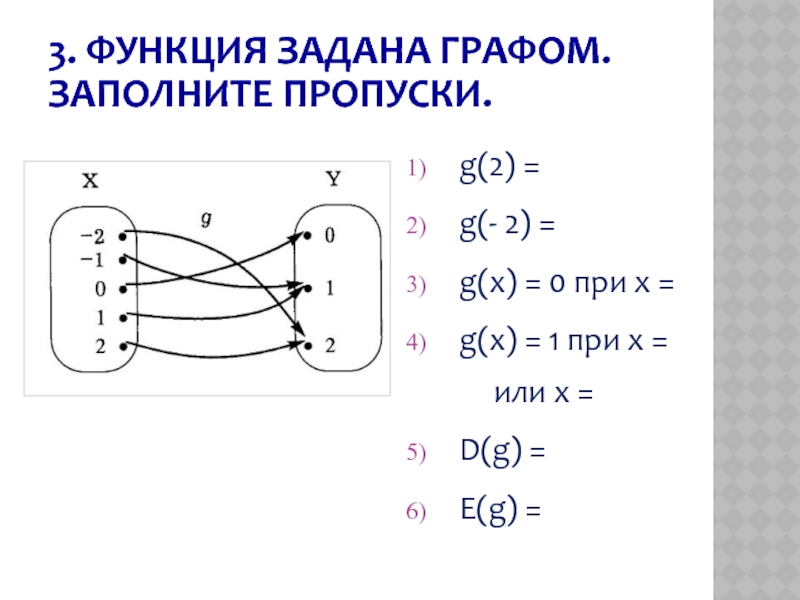
Слайд 83. ФУНКЦИЯ ЗАДАНА ГРАФОМ. ЗАПОЛНИТЕ ПРОПУСКИ.
g(2) =
g(- 2) =
g(x)
g(x) = 1 при х = или х =
D(g) =
E(g) =
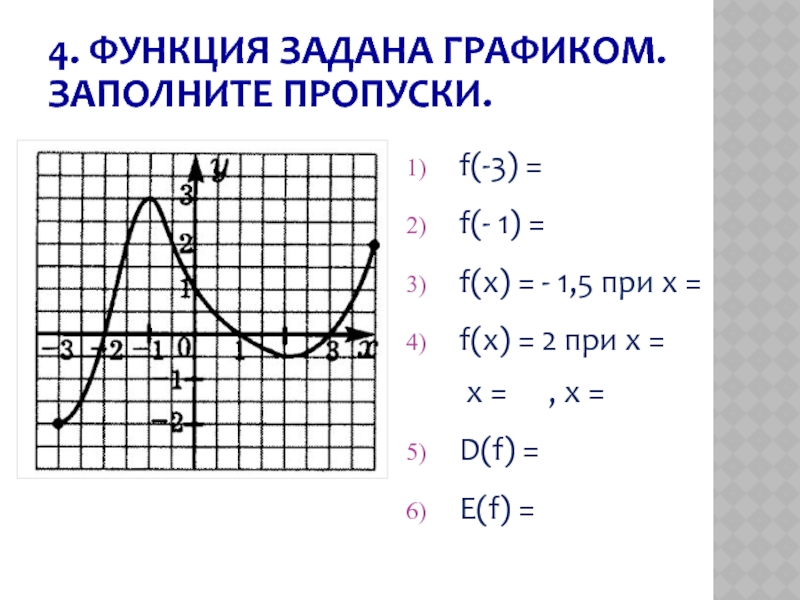
Слайд 9f(-3) =
f(- 1) =
f(x) = - 1,5 при x
f(x) = 2 при х = х = , x =
D(f) =
E(f) =
4. ФУНКЦИЯ ЗАДАНА ГРАФИКОМ. ЗАПОЛНИТЕ ПРОПУСКИ.
Слайд 105. ФУНКЦИЯ ЗАДАНА ФОРМУЛОЙ. НАЙДИТЕ:
а) f(2) =?
б) D(f) = ?
Решение:
а) f(16)
б) D(f) = ?
Решение:
Слайд 12
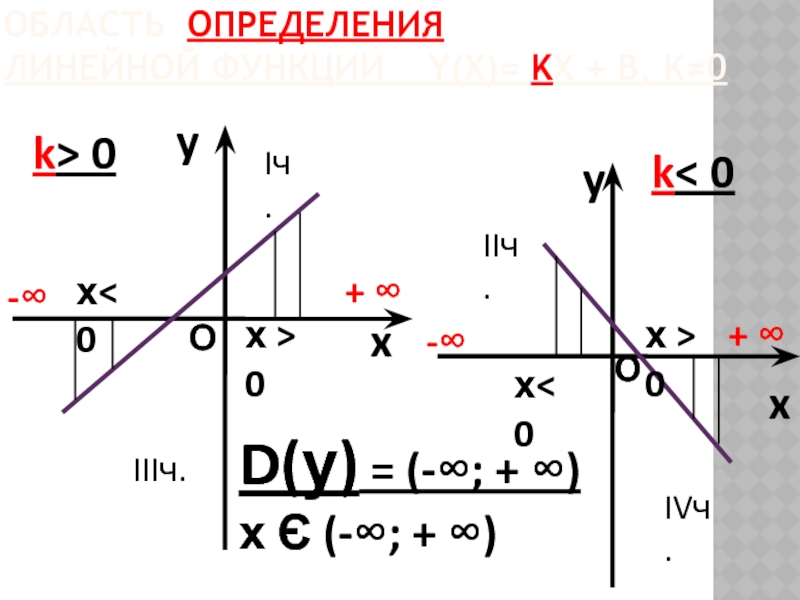
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ
ЛИНЕЙНОЙ ФУНКЦИИ Y(Х)= KX + B, K≠0
y
x
k>
y
x
k< 0
D(у) = (-∞; + ∞)
х Є (-∞; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
х< 0
х< 0
х > 0
х > 0
Iч.
IIIч.
IIч.
IVч.
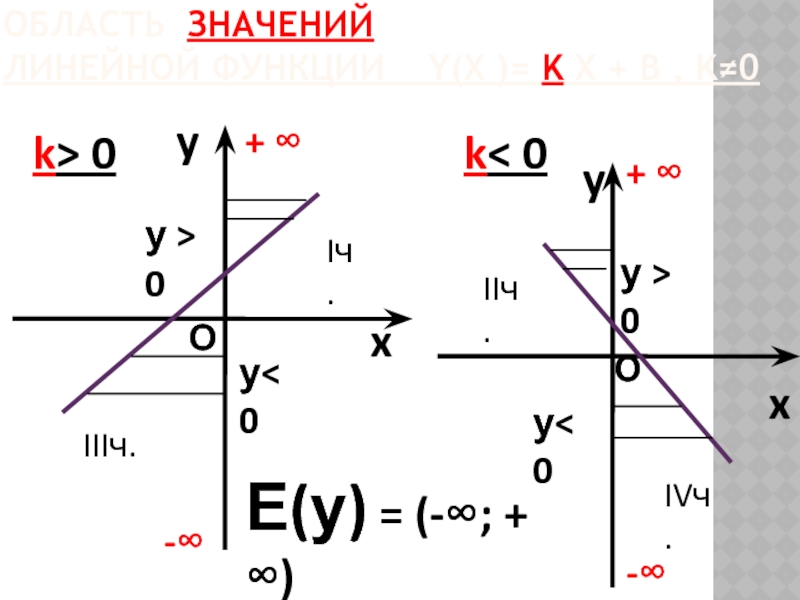
Слайд 13 ОБЛАСТЬ ЗНАЧЕНИЙ ЛИНЕЙНОЙ ФУНКЦИИ Y(Х )= K X +
y
x
k> 0
y
x
k< 0
Е(у) = (-∞; + ∞)
у(х) Є (-∞; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
у< 0
у< 0
у > 0
у > 0
Iч.
IIIч.
IIч.
IVч.
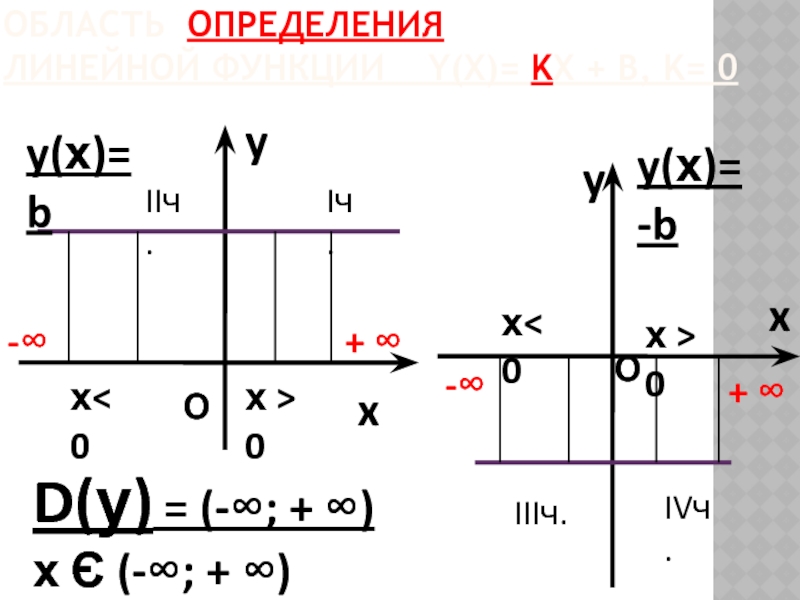
Слайд 14 ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ЛИНЕЙНОЙ ФУНКЦИИ Y(Х)= KX + B, K=
y
x
y(х)= b
y
x
y(х)= -b
D(у) = (-∞; + ∞)
х Є (-∞; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
х< 0
х< 0
х > 0
х > 0
Iч.
IIч.
IIIч.
IVч.
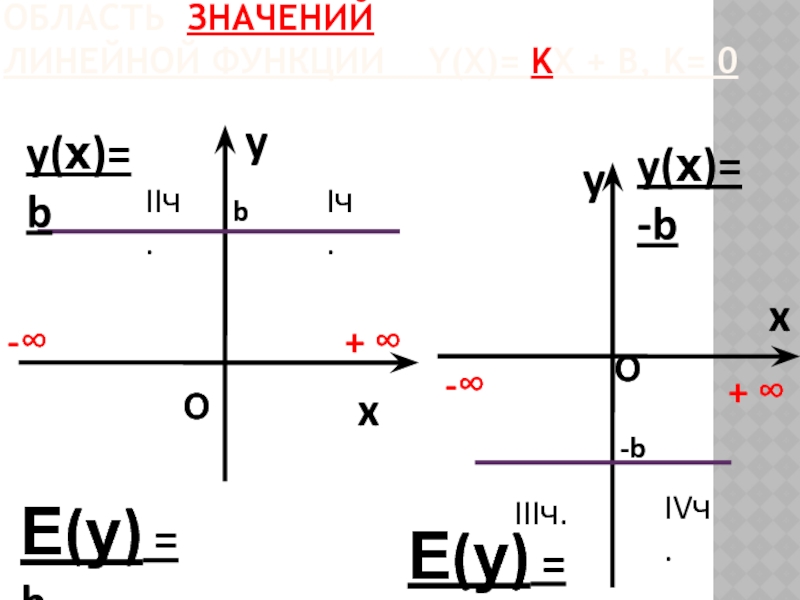
Слайд 15
ОБЛАСТЬ ЗНАЧЕНИЙ
ЛИНЕЙНОЙ ФУНКЦИИ Y(Х)= KX + B, K= 0
y
x
y(х)=
y
x
y(х)= -b
Е(у) = b
-∞
+ ∞
-∞
+ ∞
О
О
Iч.
IIч.
IIIч.
IVч.
Е(у) = -b
b
-b
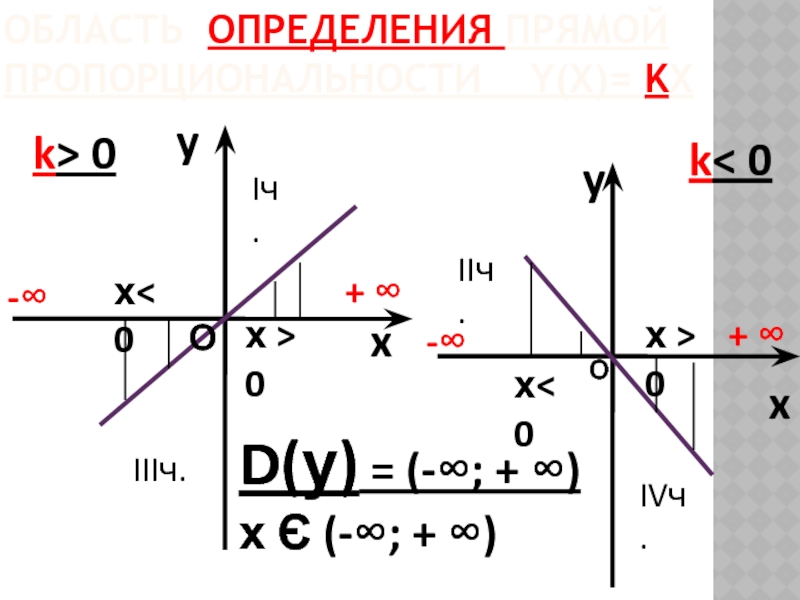
Слайд 16
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ПРЯМОЙ ПРОПОРЦИОНАЛЬНОСТИ Y(Х)= KX
y
x
k> 0
y
x
k< 0
D(у)
х Є (-∞; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
х< 0
х< 0
х > 0
х > 0
Iч.
IIIч.
IIч.
IVч.
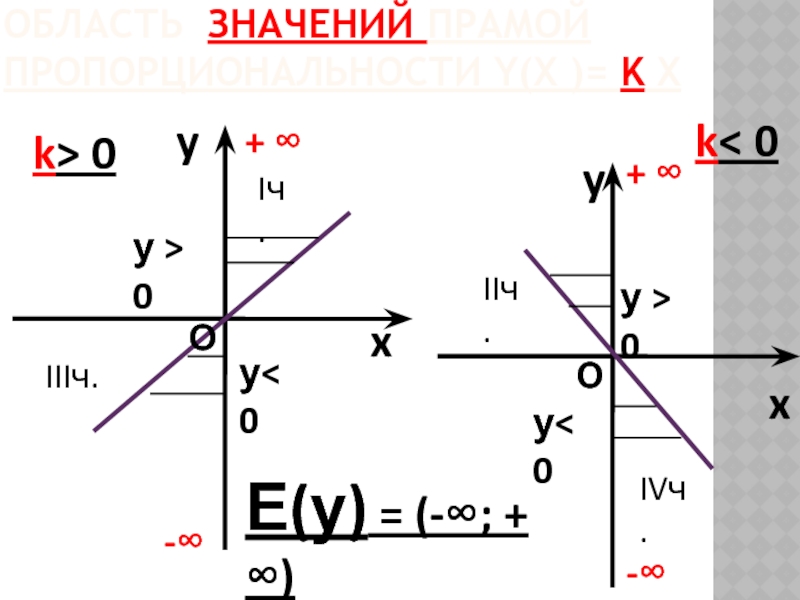
Слайд 17
ОБЛАСТЬ ЗНАЧЕНИЙ ПРАМОЙ ПРОПОРЦИОНАЛЬНОСТИ Y(Х )= K X
y
x
k> 0
y
x
k< 0
Е(у)
у(х) Є (-∞; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
у< 0
у< 0
у > 0
у > 0
Iч.
IIIч.
IIч.
IVч.
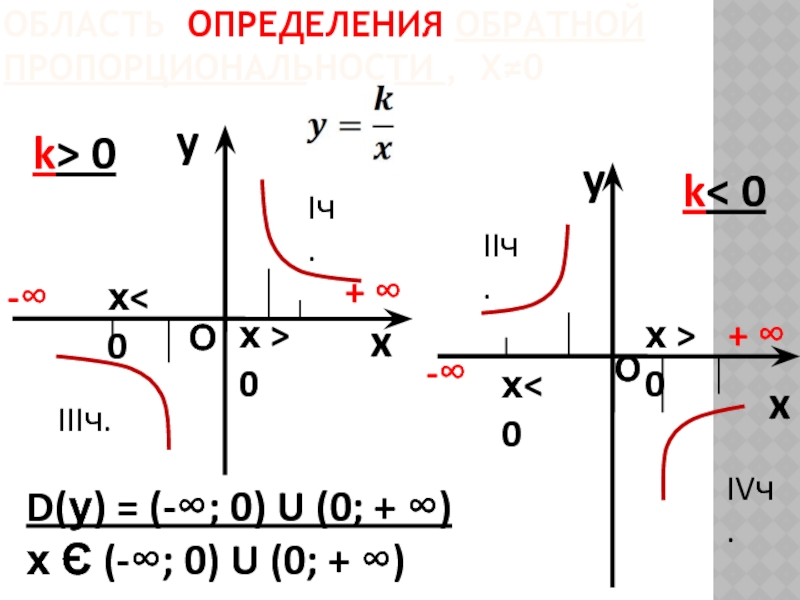
Слайд 18
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ , Х≠0
y
x
k> 0
y
x
k< 0
D(у) = (-∞;
х Є (-∞; 0) U (0; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
х< 0
х< 0
х > 0
х > 0
Iч.
IIIч.
IIч.
IVч.
Слайд 19
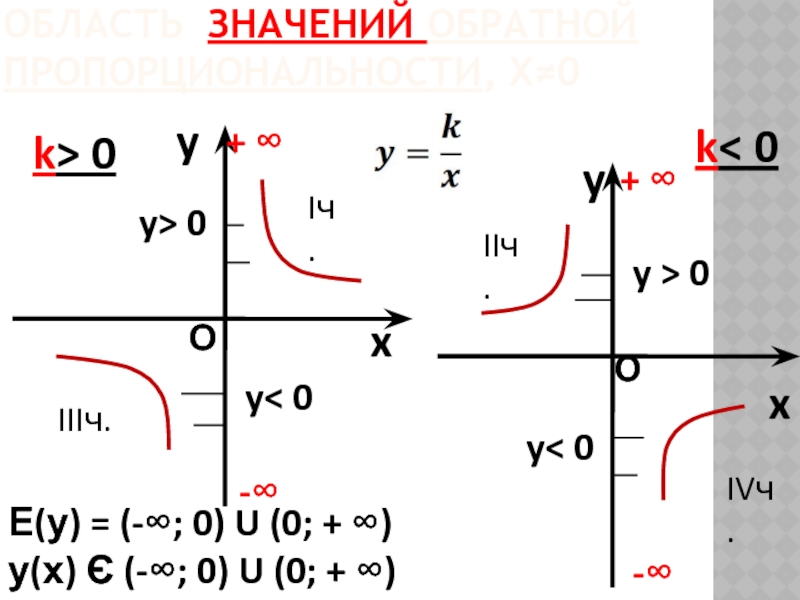
ОБЛАСТЬ ЗНАЧЕНИЙ ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ, Х≠0
y
x
k> 0
y
x
k< 0
Е(у) = (-∞; 0)
у(х) Є (-∞; 0) U (0; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
y< 0
y< 0
y> 0
y > 0
Iч.
IIIч.
IIч.
IVч.
Слайд 20
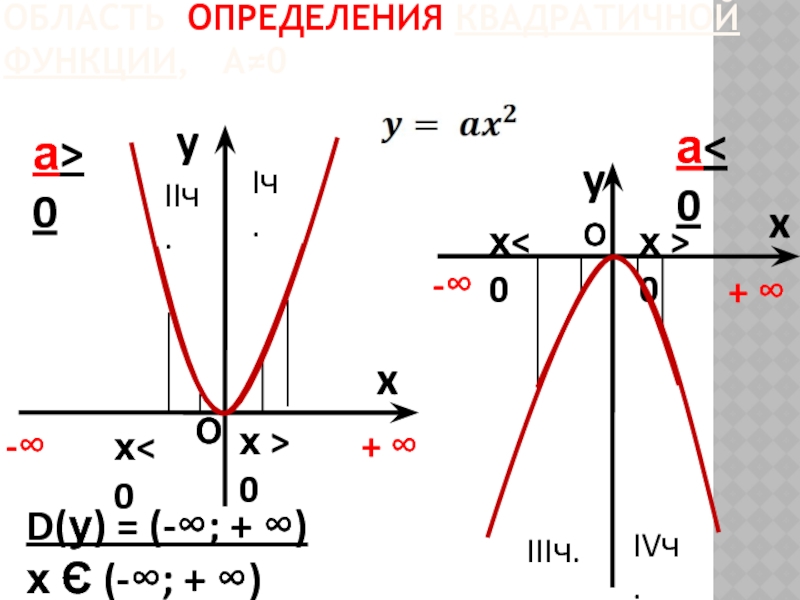
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ, А≠0
y
x
а> 0
y
x
а< 0
D(у) = (-∞;
х Є (-∞; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
х< 0
х< 0
х > 0
х > 0
Iч.
IIIч.
IIч.
IVч.
Слайд 21
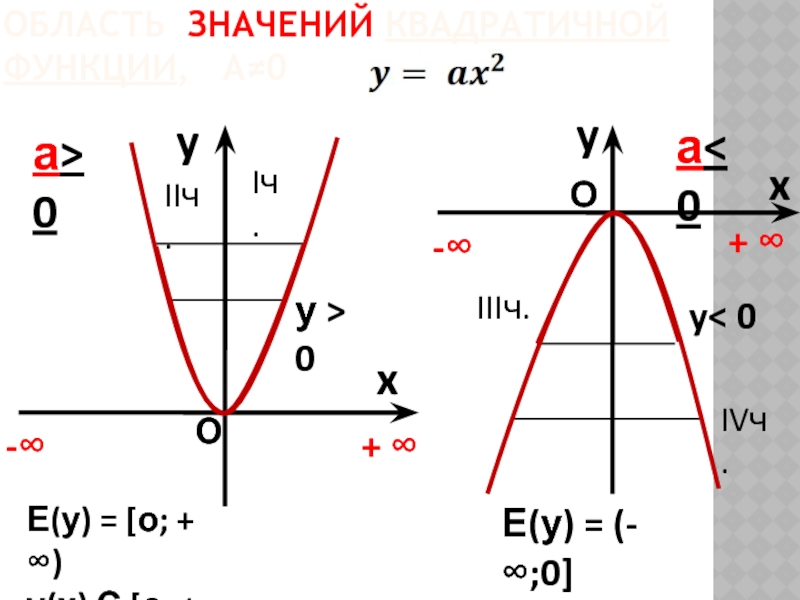
ОБЛАСТЬ ЗНАЧЕНИЙ КВАДРАТИЧНОЙ ФУНКЦИИ, А≠0
y
x
а> 0
y
x
а< 0
Е(у) = [о;
у(х) Є [о; + ∞)
-∞
+ ∞
-∞
+ ∞
О
О
у > 0
y< 0
Iч.
IIIч.
IIч.
IVч.
Е(у) = (-∞;0]
у(х) Є (-∞;0]
Слайд 24
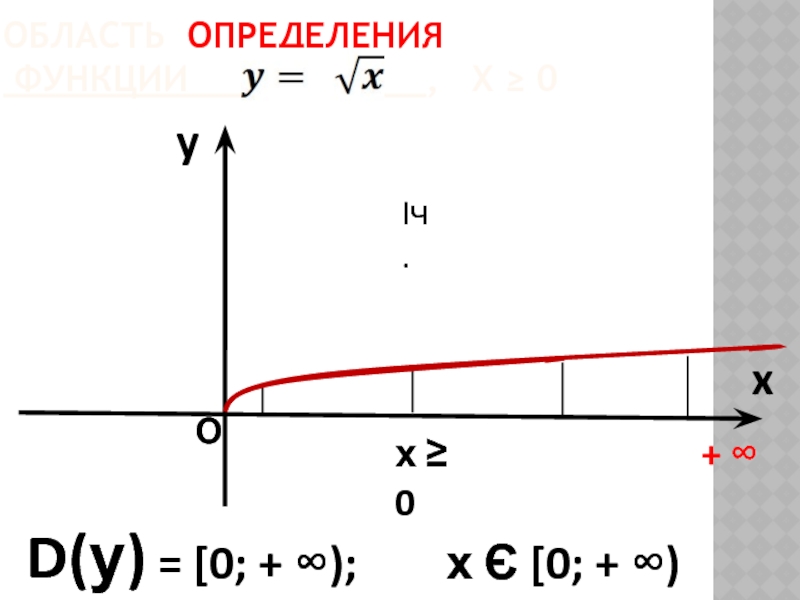
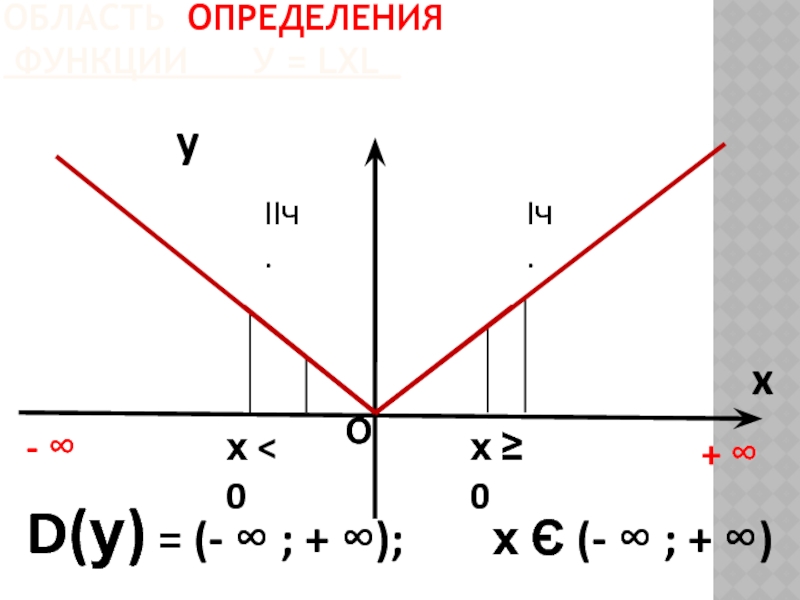
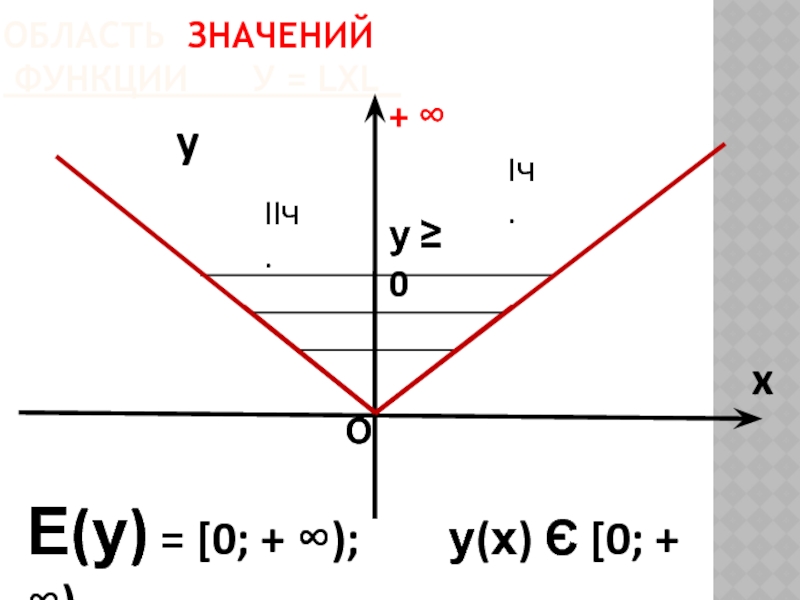
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ
ФУНКЦИИ У = LХL_
y
x
D(у) = (-
+ ∞
О
х < 0
Iч.
х ≥ 0
IIч.
- ∞
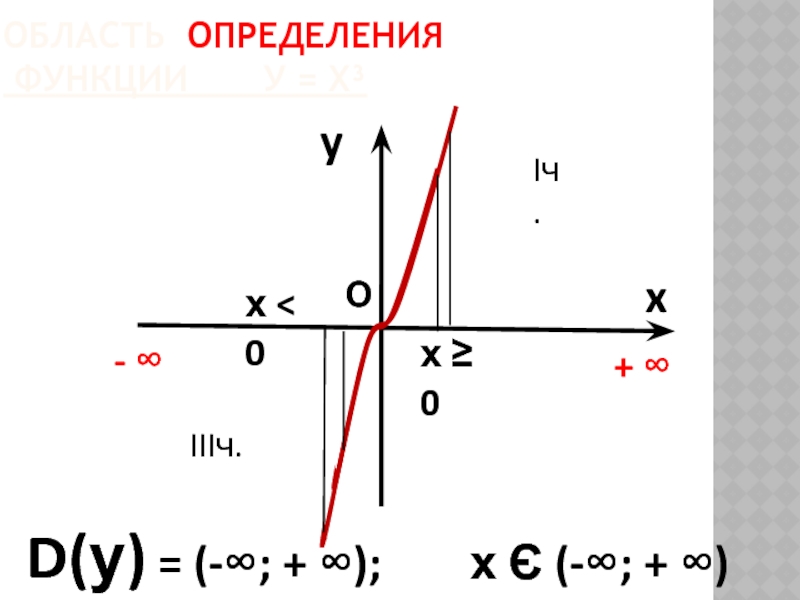
Слайд 26 ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ У = Х³
y
x
D(у) = (-∞; + ∞); х Є (-∞; + ∞)
+ ∞
О
х ≥ 0
Iч.
IIIч.
х < 0
- ∞
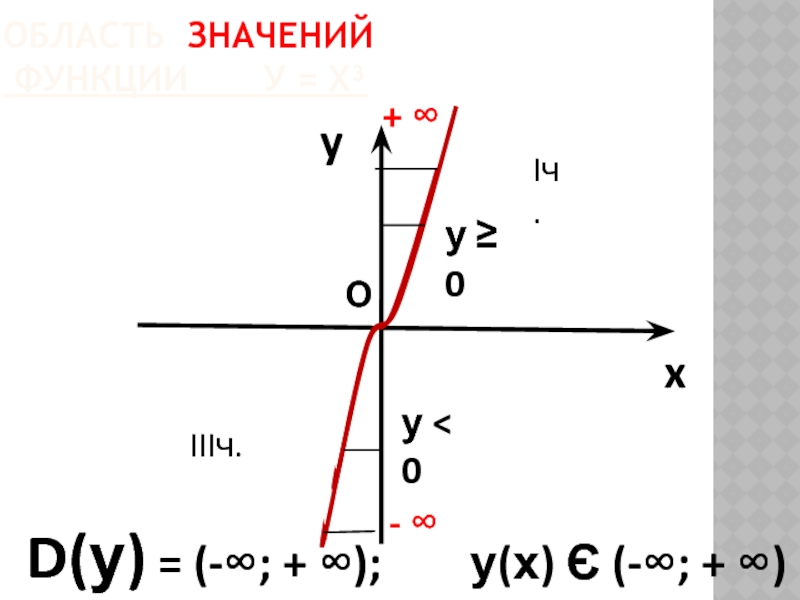
Слайд 27
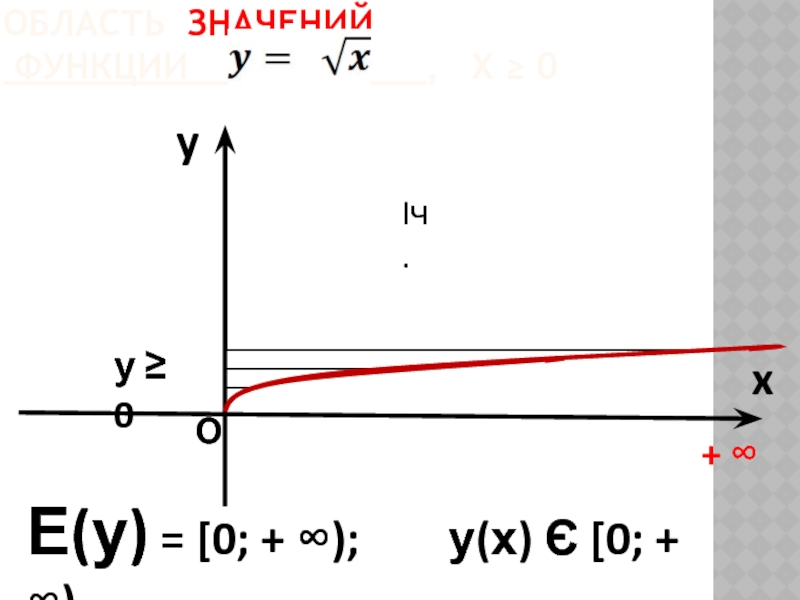
ОБЛАСТЬ ЗНАЧЕНИЙ
ФУНКЦИИ У = Х³
y
x
D(у)
+ ∞
О
у ≥ 0
Iч.
IIIч.
у < 0
- ∞






![Презентация к уроку Область определения и область значения функции 9 класс, алгебра НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ - D(У)-54D(у)= [-5; 4,5] НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ - D(У)-54D(у)= [-5; 4,5]](/img/thumbs/44f1dd9f1b5af7f87c5cbb4f83a68a12-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ - Е(У)-25Е(у)= [-2; 5] НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ - Е(У)-25Е(у)= [-2; 5]](/img/thumbs/56398f347493903d80b135233f39116a-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра ПО ГРАФИКУ ОПРЕДЕЛИТЕ ПРОМЕЖУТОК НА КОТОРОМ ОПРЕДЕЛЕНА ДАННАЯ ФУНКЦИЯ-63D(у)= [-6; 3,5] ПО ГРАФИКУ ОПРЕДЕЛИТЕ ПРОМЕЖУТОК НА КОТОРОМ ОПРЕДЕЛЕНА ДАННАЯ ФУНКЦИЯ-63D(у)= [-6; 3,5]](/img/thumbs/f2c4994b5553eea6052e8e50ca56d24d-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра ПО ГРАФИКУ ОПРЕДЕЛИТЕ ПРОМЕЖУТОК НА КОТОРОМ ОПРЕДЕЛЕНА ДАННАЯ ФУНКЦИЯ-24Е(у)= [-2; 4] ПО ГРАФИКУ ОПРЕДЕЛИТЕ ПРОМЕЖУТОК НА КОТОРОМ ОПРЕДЕЛЕНА ДАННАЯ ФУНКЦИЯ-24Е(у)= [-2; 4]](/img/thumbs/6585eabd5ebf4f99ec907ec061a25149-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ-55D(у)= [-5; 5] НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ-55D(у)= [-5; 5]](/img/thumbs/d15b1d3d9d4cd2067ba7c20b377256dd-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ-26Е(у)= [-2; 6] НАЙДИТЕ ПО ГРАФИКУ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ-26Е(у)= [-2; 6]](/img/thumbs/4e2ea1a70393f165acd79766a68e9ab3-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра -44[ -4;4)3( -1;3]а)б)в)г)д)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ -44[ -4;4)3( -1;3]а)б)в)г)д)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ](/img/thumbs/a1ca6a675f94c1fb5b0557c05e449cec-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ5( -1;5]-34[ -3;4)а)б)в)г)д) НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ5( -1;5]-34[ -3;4)а)б)в)г)д)](/img/thumbs/0c1ec9f605e7fd2b3405f248881d0185-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра -24[ -2;4)4[ -1;4]а)б)в)г)д)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ -24[ -2;4)4[ -1;4]а)б)в)г)д)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ](/img/thumbs/078c1d09c21378fab45414be92a9f182-800x.jpg)
![Презентация к уроку Область определения и область значения функции 9 класс, алгебра б)в)г)-42[ -4;2]2[ -1;2]д)а)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ б)в)г)-42[ -4;2]2[ -1;2]д)а)НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ](/img/thumbs/772624031049b084699fce6344a08c3f-800x.jpg)





