- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теория вероятностей в азартных играх
Содержание
- 1. Презентация по математике на тему Теория вероятностей в азартных играх
- 2. Как все начиналось?Первые задачи вероятностного характера возникли
- 3. Как все начиналось?Французский каноник XIII века Ришар
- 4. Задача о разделе ставкиВ энциклопедии «Сумма арифметики,
- 5. Почти ввел вероятностьКрупный алгебраист XVI века Джероламо
- 6. Почти нормальное распределениеГалилео Галилей написал трактат «О
- 7. Задача об очкахВ XVII веке французский дворянин,
- 8. Задача об очкахПаскаль и Ферма вступили в
- 9. Ввел математическое ожиданиеТематика дискуссии Паскаля и Ферма
- 10. Задача о разорении игрокаВ книге Гюйгенса большое
- 11. Задача о разделе ставокГюйгенс проанализировал и задачу
- 12. Классическое определение вероятностиНа книгу Гюйгенса опирались появившиеся
- 13. Большой вклад в ТВАбрахам де Муавр опубликовал несколько
- 14. СтатистикаК середине XVIII века анализ игр всё ещё
- 15. Применение ТВВ 19 и 20 столетиях теория
- 16. Спасибо за внимание!
Слайд 1Теория вероятностей
в азартных играх
Презентация выполнена учащимися группы 201 Устюжаниным Андреем
Руководитель
Слайд 2Как все начиналось?
Первые задачи вероятностного характера возникли в различных азартных играх
Слово «азар» по-арабски означает «трудный».
Арабы называли азартной игрой комбинацию очков, которая при бросании нескольких костей могла появиться лишь единственным способом.
Например, при бросании двух костей трудным («азар») считалось появление в сумме двух или двенадцати очков.
Древние образцы игральных костей
Слайд 3Как все начиналось?
Французский каноник XIII века Ришар де Фурниваль правильно подсчитал
Это число можно рассматривать как первую числовую меру ожидаемости события, аналогичную вероятности.
Ришар де Фурниваль
1201- 1259
французский священнослужитель, поэт, медик.
Лесная дева с единорогом
Бестиарий любви
Слайд 4Задача о разделе ставки
В энциклопедии «Сумма арифметики, геометрии, отношений и пропорций»
Решение зависит от того, что понимать под «справедливым» разделом; сам Пачоли предложил делить пропорционально набранным очкам; позднее его решение было признано ошибочным.
Фра Лука Бартоломео де Пачоли
1447-1517 итальянский математик
Слайд 5Почти ввел вероятность
Крупный алгебраист XVI века Джероламо Кардано посвятил анализу игры
Кардано отметил, что реальное количество исследуемых событий может при небольшом числе игр сильно отличаться от теоретического, но чем больше игр в серии, тем доля этого различия меньше.
По существу, Кардано близко подошёл к понятию вероятности:
Джероламо Кардано
1501-1576
итальянский математик, инженер, философ,
Слайд 6
Почти нормальное распределение
Галилео Галилей написал трактат «О выходе очков при игре
В своей главной книге «Диалог о двух главнейших системах мира, птоломеевой и коперниковой» Галилей указал на возможность оценки погрешности астрономических и иных измерений, причём заявил, что малые ошибки измерения вероятнее, чем большие, отклонения в обе стороны равновероятны, а средний результат должен быть близок к истинному значению измеряемой величины.
Галиле́о Галиле́й
1564-1642 итальянский физик, механик, астроном, философ, математик
Слайд 7Задача об очках
В XVII веке французский дворянин, господин де Мере, был
Де Мере обратился к Паскалю по поводу «задачи об очках»: сколько раз нужно бросать две кости, чтобы было выгодно ставить на одновременное выпадение хотя бы раз двух шестёрок?
Распределение суммы очков после бросания двух костей
Слайд 8Задача об очках
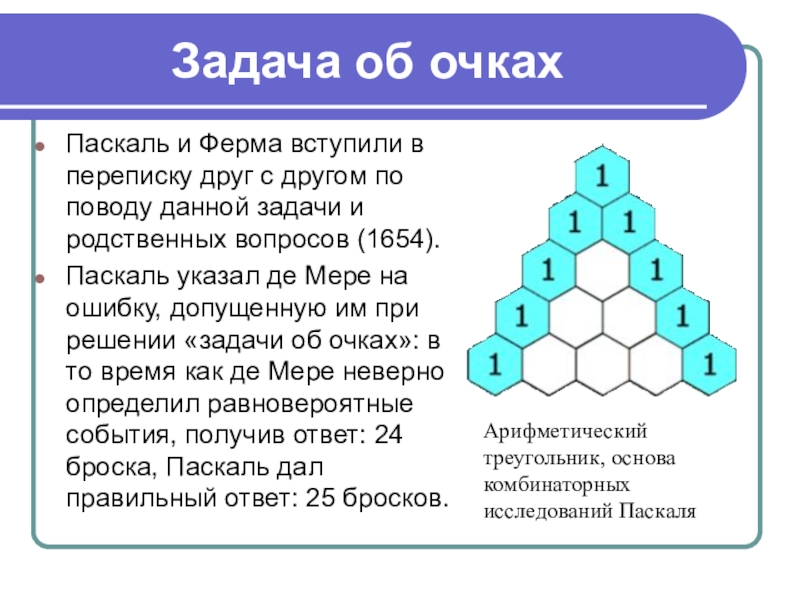
Паскаль и Ферма вступили в переписку друг с другом
Паскаль указал де Мере на ошибку, допущенную им при решении «задачи об очках»: в то время как де Мере неверно определил равновероятные события, получив ответ: 24 броска, Паскаль дал правильный ответ: 25 бросков.
Арифметический треугольник, основа комбинаторных исследований Паскаля
Слайд 9Ввел математическое ожидание
Тематика дискуссии Паскаля и Ферма стала известна Христиану Гюйгенсу, который
Главным достижением нидерландского учёного стало введение понятия математического ожидания.
Гюйгенс также указал классический способ его подсчёта.
Христиа́н Гю́йгенс ван Зёйлихем
1629-1695 нидерландский механик, физик, математик, астроном и изобретатель
Слайд 10Задача о разорении игрока
В книге Гюйгенса большое число задач, некоторые с
Из последних особый интерес и оживлённое обсуждение вызвала «задача о разорении игрока». В несколько обобщённом виде она формулируется так: у игроков A и B есть a и b монет соответственно, в каждой игре выигрывается одна монета, вероятность выигрыша A в каждой игре равна p, требуется найти вероятность полного его разорения.
Полное общее решение «задачи о разорении» дал Абрахам де Муавр полвека спустя (1711).
В наши дни вероятностная схема «задачи о разорении» используется при решении многих задач типа «случайное блуждание».
Слайд 11Задача о разделе ставок
Гюйгенс проанализировал и задачу о разделе ставки, дав
Он также впервые применил вероятностные методы к демографической статистике и показал, как рассчитать среднюю продолжительность жизни.
Карманные механические часы, изобретение Гюйгенса
Слайд 12Классическое определение вероятности
На книгу Гюйгенса опирались появившиеся в начале XVIII века
Трактат стал первым систематическим изложением теории вероятностей. В этой книге автор привёл, в частности, классическое определение вероятности события
Трактат «Искусство предположений»
Слайд 13Большой вклад в ТВ
Абрахам де Муавр опубликовал несколько работ: статья «Об измерении
В этом трактате Муавр не только полностью решил «задачу о разорении игрока», но и оценил для неё среднюю продолжительность игры и вероятности выигрыша за заданное число игр для каждого игрока
Абрахам де Муавр
1667-1754
английский математик