“Да пусть познания не гладок
Но знаем мы со школьных лет,
Загадок больше, чем разгадок
И поискам предела нет!”.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку квадратичная функция
Содержание
- 1. Презентация к уроку квадратичная функция
- 2. Тема урокаУчитель математики: Маахунова Б.А.у = ах2+вх+сФункция
- 3. ТренингФормирование групп
- 4. Напишите уравнение функции ?Укажите расположение графика функции на координатном плоскости
- 5. Проверка д/з№268,
- 6. функция вида у(х)= ах2 + в
- 7. Внимание! Вопрос! Какие из данных функций являются
- 8. Свойства функции у=ах21)Графиком является парабола.Ветви параболыОсь
- 9. 2)Промежутки монотонности у=ах2 (возрастания и убывания) у(х) возрастает приа>0а
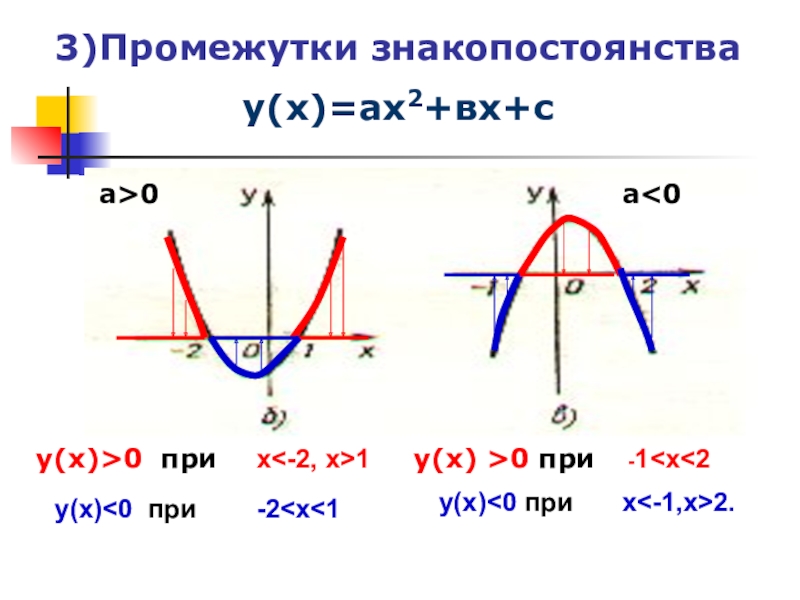
- 10. 3)Промежутки знакопостоянствау(х)=ах2+вх+су(х)>0 при а>0у(х) >0 приа
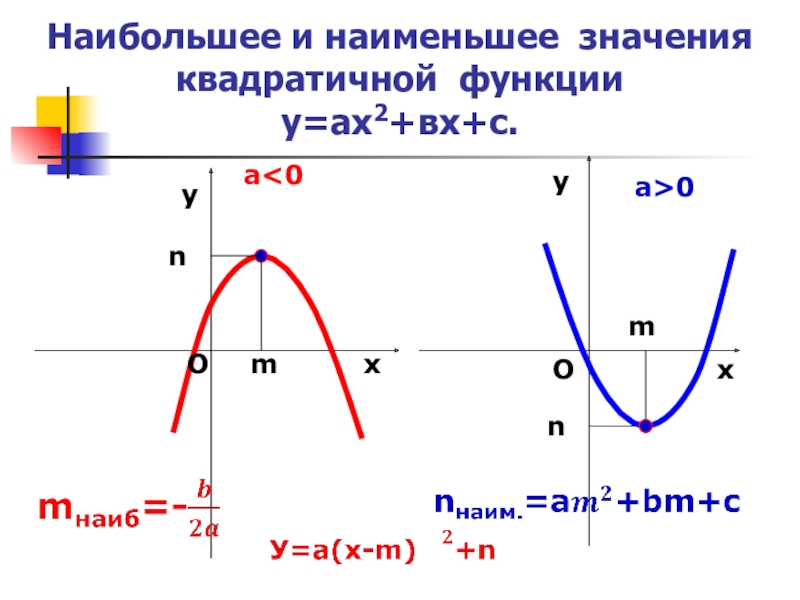
- 11. Наибольшее и наименьшее значения квадратичной функции у=ах2+вх+с.mmххnnуу а0 ОО
- 12. Задание №1. математический диктант на 3ед. влево и
- 13. Ответы б) у = (х-4)2 –
- 14. Работа в пареа) у = х2 – 4.у=0б) у = х2 – х,у=0
- 15. Задание №2Найти координаты вершины параболыа) у(х)=х2-4х-5,б) у(х)=-х2-2х+5.
- 16. Внимание! Правильные решения!а) у(х)=х2-4х-5а=1,в=-4,n=n(2)=22-4*2-5==4-8-5=-4-5=-9,(2;-9)-координаты вершины параболыб)
- 17. Работа в группах1. Найти нули квадратичной функции(если они существуют).у=х2+5х+6;у=х2- 5х+4;2. Найти координаты вершины параболы.у=х2-10х+9;у=х2-6х+8.
- 18. Правильные решения№1. 1.
- 19. Правильные решения№3.
- 20. Построить график функции у=х2-4х+3. n=у(2)=22-4*2+3=4-8+3=7-8=-1.(2;-1)-координаты вершины параболы.Построим точку (2;-1)
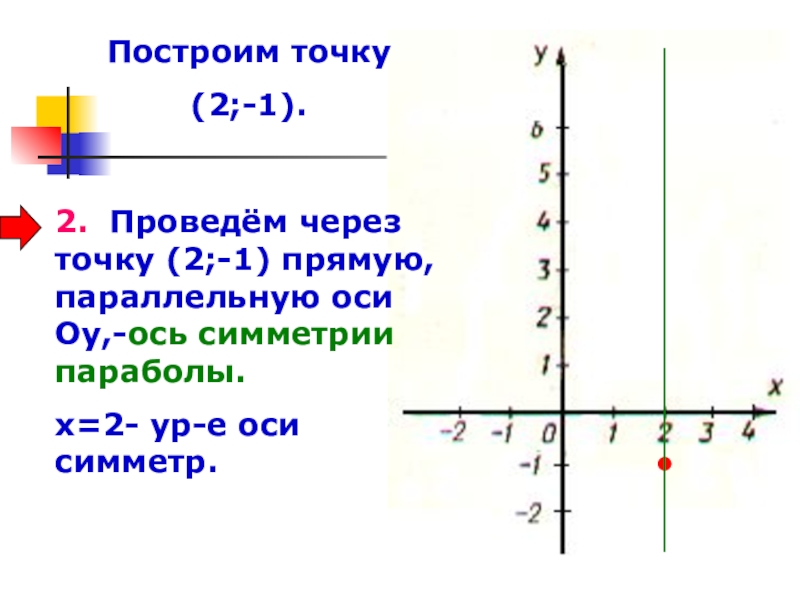
- 21. Построим точку (2;-1).2. Проведём через точку (2;-1) прямую, параллельную оси Оу,-ось симметрии параболы.х=2- ур-е оси симметр.
- 22. Найдём нули функции у=х2-4х+3, а для параболы-
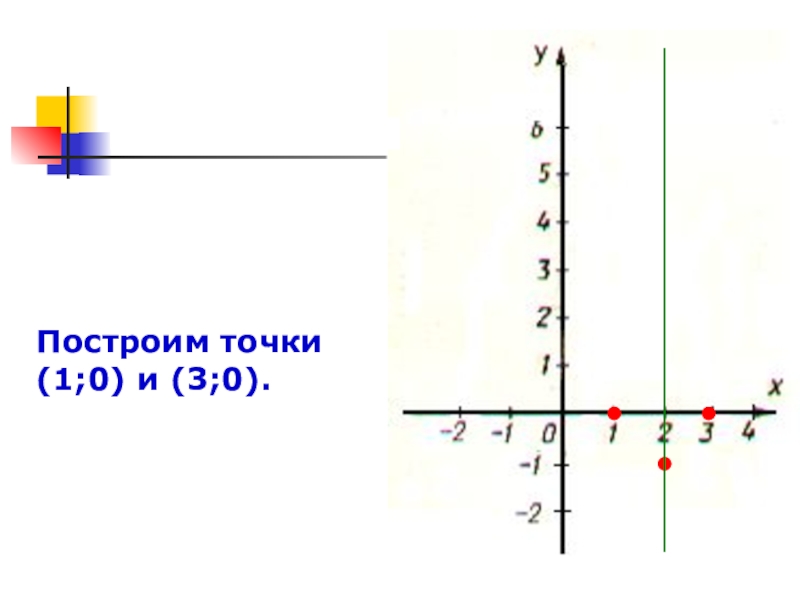
- 23. Построим точки (1;0) и (3;0).
- 24. Возьмём две точки на оси Ох, симметричные
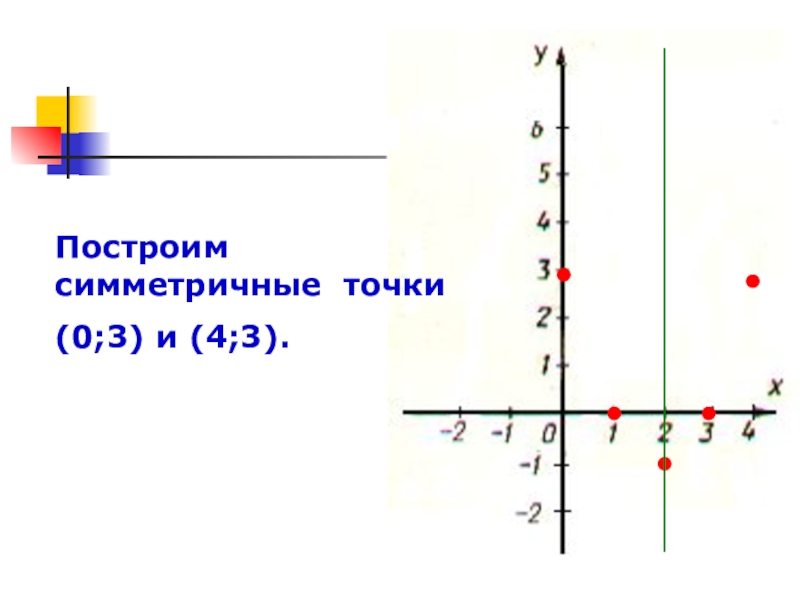
- 25. Построим симметричные точки (0;3) и (4;3).
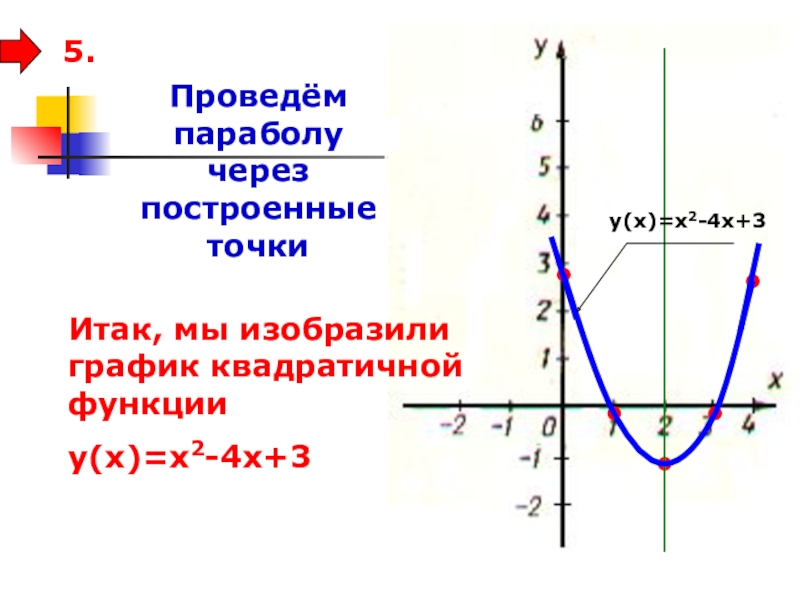
- 26. 5. Проведём параболу через построенные точкиИтак, мы изобразили график квадратичной функции у(х)=х2-4х+3у(х)=х2-4х+3
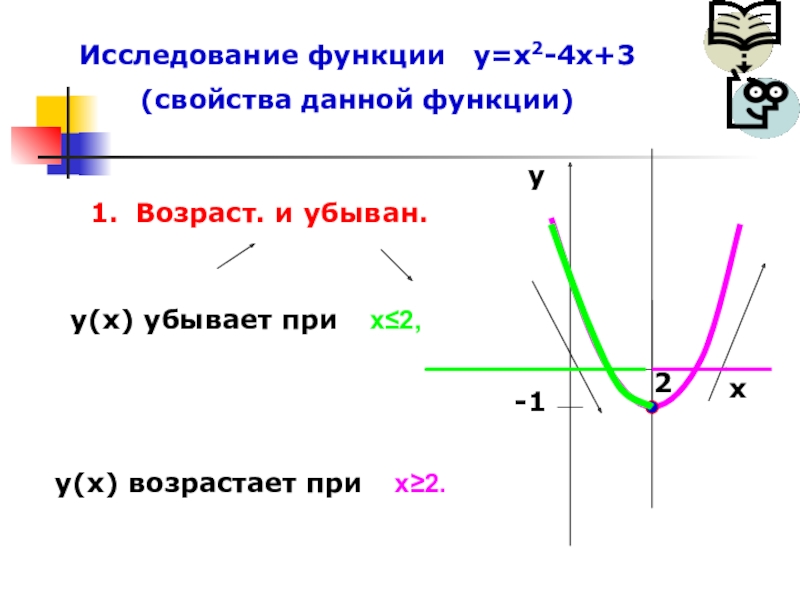
- 27. Исследование функции у=х2-4х+3(свойства данной функции)ху2-1 у(х) убывает приу(х) возрастает приВозраст. и убыван.х≤2,х≥2.
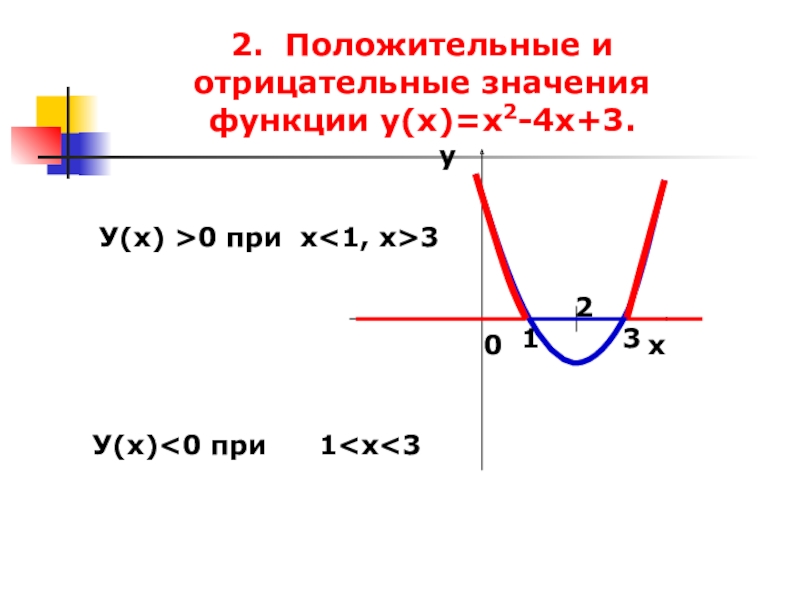
- 28. 2. Положительные и отрицательные значения функции у(х)=х2-4х+3.1 2 ху03У(х) >0 приУ(х)
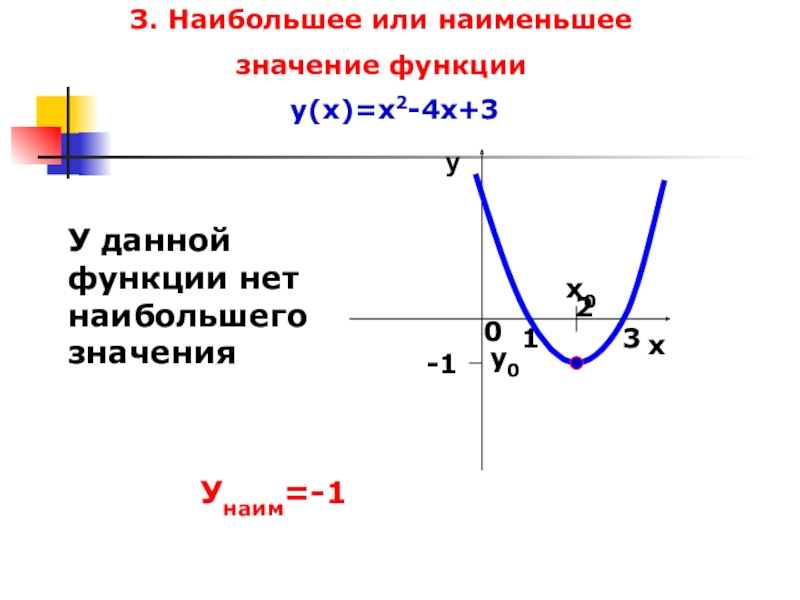
- 29. З. Наибольшее или наименьшеезначение функции у(х)=х2-4х+31 2 х03х0у0-1У данной функции нет наибольшего значенияУнаим=-1у
- 30. Слайд 30
- 31. №276
- 32. АЛГОРИТМ построения графика квадратичной функции у=ах2+вх+сОпределить
Тема урокаУчитель математики: Маахунова Б.А.у = ах2+вх+сФункция
Слайд 6функция вида
у(х)= ах2 + в х + с,
где
а, в, с
– заданные числа, а≠0
х – независимая переменная
у – зависимая переменная
х – независимая переменная
у – зависимая переменная
Квадратичной функцией называется
(функция)
(аргумент)
Слайд 7Внимание! Вопрос!
Какие из данных функций являются квадратичными? ( укажите номер).
у
= 3х2 + х + 2,
у = 4х2 – 1,
у = 6х + 1,
у = - 7х2,
у = х3 + 7х – 5,
у = - 8х2 + 3х.
у = 4х2 – 1,
у = 6х + 1,
у = - 7х2,
у = х3 + 7х – 5,
у = - 8х2 + 3х.
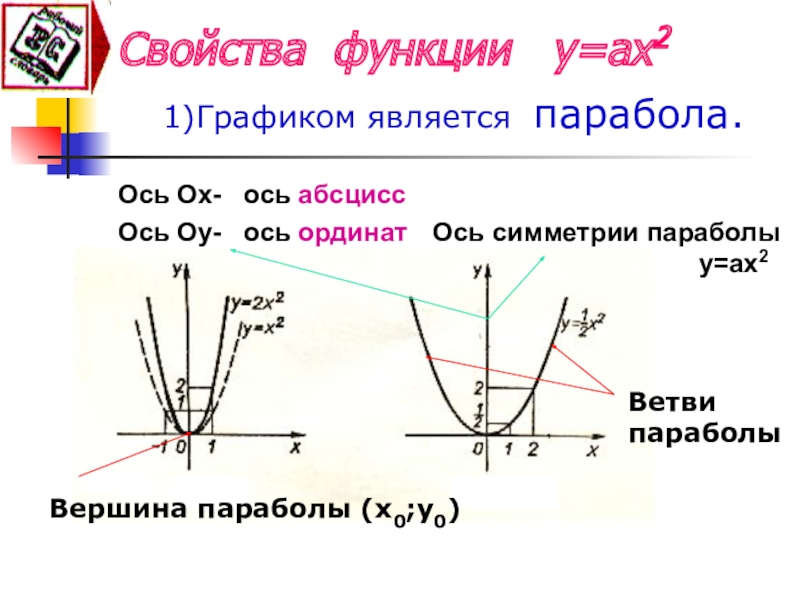
Слайд 8Свойства функции у=ах2
1)Графиком является парабола.
Ветви параболы
Ось Ох-
ось абсцисс
Ось Оу-
ось ординат
Вершина
параболы (х0;у0)
Ось симметрии параболы
у=ах2
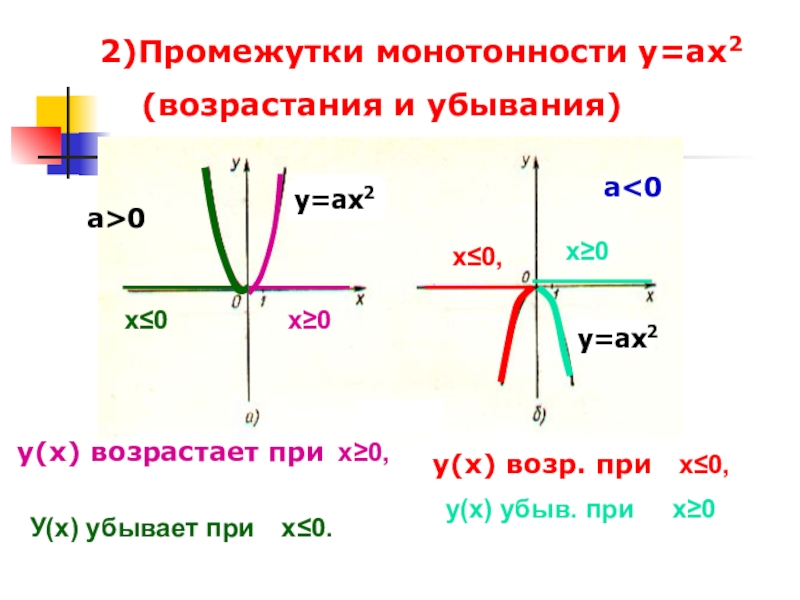
Слайд 92)Промежутки монотонности у=ах2
(возрастания и убывания)
у(х) возрастает при
а>0
а
при
У(х) убывает при
у(х) убыв. при
х≥0,
х≥0
х≤0
х≤0.
х≤0,
х≥0
х≥0
х≤0,
у=ах2
у=ах2
Слайд 12Задание №1.
математический диктант
на 3ед. влево и на 2 ед. вверх
на 4ед.
вправо и на 3ед.вниз
на 5ед. влево и на 5 ед. вниз
на 6ед. вправо и на 2ед. вверх
на 7ед. влево и на 1ед. вниз
на 5ед. влево и на 5 ед. вниз
на 6ед. вправо и на 2ед. вверх
на 7ед. влево и на 1ед. вниз
Слайд 16Внимание!
Правильные решения!
а) у(х)=х2-4х-5
а=1,в=-4,
n=n(2)=22-4*2-5=
=4-8-5=-4-5=-9,
(2;-9)-координаты вершины параболы
б) у(х)=-х2-2х+5,
а=-1, в=-2,
n=n(-1)=-(-1)2-2*
(-1)+5=-1+2+5=-1+ +7=6;
(-1;6)-коорд.
верш. параб.
(-1;6)-коорд.
верш. параб.
Слайд 17Работа в группах
1. Найти нули квадратичной функции
(если они существуют).
у=х2+5х+6;
у=х2- 5х+4;
2. Найти
координаты вершины параболы.
у=х2-10х+9;
у=х2-6х+8.
Слайд 18Правильные решения
№1.
1.
у=х2+5х+6;
у=0 , х2+5х+6=0;
D=52- 4*1*6=25-24=1;
Ответ: х1=-2, х2=-3.
у=0 , х2+5х+6=0;
D=52- 4*1*6=25-24=1;
Ответ: х1=-2, х2=-3.
№-2.
1. у=х2-5х+4;
у=0, х2-5х+4=0;
х1+х2=5, х1=4,
х1*х2=4; х2=1.
(по теореме,обратной теореме Виета)
Ответ: х1=4, х2=1
Слайд 19Правильные решения
№3.
№4.
2.
у=х2-10х+9 (m;n)-?
n=52-10*5+9=25-50+9= =-25+9=-16;
(5;-16)
Ответ: (5;-16).
2. у=х2-6х+8, (m;n)-?
n=32-6*3+8=9-18+8= =9-10=-1;
(3;-1)
Ответ: (3;-1).
Слайд 20Построить график функции у=х2-4х+3.
n=у(2)=22-4*2+3=4-8+3=7-8=-1.
(2;-1)-координаты вершины параболы.
Построим точку (2;-1)
Слайд 21Построим точку
(2;-1).
2. Проведём через точку (2;-1) прямую, параллельную оси Оу,-ось
симметрии параболы.
х=2- ур-е оси симметр.
х=2- ур-е оси симметр.
Слайд 22
Найдём нули функции у=х2-4х+3, а для параболы- точки пересечения с осью
Ох.
у=0 х2-4х+3=0
х1+х2=4,
х1*х2=3.
х1=1,
х2=3.
нули функции
(1;0),(3;0)-коорд. точек пересеч. параболы с осью Ох.
Построим точки (1;0) и (3;0).
3.
Слайд 24
Возьмём две точки на оси Ох, симметричные относительно точки х=2,
например,
х3=0,х4=4.
Вычислим значения функции
у=х2-4х+3 в этих точках:
у(0)= у(4)=02-4*0+3=3
Получим симметр.точки (0;3),(4;3).
Построим их.
х3=0,х4=4.
Вычислим значения функции
у=х2-4х+3 в этих точках:
у(0)= у(4)=02-4*0+3=3
Получим симметр.точки (0;3),(4;3).
Построим их.
4.
Слайд 265.
Проведём параболу через построенные точки
Итак, мы изобразили график квадратичной функции
у(х)=х2-4х+3
у(х)=х2-4х+3
Слайд 27Исследование функции у=х2-4х+3
(свойства данной функции)
х
у
2
-1
у(х) убывает при
у(х) возрастает при
Возраст.
и убыван.
х≤2,
х≥2.
Слайд 282. Положительные и отрицательные значения функции у(х)=х2-4х+3.
1
2
х
у
0
3
У(х) >0
при
У(х)<0 при
х<1, х>3
1<х<3
Слайд 29З. Наибольшее или наименьшее
значение функции
у(х)=х2-4х+3
1
2
х
0
3
х0
у0
-1
У
данной функции нет наибольшего значения
Унаим=-1
у
Слайд 32АЛГОРИТМ
построения графика квадратичной функции у=ах2+вх+с
Определить направление ветвей.
1.Вершина параболы (х
0,у 0)
х0=-в/2а,у0=у(х0).
2.Ось симметрии.
3.Нули функции, если они есть.
4.Симметричные точки.
5.Провести через построенные точки параболу.
х0=-в/2а,у0=у(х0).
2.Ось симметрии.
3.Нули функции, если они есть.
4.Симметричные точки.
5.Провести через построенные точки параболу.
