- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Функция y=tgx и ее свойства
Содержание
- 1. Презентация к уроку Функция y=tgx и ее свойства
- 2. Функция y=tg x и её свойства1. Обл.
- 3. Функция y=tg x возрастает на промежутке2. Т.
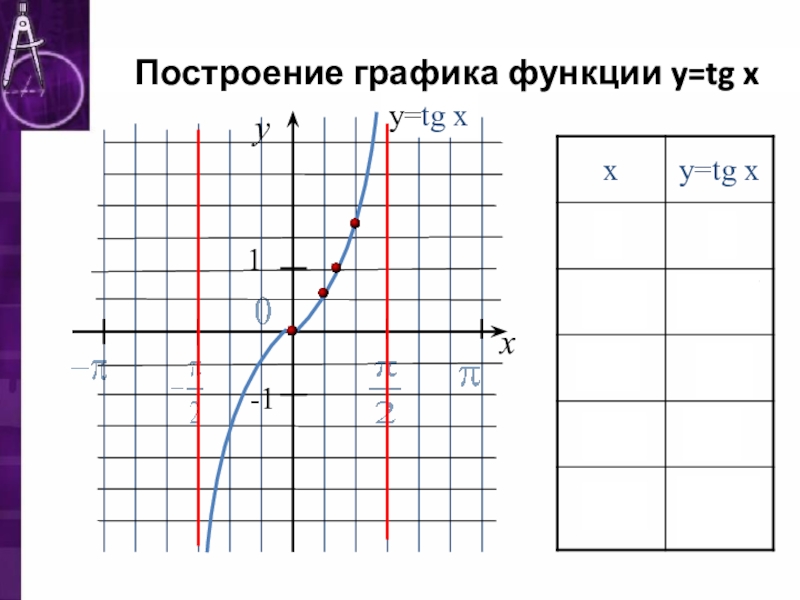
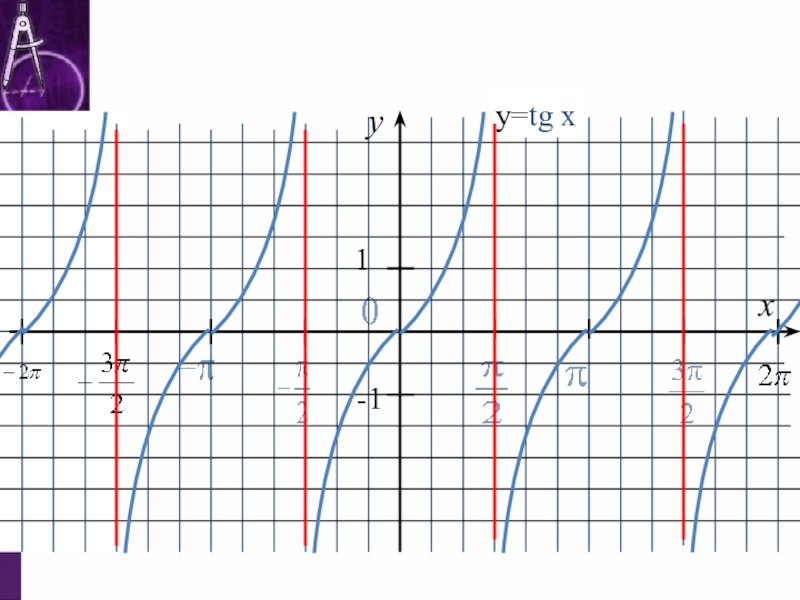
- 4. Построение графика функции y=tg x yx1-1у=tg x
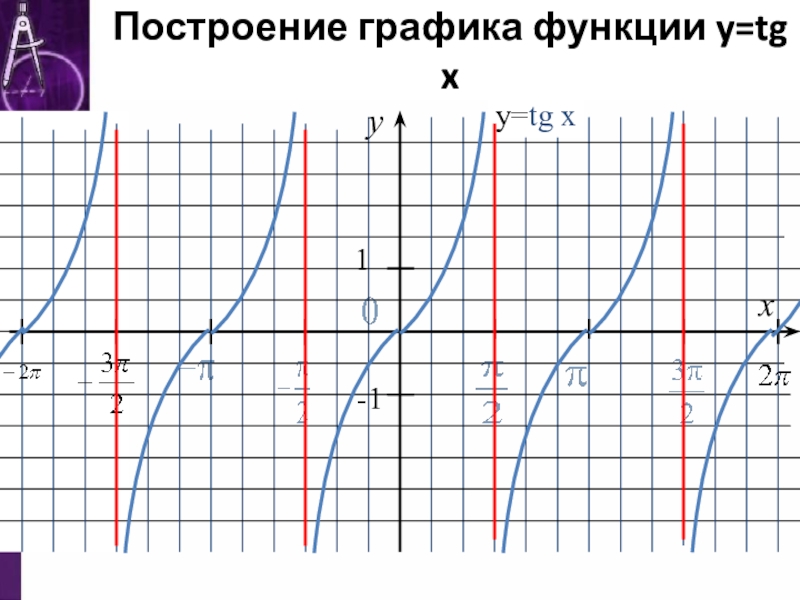
- 5. Построение графика функции y=tg xyx1-1у=tg x
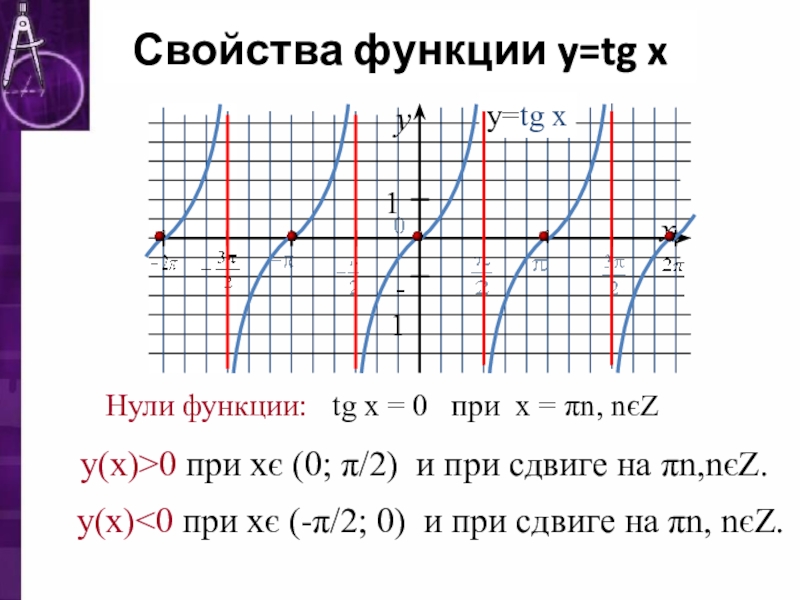
- 6. Свойства функции y=tg x Нули функции: tg
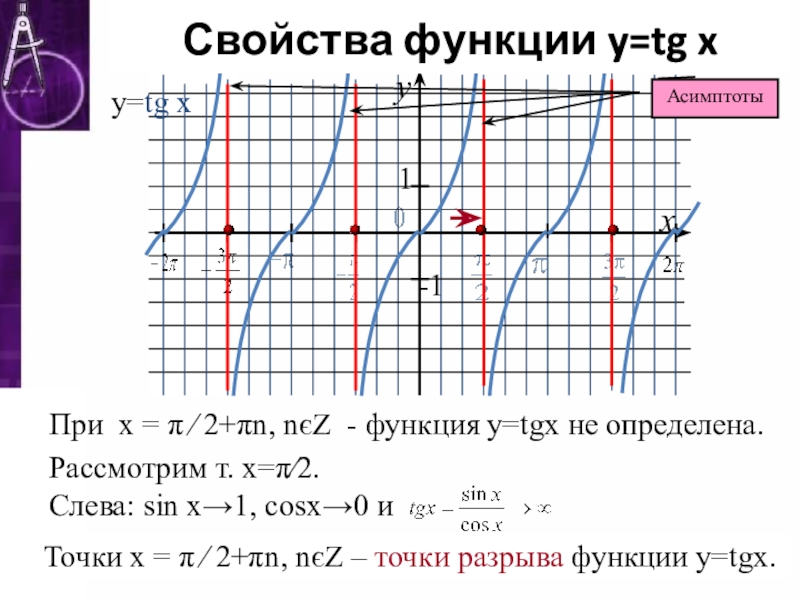
- 7. Свойства функции y=tg x у=tg xПри х
- 8. Свойства функции y=tgx1. Обл. определения:
- 9. Задача №1.Найти все корни уравнения tgx=2 принадлежащих
- 10. Задача №2.Найти все решения неравенства tgx ≤
- 11. yx1-1у=tg x
Слайд 2Функция y=tg x и её свойства
1. Обл. определения:
2. Множество значений функции: уєR.
3. Периодическая, Т= π.
4. Нечётная функция.
хє[0;π/2)
Слайд 3Функция y=tg x возрастает на промежутке
2. Т. к. функция у=sin x
промежутке, то sin х1< sin x2.
3. Т. к. функция у=соs x убывает на данном
промежутке, то соs х1> соs x2 и
(1)
(2)
4.Умножим нер-во (1) на нер-во (2) :
, т. е. tg x1< tg x2 .
Слайд 6Свойства функции y=tg x
Нули функции:
tg х = 0
у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ.
у(х)<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ.
Слайд 7
Свойства функции y=tg x
у=tg x
При х = π ∕ 2+πn,
Рассмотрим т. х=π∕2.
Слева: sіn x→1, сosx→0 и
Точки х = π ∕ 2+πn, nєZ – точки разрыва функции у=tgx.
Слайд 8Свойства функции y=tgx
1. Обл. определения:
2. Множество значений функции: уєR.
3. Периодическая, Т= π.
4. Нечётная функция.
5. Возрастает на всей области определения.
6. Нули функции у (х) = 0 при х = πn, nєZ.
7. у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ.
8. у(х)<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ.
9. При х = π ∕ 2+πn, nєZ - функция у=tgx не определена. Имеет точки разрыва графика и асимптоты.
Слайд 9
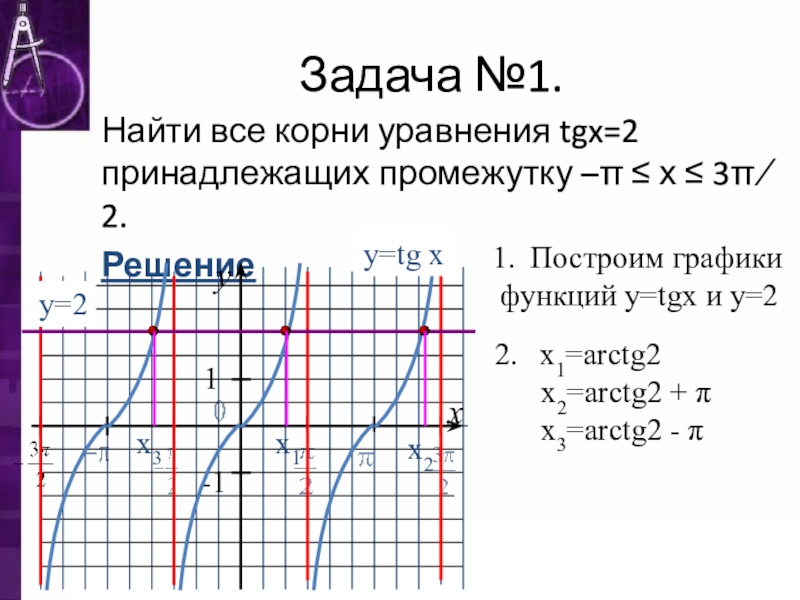
Задача №1.
Найти все корни уравнения tgx=2 принадлежащих промежутку –π ≤ х
Решение
у=tg x
у=2
Построим графики
функций у=tgx и у=2
х1=arctg2
х2=arctg2 + π
х3=arctg2 - π
х1
х3
х2
Слайд 10
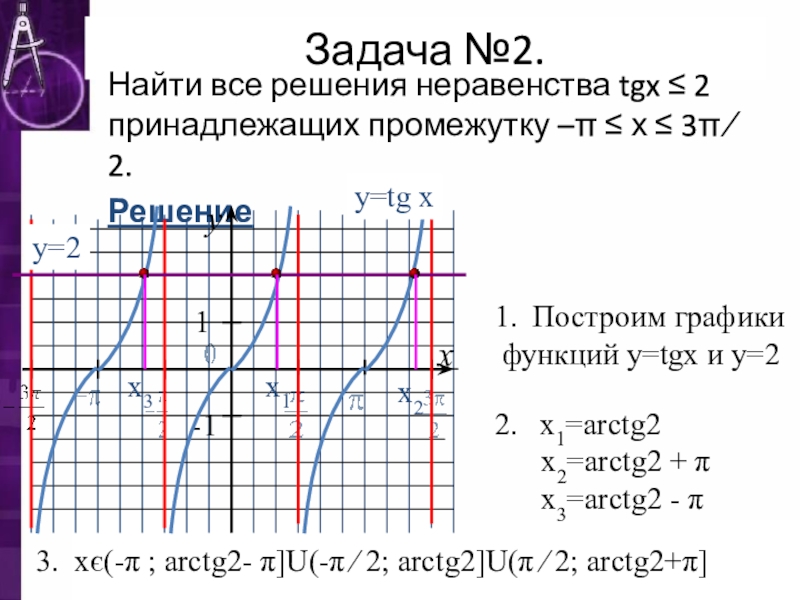
Задача №2.
Найти все решения неравенства tgx ≤ 2 принадлежащих промежутку –π
Решение
у=tg x
у=2
Построим графики
функций у=tgx и у=2
х1=arctg2
х2=arctg2 + π
х3=arctg2 - π
х1
х3
х2
3. хє(-π ; arctg2- π]U(-π ∕ 2; arctg2]U(π ∕ 2; arctg2+π]