график.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
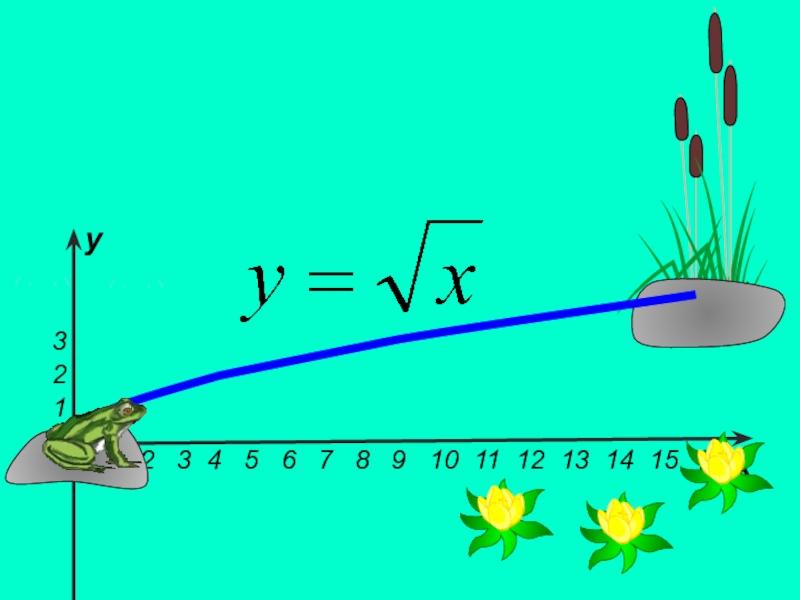
Презентация, доклад к уроку Функция арифметического квадратного корня, её свойства и график.
Содержание
- 1. Презентация к уроку Функция арифметического квадратного корня, её свойства и график.
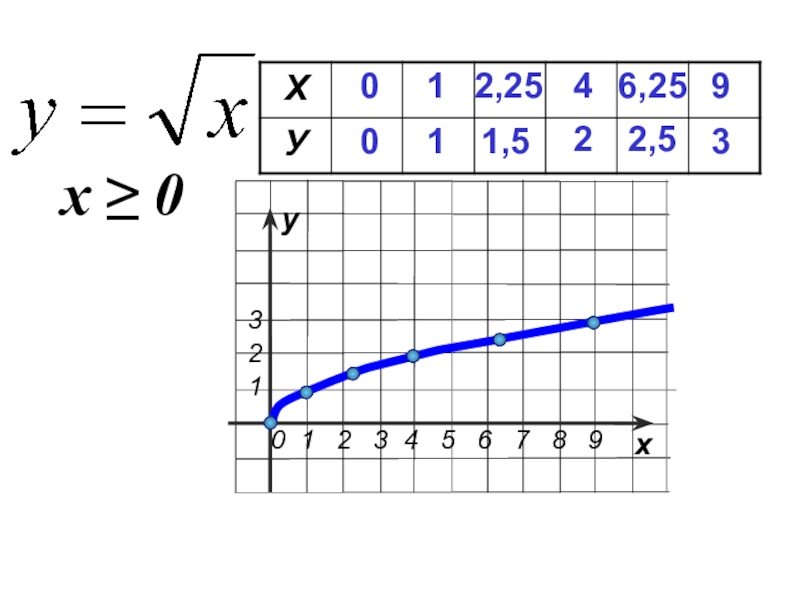
- 2. Слайд 2
- 3. 0 0 1 1 4 26,252,5 9 32,251,5х ≥ 0
- 4. 7. Непрерывна. Функция возрастает при Функция
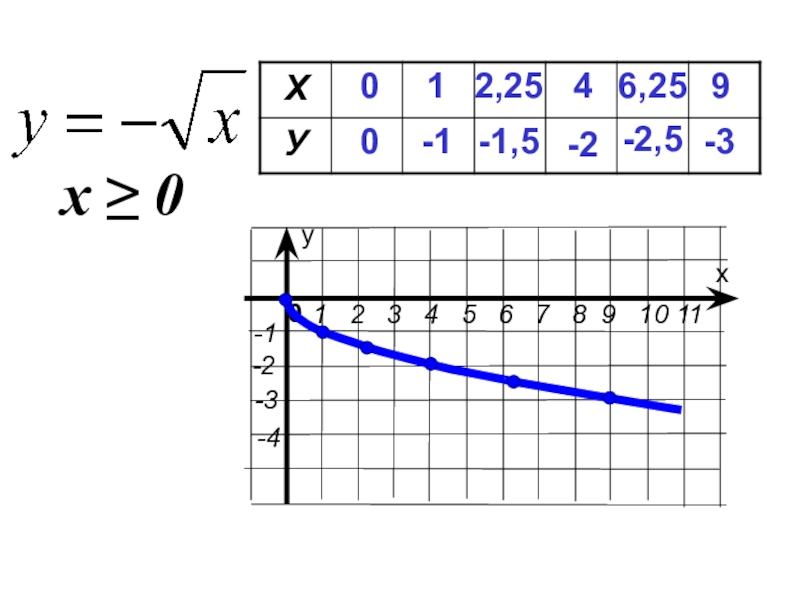
- 5. 0 0 1 -1 4 -26,25-2,5 9 -32,25-1,5х ≥ 0
- 6. 7. Непрерывна. Функция убывает
- 7. хуПостройте график функции:х=3у=41.Вспомогательная система координат:2. Привязываем к
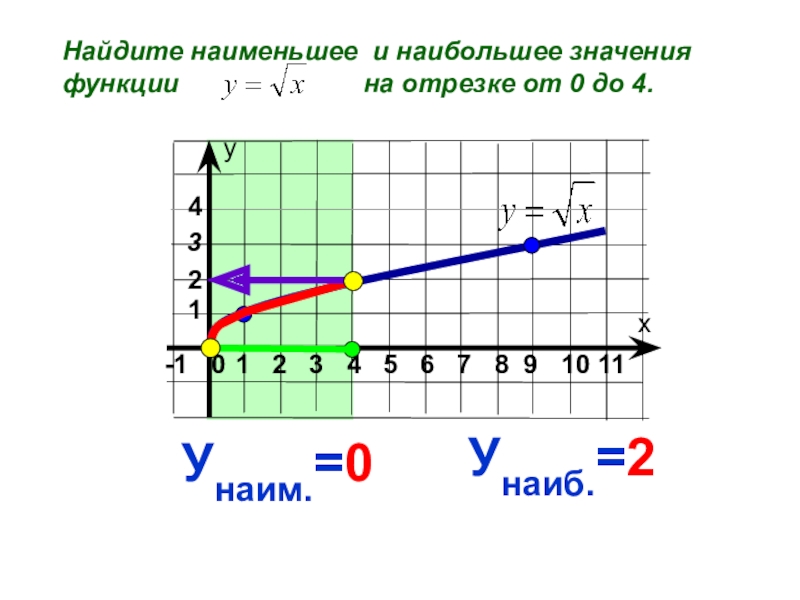
- 8. Найдите наименьшее и наибольшее значения
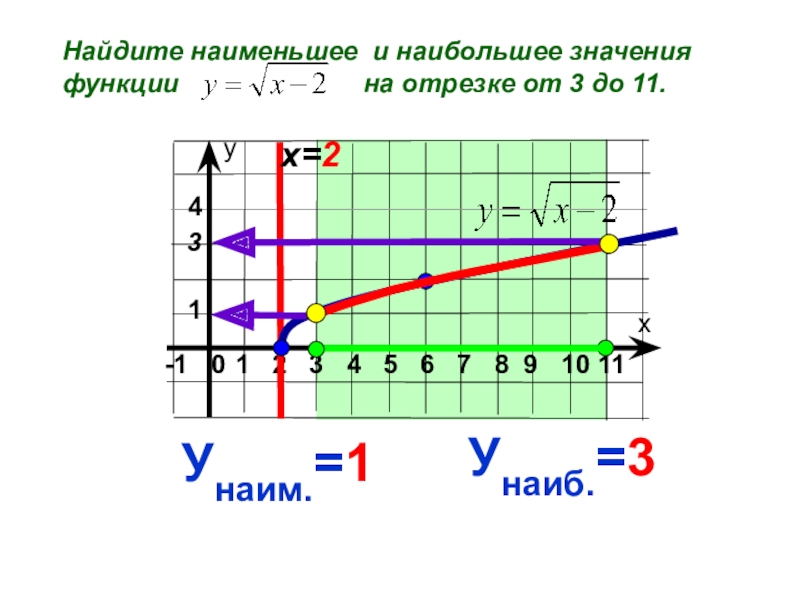
- 9. Найдите наименьшее и наибольшее значения
- 10. у=√х√х=х-6Построим в одной системе координат графики функций:у=х-610
- 11. Построим в одной системе координат графики функций:хуРешить
- 12. f(x)=Постройте график функциии опишите её свойства.√x+3,если -3≤х≤12(х-1)²,если 1
- 13. ухf(x)=√x+3,если -3≤х≤12(х-1)²,если 1
- 14. Функция возрастает при Функция ограничена
0 0 1 1 4 26,252,5 9 32,251,5х ≥ 0
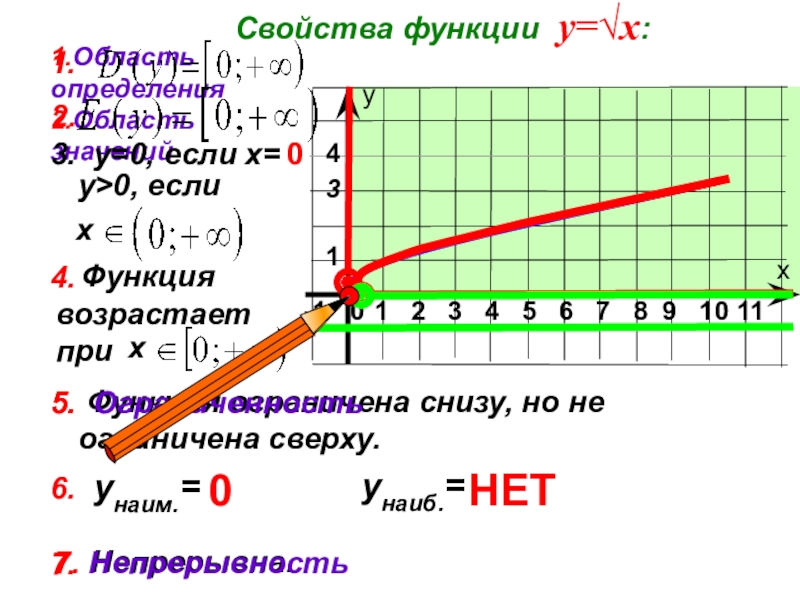
Слайд 4
7.
Непрерывна.
Функция возрастает при
Функция ограничена снизу,
но не ограничена сверху.
Свойства функции у=√х:
1.Область определения
2.Область значений
3. у=0, если х=
0
у>0, если
4.
5. Ограниченность
1.
2.
5.
6. унаим.=
унаиб.=
НЕТ
0
7. Непрерывность
Слайд 6
7.
Непрерывна.
Функция убывает при
Функция
ограничена сверху, и не ограничена снизу.
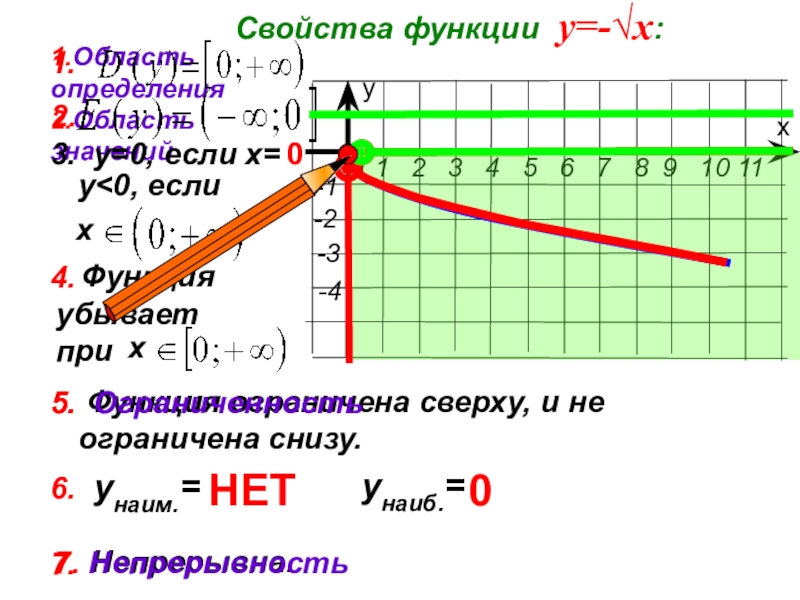
Свойства функции у=-√х:
1.Область определения
2.Область значений
3. у=0, если х=
0
у<0, если
4.
5. Ограниченность
1.
2.
5.
6. унаим.=
унаиб.=
0
НЕТ
7. Непрерывность
Слайд 7х
у
Постройте график функции:
х=3
у=4
1.Вспомогательная система координат:
2. Привязываем к ней график функции
х= 3
у= 4
0
0
1
1
4
2
Слайд 10у=√х
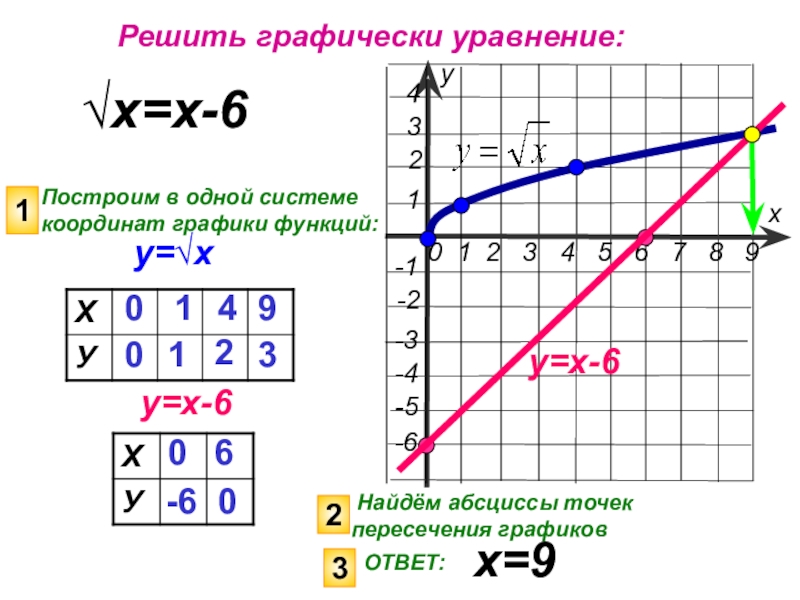
√х=х-6
Построим в одной системе координат графики функций:
у=х-6
1
0
-6
6
0
2
Найдём абсциссы точек
пересечения графиков
3
ОТВЕТ:
х=9
Решить графически уравнение:
у=х-6
0
0
1
1
4
9
2
3
Слайд 11Построим в одной системе координат графики функций:
х
у
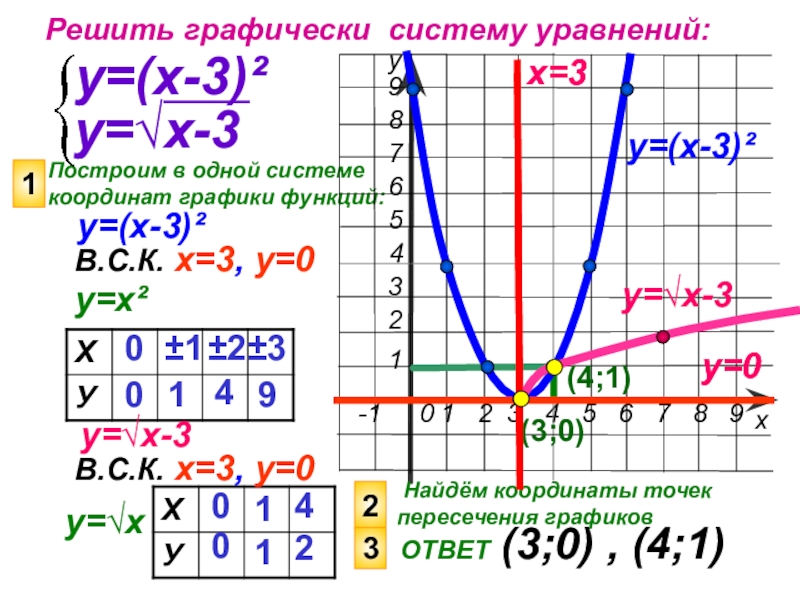
Решить графически систему уравнений:
у=(х-3)²
у=(х-3)²
1
у=(х-3)²
у=√х-3
Найдём координаты точек пересечения графиков
ОТВЕТ
(3;0) , (4;1)
х=3
у=0
(3;0)
0
0
±1
1
±2
±3
4
9
у=х²
В.С.К. х=3, у=0
0
0
1
4
2
В.С.К. х=3, у=0
у=√х
1
(4;1)
х=3
у=0
у=√х-3
2
3
Слайд 13
у
х
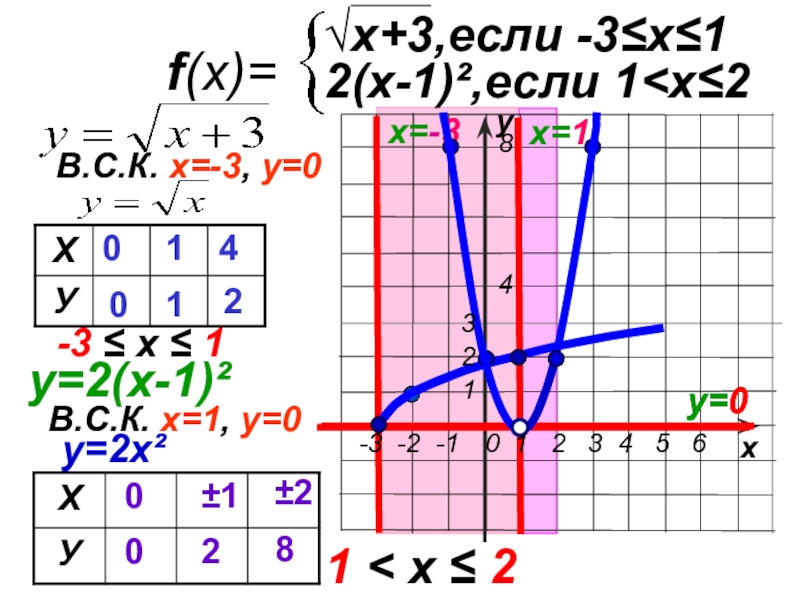
f(x)=
√x+3,если -3≤х≤1
2(х-1)²,если 1
≤ х ≤ 1
В.С.К. х=1, у=0
х=1
у=0
у=2х²
0
0
±1
2
±2
8
1 < х ≤ 2
Слайд 14
Функция возрастает при
Функция ограничена сверху и снизу.
1
х
у
0
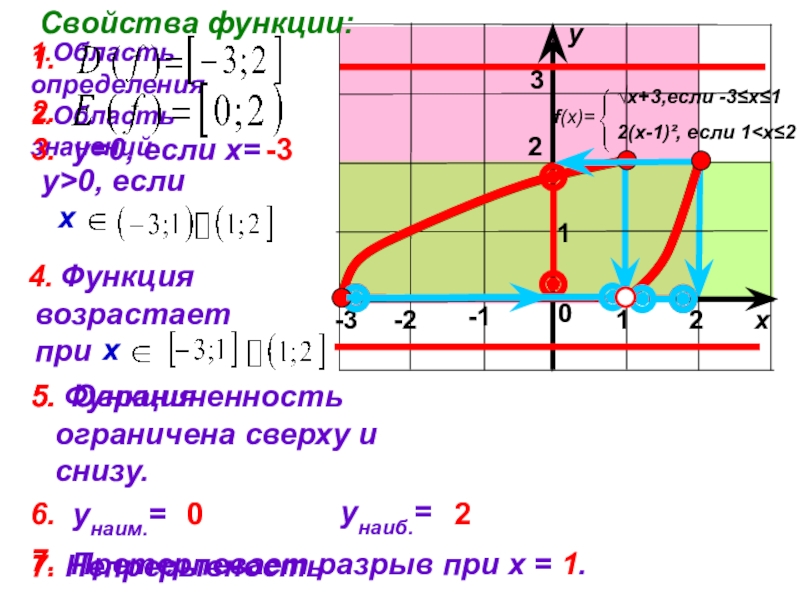
Свойства функции:
1.Область определения
3
-1
2
2.Область значений
3. у=0, если х=
-3
у>0, если
4.
5. Ограниченность
1.
2.
5.
6. унаим.=
унаиб.=
0
2
7. Непрерывность
7.
Претерпевает разрыв при х = 1.
1 2
-3
-2
