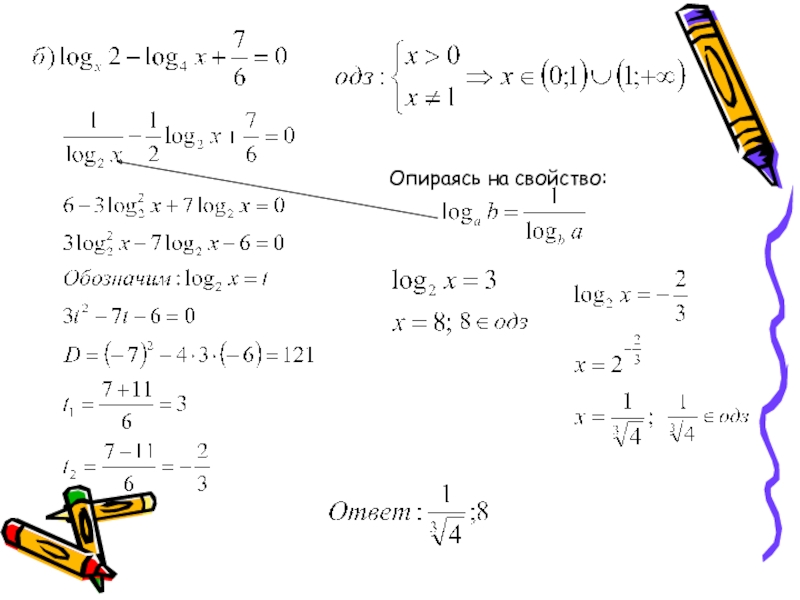- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры в 10 классе Логарифмы. Решение логарифмических уравнений
Содержание
- 1. Презентация к уроку алгебры в 10 классе Логарифмы. Решение логарифмических уравнений
- 2. 1. Логарифмом
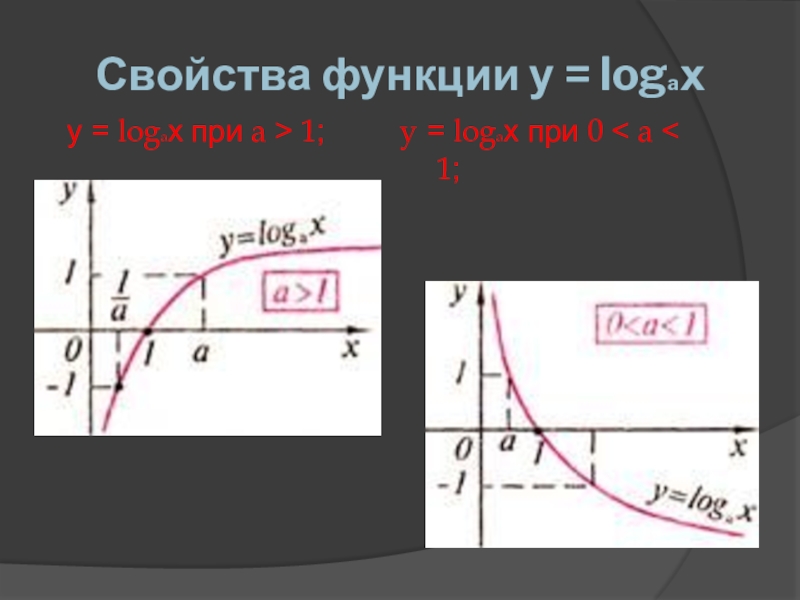
- 3. Свойства функции у = logaху = logaх
- 4. Рассмотрим некоторые свойства логарифма
- 5. Установите соответствие
- 6. Найдите ошибки, поясните
- 7. Вычислите
- 8. Слайд 8
- 9. Выбрать правильный ответ1. Найти область определения:
- 10. Выбрать правильный ответ3. Решите уравнение:log (2+1) =
- 11. Выбрать правильный ответ5. Какое число лишнее?
- 12. Правильные ответы:№ задания
- 13. да "+" нет "-"Графический диктант
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Критерии оценок:За 9-10 правильных ответов – оценка
- 25. Методы решения уравнений:графический метод ;по определению логарифма;потенцирование;замена переменных;логарифмирование
- 26. Слайд 26
- 27. Графический методРешите уравнение
- 28. По определению логарифма:loga x=вx=a , где а≠1 и а>0в
- 29. Пример:logx16=2x =16х≠1 х>0х1 = 4х2 = - 4 – не удовлетворяет условию х>0Ответ: 42
- 30. Потенцированиеloga f(x) = loga g(x)f(x) = g(x),f(x) > 0,g(x) > 0
- 31. Пример:logx (x-1) = logx (2x-8)X-1 = 2x-8,
- 32. Замена переменных:loga f(x) + loga f(x) +
- 33. Пример:2*log0,3 – 7*log0,3 -4 = 0log0,3 x
- 34. Логарифмирование:f(x) = g(x)f(x)>0,g(x)>0loga f(x) = loga g(x)
- 35. Пример: x =
- 36. Решите уравнение
- 37. Опираясь на свойство:
- 38. Подготовка к ЕГЭ Найти наибольший корень уравнения:Ответ: 8Ответ: 7Ответ: 5
- 39. Логарифмы. Применение логарифмов.
- 40. Логарифмы в жизни
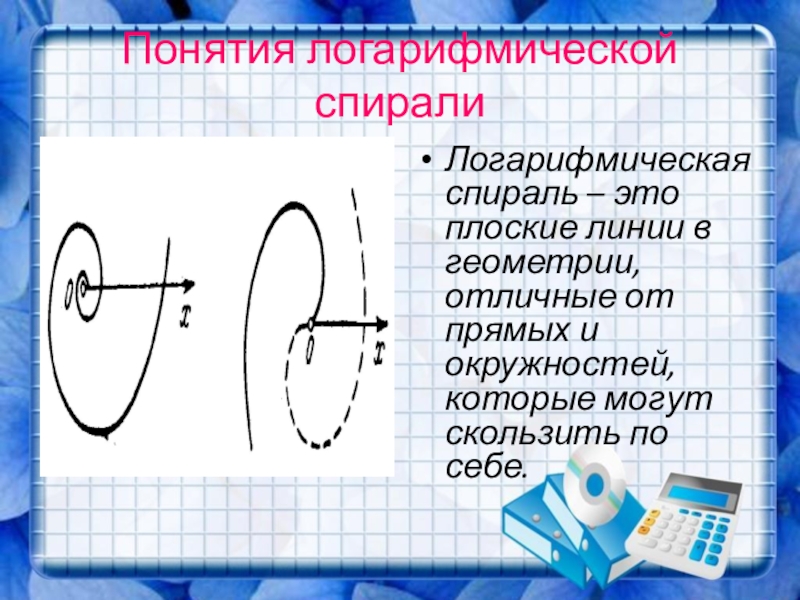
- 41. Понятия логарифмической спирали Логарифмическая спираль – это
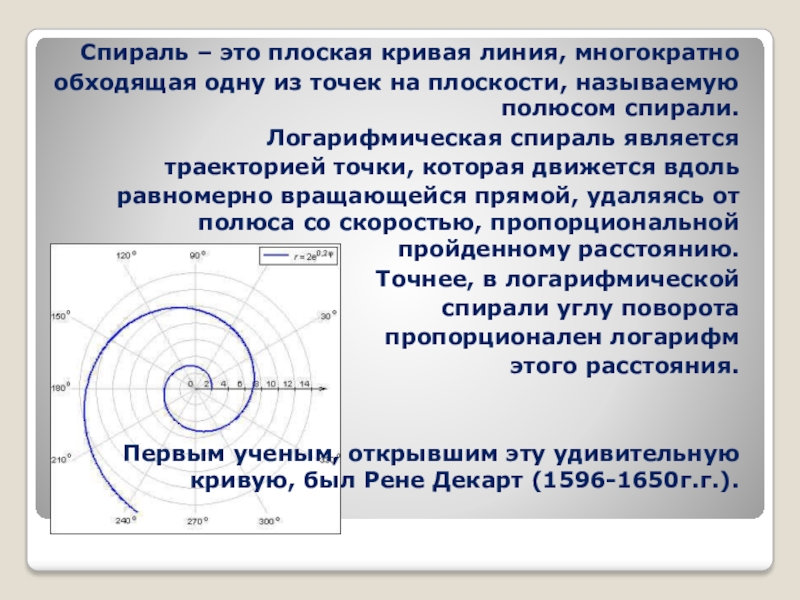
- 42. Спираль – это плоская кривая линия, многократно
- 43. Поэтому раковины многих моллюсков, улиток, а так
- 44. Раковины морских животных могут
- 45. Логарифмическая спираль в природеОдин из наиболее распространенных
- 46. Молекула ДНКЕё молекулы имеют огромную по молекулярным
- 47. Звезды, шум и логарифмыЗаголовок этот, связывающий столь,
- 48. Звезды, шум и логарифмы Шум и
1. Логарифмом числа b по …………… а называется …………….. степени, в которую нужно……………. основание а, чтобы получить число
Слайд 2 1. Логарифмом числа b
по …………… а
называется …………….. степени, в которую
нужно……………. основание а, чтобы
получить число b.
2. Основание и число, стоящее под знаком
логарифма, должны быть………….
3. Если основание а =….., то такой логарифм
называется десятичным и обозначается lg b.
называется …………….. степени, в которую
нужно……………. основание а, чтобы
получить число b.
2. Основание и число, стоящее под знаком
логарифма, должны быть………….
3. Если основание а =….., то такой логарифм
называется десятичным и обозначается lg b.
основанию
показатель
возвести
положительными
10
Продолжи предложение.....
Слайд 9Выбрать правильный ответ
1. Найти область определения:
у = log 1/3
(3x+4)
--------------------------------
2. Решите уравнение:
х = log 27 1/3
--------------------------------
2. Решите уравнение:
х = log 27 1/3
1. (4/3; + ∞),
2. (-4/3; + ∞),
3. (- ∞; -4/3),
4. (- ∞; 4/3)
-----------------------------
1. нет решений
2. х=9
3. х=3
4. х=-1/3
Слайд 10Выбрать правильный ответ
3. Решите уравнение:
log (2+1) = lg х
---------------------
4.Решите уравнение:
lg
х2 = 0
1. х= 1
2. нет решений
3. х= -1
4. х= 0
-------------------------
1. х= +1
2. х= -1
3. х= 1
4. нет решений
Слайд 11Выбрать правильный ответ
5. Какое число лишнее?
1. log3 0,7
2. log1/3 12
3. log 0,5 2/3
4. log 0,3 27
2. log1/3 12
3. log 0,5 2/3
4. log 0,3 27
Слайд 24Критерии оценок:
За 9-10 правильных ответов – оценка «5»
За 7-8 правильных ответов – оценка «4»
За 5-6 правильных ответов – оценка «3» Менее 5 правильных ответов – оценка «2»
За 5-6 правильных ответов – оценка «3» Менее 5 правильных ответов – оценка «2»
Слайд 25Методы решения уравнений:
графический метод ;
по определению логарифма;
потенцирование;
замена переменных;
логарифмирование
Слайд 27Графический метод
Решите уравнение
Log5 x=0
Решение:
Уравнение log5 x=0 имеет один корень x=1,поскольку график функции y=log5 x
пересекает ось х в единственной точке (1;0).
Решение:
Уравнение log5 x=0 имеет один корень x=1,поскольку график функции y=log5 x
пересекает ось х в единственной точке (1;0).
Слайд 31Пример:
logx (x-1) = logx (2x-8)
X-1 = 2x-8,
x=7,
X-1>0, x>1,
2x-8>0, x>4,
x≠1, x≠1,
x>0 x>0
x=7 удовлетворяет всем условиям системы
Ответ: 7
X-1>0, x>1,
2x-8>0, x>4,
x≠1, x≠1,
x>0 x>0
x=7 удовлетворяет всем условиям системы
Ответ: 7
Слайд 32Замена переменных:
loga f(x) + loga f(x) + c=0,
loga f(x) = t,
f(x)>0
t + t + c = 0
Далее решаем квадратное уравнение
Д = t - 4*a*c
Находим t1 и t2
Подставляем значения t1 и t2:
t + t + c = 0
Далее решаем квадратное уравнение
Д = t - 4*a*c
Находим t1 и t2
Подставляем значения t1 и t2:
2
2
loga f(x)=t1
loga f(x)=t2
Слайд 33Пример:
2*log0,3 – 7*log0,3 -4 = 0
log0,3 x = t, x>0
2t -
7t - 4 = 0,
Д = 49 + 32 = 81,
t1 = (7+9) / 4 = 4,
t2 = (7-9) / 4 = -1/2
log0,3 x = 4, log0,3 x = -1/2,
x1 = 0,0081 x2 = √30 / 3
Ответ: 0,0081; √30 / 3
Д = 49 + 32 = 81,
t1 = (7+9) / 4 = 4,
t2 = (7-9) / 4 = -1/2
log0,3 x = 4, log0,3 x = -1/2,
x1 = 0,0081 x2 = √30 / 3
Ответ: 0,0081; √30 / 3
2
2
Слайд 35Пример:
x = 0,04
Прологарифмируем обе
части по основанию 5.
log5x = log50,04
Учтем, что log5x = r*log5x и что log50,04 = -2, следовательно уравнение можно привести к следующему виду:
(1-log5x) * log5x = -2
log5x = y
(1-y) * y = -2
y² - y – 2 = 0,
log5x = 2, log5x = -1
x = 25 x = 1/5
Ответ: 1/5; 25
log5x = log50,04
Учтем, что log5x = r*log5x и что log50,04 = -2, следовательно уравнение можно привести к следующему виду:
(1-log5x) * log5x = -2
log5x = y
(1-y) * y = -2
y² - y – 2 = 0,
log5x = 2, log5x = -1
x = 25 x = 1/5
Ответ: 1/5; 25
1- log5x
1- log5x
r
Слайд 41Понятия логарифмической спирали
Логарифмическая спираль – это плоские линии в геометрии,
отличные от прямых и окружностей, которые могут скользить по себе.
Слайд 42Спираль – это плоская кривая линия, многократно
обходящая одну из точек
на плоскости, называемую полюсом спирали.
Логарифмическая спираль является
траекторией точки, которая движется вдоль
равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию.
Точнее, в логарифмической
спирали углу поворота
пропорционален логарифм
этого расстояния.
Первым ученым, открывшим эту удивительную кривую, был Рене Декарт (1596-1650г.г.).
Логарифмическая спираль является
траекторией точки, которая движется вдоль
равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию.
Точнее, в логарифмической
спирали углу поворота
пропорционален логарифм
этого расстояния.
Первым ученым, открывшим эту удивительную кривую, был Рене Декарт (1596-1650г.г.).
Слайд 43Поэтому раковины многих моллюсков, улиток, а так же рога таких млекопитающих
как архары (горные козлы), закручены по логарифмической спирали.
Семечки в подсолнухе
расположены
по дугам, так же близким к
логарифмической спирали.
Слайд 44 Раковины морских животных могут расти лишь в одном
направлении. Чтобы не слишком вытягиваться им приходиться скручиваться, причём каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали, можно сказать что эта спираль является математическим символом соотношения форм роста.
Слайд 45Логарифмическая спираль в природе
Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину,
закручивает нити вокруг центра по логарифмической спирали.
По логарифмическим спиралям закручены и многие галактики, в частности, галактика которой принадлежит Солнечная Система.
Слайд 46Молекула ДНК
Её молекулы имеют огромную по молекулярным масштабам длину и состоят
из 2-х нитей, сплетённых между собой в двойную спираль. Каждую из нитей можно сравнить с длинной нитки бус. С нитями бус мы сравниваем и белки.
Слайд 47Звезды, шум и логарифмы
Заголовок этот, связывающий столь, казалось бы, несоединимые вещи,
не притязает быть пародией на произведения Кузьмы Пруткова; речь в самом деле пойдет о звездах и о шуме в тесной связи с логарифмами.
Слайд 48Звезды, шум и логарифмы
Шум и звезды объединяются здесь потому,
что и громкость шума и яркость звезд оцениваются одинаковым образом - по логарифмической шкале.
