- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку 8 класса Построение квадратичной функции
Содержание
- 1. Презентация к уроку 8 класса Построение квадратичной функции
- 2. Итак, начнём…
- 3. Отгадав ребус, вы узнаете тему нашего урока
- 4. Квадратичная функция
- 5. Цели урока: 1. Повторить свойства функции.
- 6. Заполни пропуски …1. Функция у =
- 7. Подумай… 1. Найдите координаты вершины параболы у=х2-4х+4Ответ:
- 8. По графику функции у=х2 - 5х +
- 9. 1. Постройте графики функцийy=2x2+8x-10y=-3x2 +6x-3
- 10. Алгоритм построения графика функции у=ах2+bх+c Составить таблицу
- 11. ТестАлгебра щедра. Зачастую она дает больше, чем
- 12. Немного историиМатематики Древней Греции открыли параболу ещё
- 13. Параболы в физическом пространстве Параболическая орбита и движение спутника по нейПадение баскетбольного мячаПараболические траектории струй воды
- 14. Вторая космическая скорость, наименьшая скорость (начальная), которую
- 15. Полезные сайтыhttp://ru.wikipedia.orghttphttp://http://elvirahttp://elvira1215.http://elvira1215.ucozhttp://elvira1215.ucoz.http://elvira1215.ucoz.ruhttp://elvira1215.ucoz.ru/http://elvira1215.ucoz.ru/indexhttp://elvira1215.ucoz.ru/index/2_http://elvira1215.ucoz.ru/index/2_chetverthttp://elvira1215.ucoz.ru/index/2_chetvert_2011_2012/0-22
Слайд 1автор: Потехина Ольга Михайловна
МБОУ Ивановская СОШ
учитель математики,
первая квалификационная категория.
Слайд 5Цели урока:
1. Повторить свойства функции.
2. Решать задачи, используя свойства функции.
3. Применить
Слайд 6 Заполни пропуски …
1. Функция у = aх2 + bx +
2. График функции у = ах2 +b+c при любом а ≠ 0 называют … .
3. Функция у = х2 является … (возрастающей, убывающей) на промежутке х ≤ 0.
4. Область определения функции у = aх2 + bx + c (а ≠ 0) …….
5. Точку пересечения параболы с осью симметрии называют … параболы.
6. При а >0 ветви параболы у = ах2 направлены … .
Если а< о и х ≠ 0, то функция у = ах2 принимает …
(положительные, отрицательные) значения.
квадратичной
параболой
убывающей
вершиной параболы
вверх
отрицательные
R
Слайд 7Подумай…
1. Найдите координаты вершины параболы у=х2-4х+4
Ответ: (2;0)
Найдите для графика
Ответ: (-2; 0), (1; 0)
Не производя построение графика, определите, наибольшее или наименьшее значение
принимает квадратичная функция y=2-5х-3х2
Ответ: наибольшее
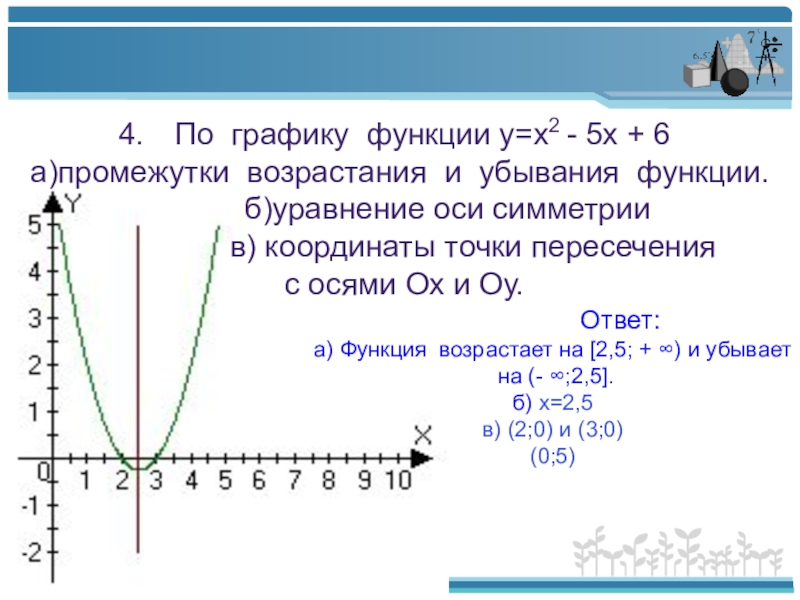
Слайд 8По графику функции у=х2 - 5х + 6
а)промежутки возрастания и
б)уравнение оси симметрии
в) координаты точки пересечения
с осями Ох и Оу.
Ответ:
а) Функция возрастает на [2,5; + ∞) и убывает
на (- ∞;2,5].
б) х=2,5
в) (2;0) и (3;0)
(0;5)
Слайд 91. Постройте графики функций
y=2x2+8x-10
y=-3x2 +6x-3
2. По графикам
промежутки возрастания и убывания функции.
уравнение оси симметрии
координаты точки пересечения с осями Ох и Оу.
Используя программу
Microsoft Excel
Слайд 10Алгоритм построения графика функции у=ах2+bх+c
Составить таблицу значений зависимости переменной У от
впишем в ячейку А1 - х
впишем в ячейку А2 - у=aх2+bх+c
впишем в ячейку В1 начальное значение х
впишем в ячейку С1 следующее значение х и т.д.
выделим содержимое ячеек В1 и С1..., затем с помощью маркера автозаполнения получим соответстветствующие значения х.
впишем в ячейку В2 формулу - =a*В1^2+b*x+c.
скопируем формулу из ячейки В2 методом автозаполнения до последней ячейки.
2. Построение графика.
Выделить подготовленные данные, начиная с заголовка (А1:Н2)
вызовем Мастер диаграмм и выберем вид диаграммы - точечная, тип - со сглаженными линиями без маркеров
Укажем заголовок - (график у=х2+2х-3) и оси - (х,у)
помещаем диаграмму на имеющемся листе – готово
Слайд 11Тест
Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.”
Спасибо за урок
Слайд 12Немного истории
Математики Древней Греции открыли параболу ещё в 260-170 г.г. До
Слайд 13Параболы в физическом пространстве
Параболическая орбита и движение спутника по ней
Падение баскетбольного
Параболические траектории струй воды
Слайд 14Вторая космическая скорость, наименьшая скорость (начальная), которую нужно сообщить телу у