Слайд 1ВГТУ
Всероссийский Конкурс исследовательских проектов, выполненных школьниками и студентами при научном консультировании
ученых
Международной ассоциации строительных вузов
Функция в математике и в жизни.
Выполнил
ученик 8 «Б» класса
МКОУ Калачеевская СОШ №6
КаталандзеРуслан Звиадович
Руководитель
учитель математики
МКОУ Калачеевская СОШ №6
Кашкина Антонина Владимировна
Научный консультант
кандидат физико-математических наук ,
доцент кафедры высшей математики
Воронежского ГТУ
Глазкова Мария Юрьевна
Слайд 2Оглавление
I. Введение
II. Основная часть
III. Заключение
IV. Библиографический список
Слайд 3Введение
Актуальность темы: Реальные процессы в жизни обычно связаны с большим количеством переменных
и зависимостей между ними. Описать эти зависимости можно с помощью функций. Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими. Поэтому изучение функций является актуальным всегда .
Основополагающий вопрос:
каковы области применения математических функций?
какую роль играют математические функции в точных и естественных науках?
что связывает математические функции с историей и филологией?
И возможно ли: Построить график пословицы?
Чем интересны функции?
Цель работы:
Выявить и изучить области, в которых применяется функция и её свойства.
С помощью различных источников информации: толковых словарей, учебной, научно-популярной, художественной литературы осмыслить роль понятия функция как инструмента познания мира и определить его место в картине мира Выявить и изучить области, в которых применяется функция и её свойства.
Слайд 4Задачи:
Пользуясь словарями, найти различные значения термина понятия функция, проанализировать их
с точки зрения математического определения понятия.
Познакомиться с историей формирования понятия функция в математике, проследить тенденции его развития.
Описать особенности применения понятия функция в различных науках и сферах человеческой деятельности.
Подобрать пословицы и поговорки, в которых можно увидеть определение и свойства функции .
Методы проведенных исследований:
Находить нужную литературу, обрабатывать информацию, выполнять и оформлять научно-исследовательскую работу с применением проектной технологии.
Основной метод, который использовался в работе, - это метод систематизации и обработки данных.
Слайд 5Гипотеза: функциональные зависимости существуют во всех сферах жизни человека
Основные результаты исследования:
Применение
темы « Функция» в практической деятельности человека. Презентация для выступления на научно-практической конференции школьников
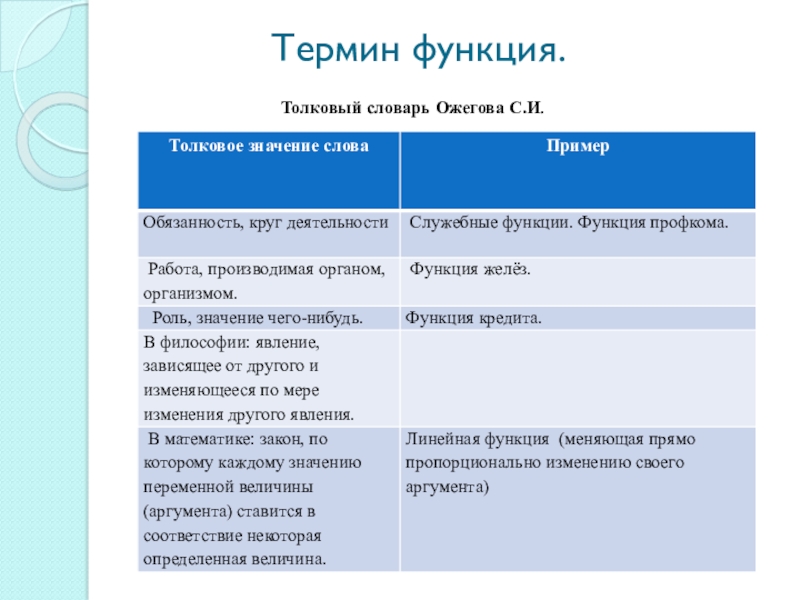
Слайд 6Термин функция.
Толковый словарь Ожегова С.И.
Слайд 7Значимость понятия функция
Функция – это одно из основных общенаучных и математических
понятий, выражающее зависимость между переменными величинами.
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Само слово «функция» происходит от латинского functio — исполнение, осуществление
Слайд 9Определение функции в математике
Определение функции можно дать несколькими способами. Все они
будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами. Любой физический закон, любая формула отражает такую взаимосвязь величин.
Знакомое обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины x по определенному закону, или правилу, обозначаемому f.
2. Функция – это определенное действие над переменной.
Это означает, что мы берем величину x, делаем с ней определенное действие (например, возводим в квадрат) – и получаем величину y.
Определение: Числовая функция у = f(x) – с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х. При этом переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной.
Слайд 10Основные характеристики функций
Изучить заданную функцию –это значит охарактеризовать ход ее изменения
(ее поведение) при изменении независимой переменной. Я рассмотрю не все характеристики функции, а только те, которые мне понадобятся в моем практическом исследовании
Возрастающая функция
Функция у = f(x) называется возрастающей на множестве , если для любых х1 и х2 множества Х, таких, что х1 < х2 выполняется неравенство f(x1) < f(x2)
Слайд 11
Убывающая функция
Функция у = f(x) называется убывающей
на множестве Х, если для любых х1 и х2 множества Х, таких, что х1 < х2 выполняется неравенство f(x1) > f(x2)
Слайд 12 Ограниченность функции
Функцию у= f(x) называют ограниченной снизу если все значения
функции больше некоторого числа.
Функцию у = f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа.
Слайд 16В формировании современного понимания функциональной зависимости приняли участие многие крупные математики.
Описание функции, близкое современному определению, встречается уже в учебниках математики начала XIX века. Активным сторонником такого понимания функции был Н.И. Лобачевский.
Почему мы обозначаем функцию символом f, и когда он появился? Этот символ изобрел в 1733 г. французский математик Клеро А появился этот символ, когда формировался общий подход к понятию функции, когда потребовалось обозначение «функции вообще».
Слайд 17Исследуя понятие функция, делаем вывод:
Математические методы изучения функций
являются наиболее общими ,так как математика изучает не каждую ситуацию в отдельности, а сразу все ситуации, которые можно описать одним законом.
Понятие функция – это инструмент, с помощью которого человек познает мир, поэтому оно является одним из основных и важных понятий.
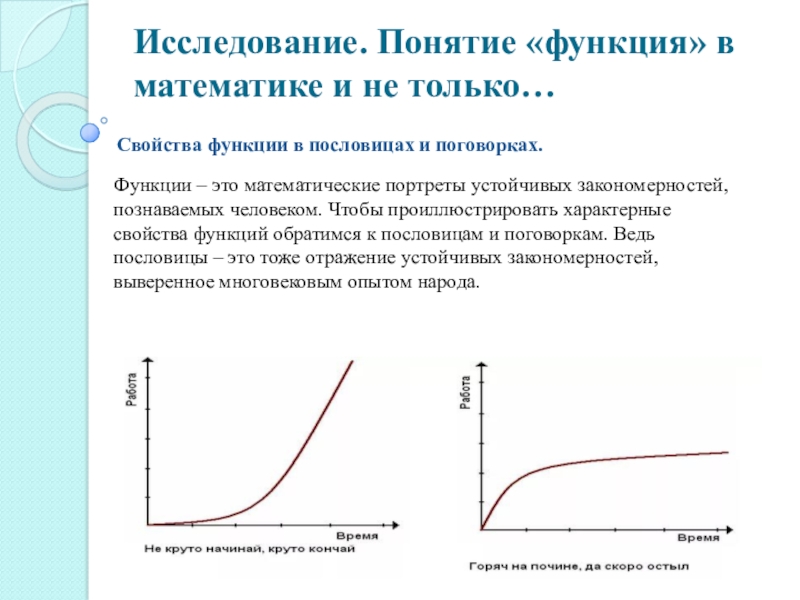
Слайд 18Исследование. Понятие «функция» в математике и не только…
Свойства функции в пословицах
и поговорках.
Функции – это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций обратимся к пословицам и поговоркам. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа.
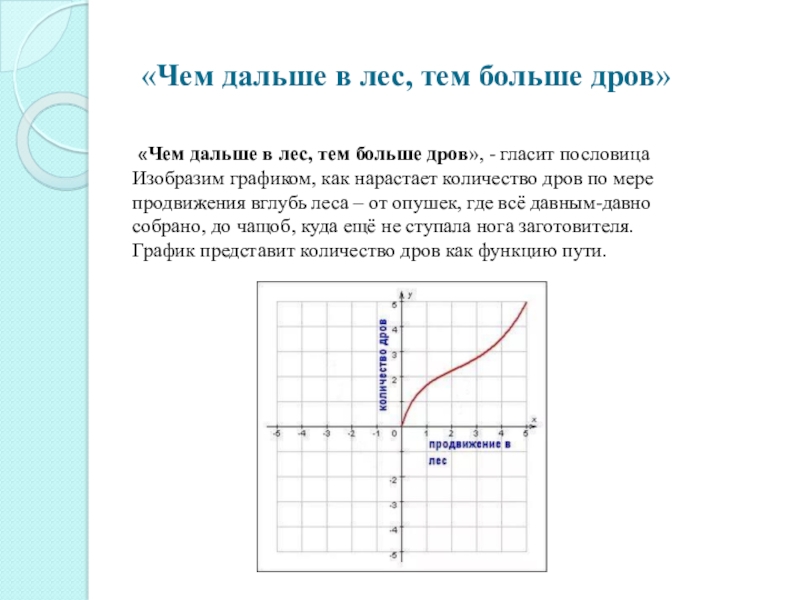
Слайд 19 «Чем дальше в лес, тем больше дров»
«Чем дальше
в лес, тем больше дров», - гласит пословица Изобразим графиком, как нарастает количество дров по мере продвижения вглубь леса – от опушек, где всё давным-давно собрано, до чащоб, куда ещё не ступала нога заготовителя. График представит количество дров как функцию пути.
Слайд 20Убывающая функция.
«Дальше от кумы – меньше греха»
Функция, которая показывает, как
изменяется мера греха по мере удаления от кумы, монотонно убывающая
Мера греха
Расстояние до кумы
Слайд 21Ограниченность функции:« Выше меры конь не скачет».
Если изобразить траекторию скачущего коня,
то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой».
Слайд 22 Максимум функции:«Пересев хуже недосева», - издавна говорили земледельцы.
Вековой опыт свидетельствовал:
урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому, что при чрезмерной густоте ростки начинают глушить друг друга. Эта закономерность станет особенно наглядной, если изобразить её графиком , где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру.
Слайд 24«Функция» в астрономии»
Каждая планета движется в плоскости, проходящей через центр Солнца,
причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Промежутку времени (аргументу) соответствует площадь сектора орбиты.
Слайд 25 Функция в окружающем мире.
Сложная функция, или суперпозиция
Количество топлива, потребляемому заводами
и фабриками планеты, соответствует определённое количество пыли и копоти, выбрасываемое в атмосферу, а этому количеству соответствует определённое количество солнечной энергии, поглощаемое ледниками
Слайд 26Сложная функция, или суперпозиция
Слайд 27Основные математические функции и области их применения в нашей жизни.
Линейная функция:
y=kx+b Графиком линейной функции является прямая. С ней мы встречаемся на уроках физики, химии, а также в повседневной жизни.
Слайд 28Квадратичная функция в окружающем мире
Квадратичная функция является наиболее хорошо изученной
функцией, она довольно часто встречается на практике. Графиком квадратичной функции является парабола. Хорошо известно, что траектория прыжков животных близка к параболе. Замечательное свойство параболы широко используется в науке и технике, например, параболическая арка; свод моста. Известно также, что многие законы природы выражаются в виде квадратичной зависимости.
Слайд 30 Обратная пропорциональность вокруг нас . Закон спроса и предложения.
Слайд 31 Гипербола на защите нашей Родины
Слайд 32 Исследование: «Мой первый в жизни график»
Мама сохранила в альбоме данные
моего роста с рождения по данный момент времени. Это яркий пример табличного задания функции.
График должен быть дискретным, то есть изображаться точками на плоскости, так как функция задана только в определенных точках. Для наглядности я эти точки соединил. Получился график моего роста.
Слайд 34Несерьёзно о серьёзном. Закон глупости.
Если миллион человек верит в какую-то глупость,
она все равно останется глупостью.
Слайд 35Заключение
Вывод: Таким образом, изучив и проанализировав литературу по
истории развития функций, их применения в науке, технике и в окружающем мире, я убедился, что между величинами существует функциональная связь, а также мне удалось показать, что понятие “функция” находит широкое применение в жизни человека. В рамках одной работы невозможно рассмотреть все многообразие окружающих нас функций. Я считаю, что мне удалось показать некоторые примеры нестандартного взгляда на применение математических понятий и функций в окружающей нас жизни.
Моя гипотеза: функциональные зависимости существуют во всех сферах жизни человека подтвердилась.
Функция – это просто, сложно, интересно!
Слайд 36 Библиографический список:
Интернет-ресурсы
http://ru.wikipedia.org – Википедия – свободная энциклопедия
http://www.nigma.ru – интеллектуальная
поисковая система
1. В.И. Даль. Пословицы русского народа. Сборник в двух томах. -М.: худ. Лит.,1989.
2.Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного
чтения 9 – 10 кл. – 2 – е изд., испр. – М.: Просвещение, 1993.
3. Глейзер Г.И. История математики в школе: 9-10 класс - М.:
Просвещение. - 1983.
4. Ульяновская Н. Н. О, функция, как ты важна // Математика. – 1999.
5. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: кн. для учащихся. -М.:Просвещение,1998.
6. Мордкович А.Г. Алгебра. 9 класс. Учебник для учащихся общеобразовательных учреждений. – М: Мнемозина, 2012.
7. Ожегов С.И. Шведова Н.Ю.Толковый словарь русского языка.- М.: Аз; Издание 3-е, стер. 1996.- 928с.
8. Блох А. «Законы Мерфи»/ пер. с англ. Е.Г.Гендель, Минск, «Попурри», 2009.