- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс
Содержание
- 1. Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс
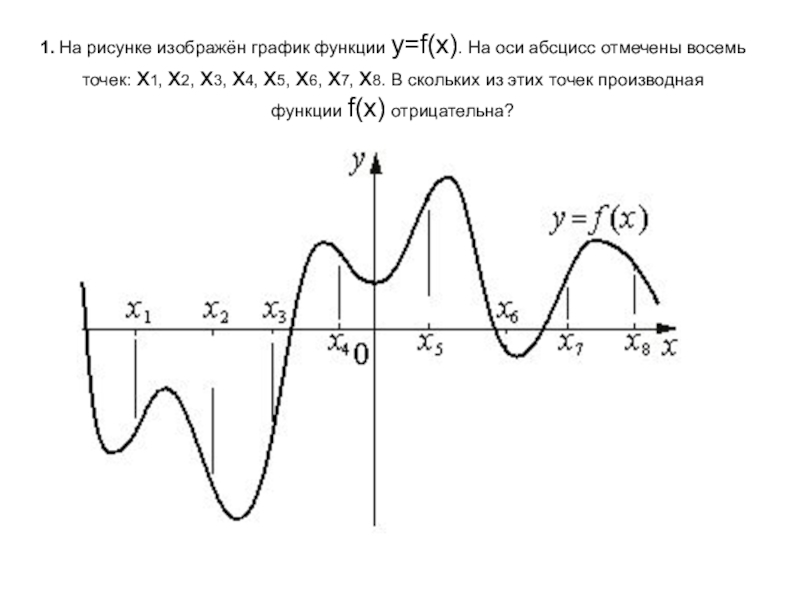
- 2. 1. На рисунке изображён график функции y=f(x). На
- 3. 2. На рисунке изображён график функции y=f(x). На
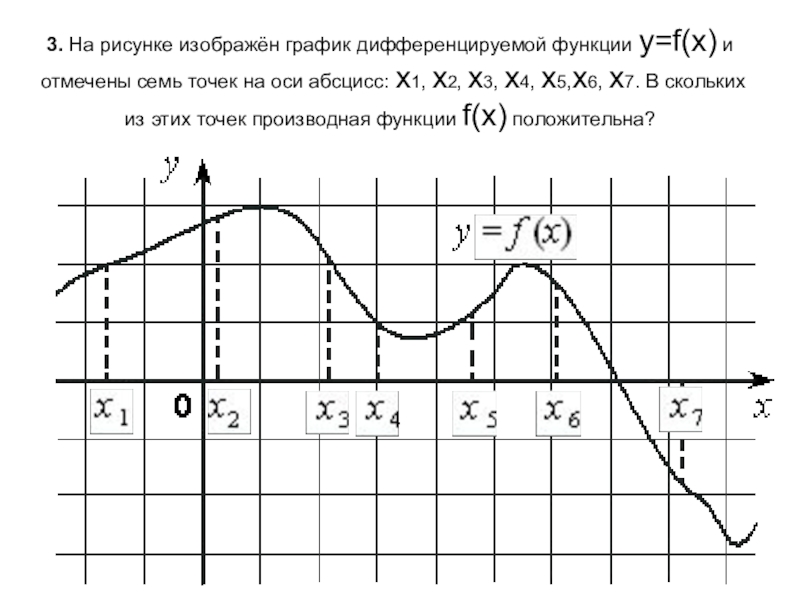
- 4. 3. На рисунке изображён график дифференцируемой функции y=f(x) и
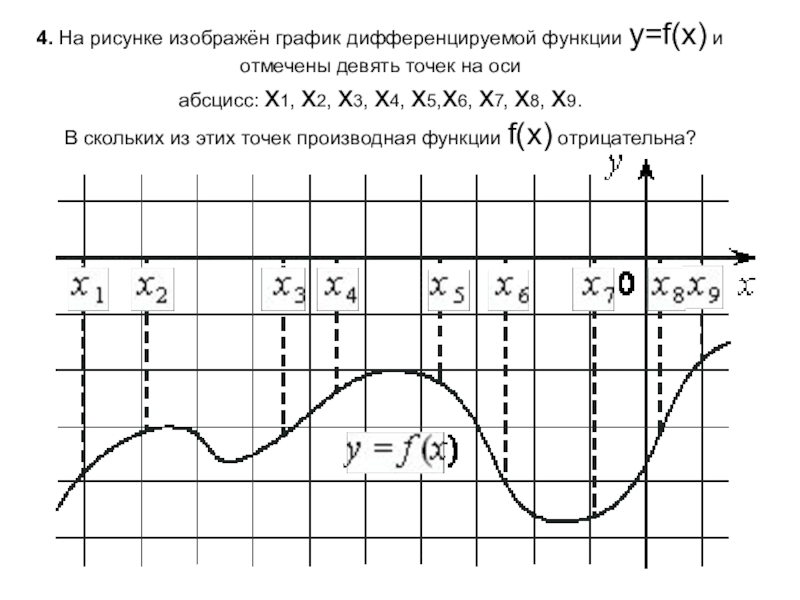
- 5. 4. На рисунке изображён график дифференцируемой функции y=f(x) и
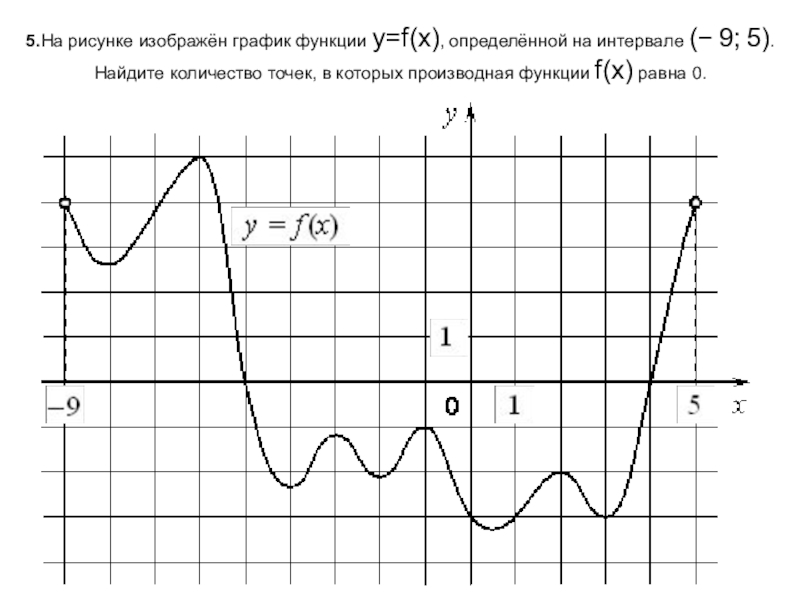
- 6. 5.На рисунке изображён график функции y=f(x), определённой на
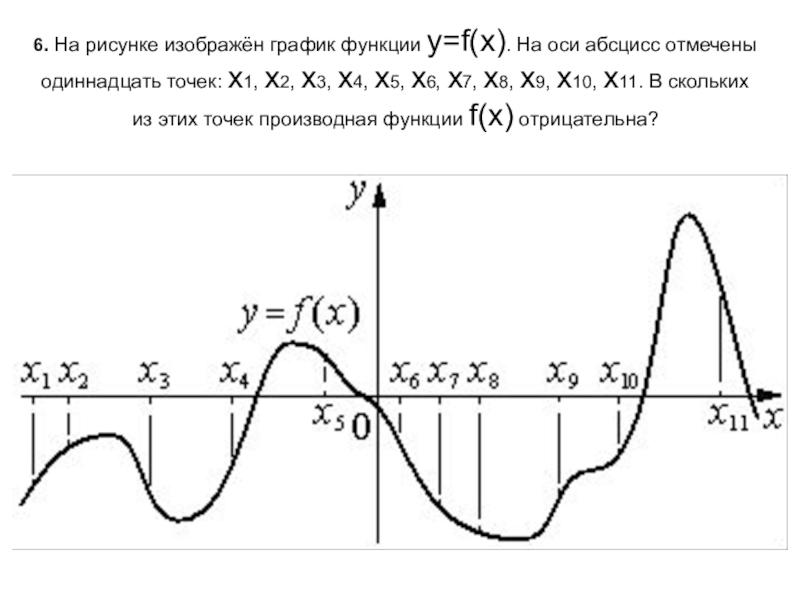
- 7. 6. На рисунке изображён график функции y=f(x). На
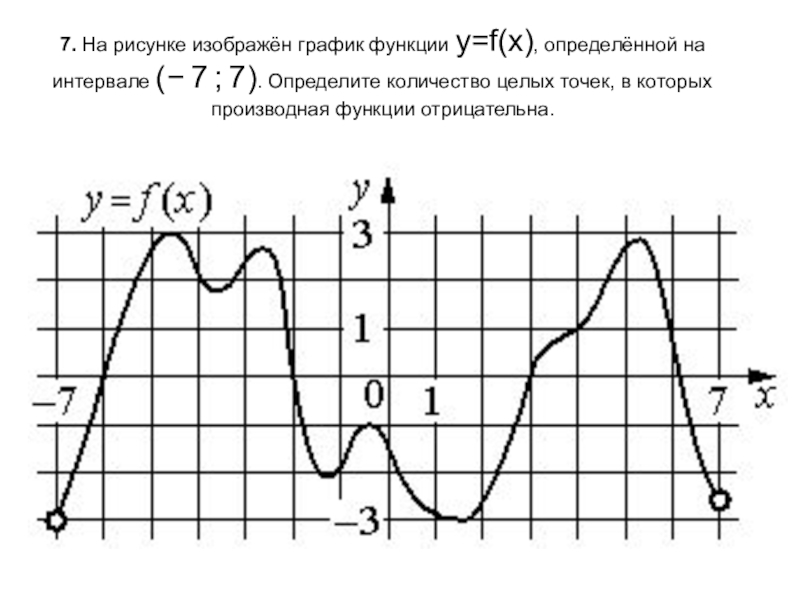
- 8. 7. На рисунке изображён график функции y=f(x), определённой
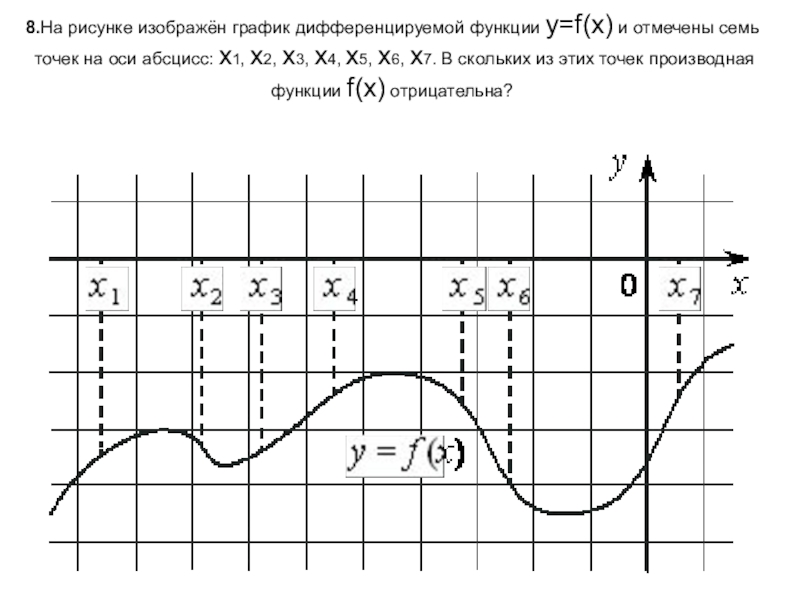
- 9. 8.На рисунке изображён график дифференцируемой функции y=f(x) и отмечены
- 10. 9. На рисунке изображены график дифференцируемой функции y=f(x) и
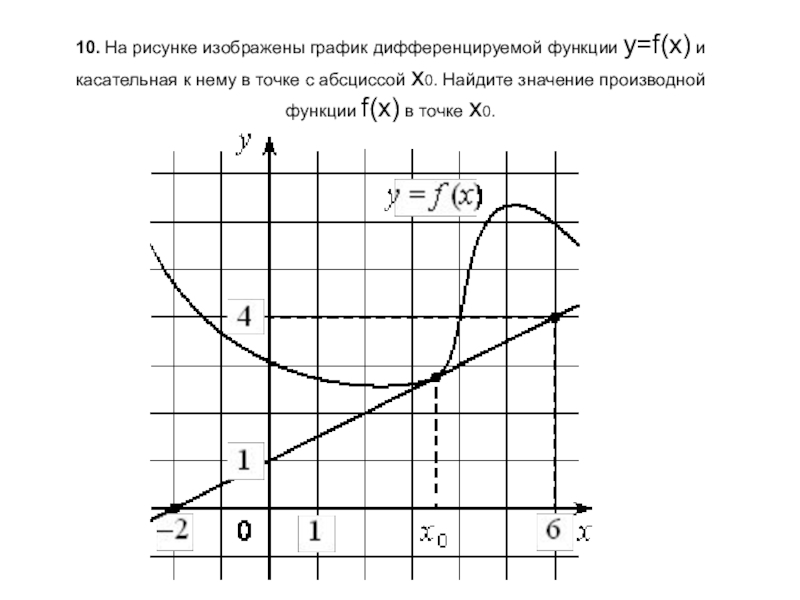
- 11. 10. На рисунке изображены график дифференцируемой функции y=f(x) и
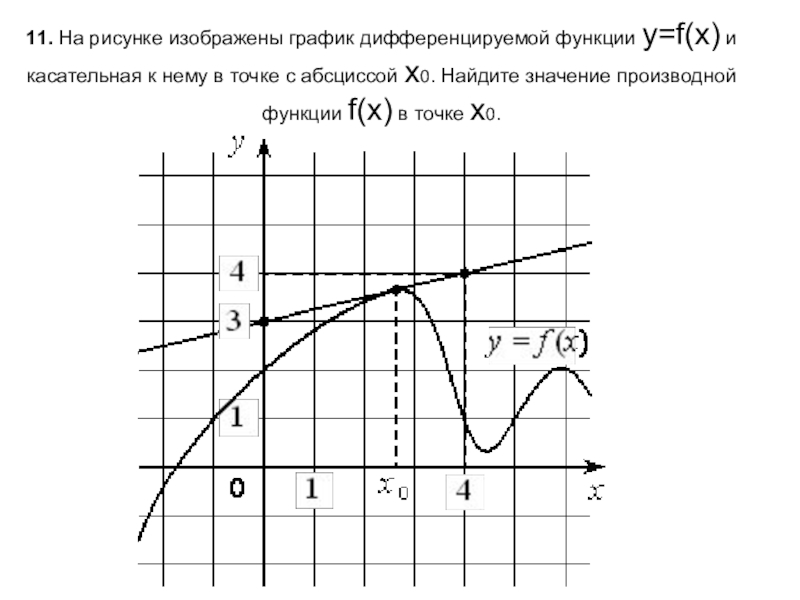
- 12. 11. На рисунке изображены график дифференцируемой функции y=f(x) и
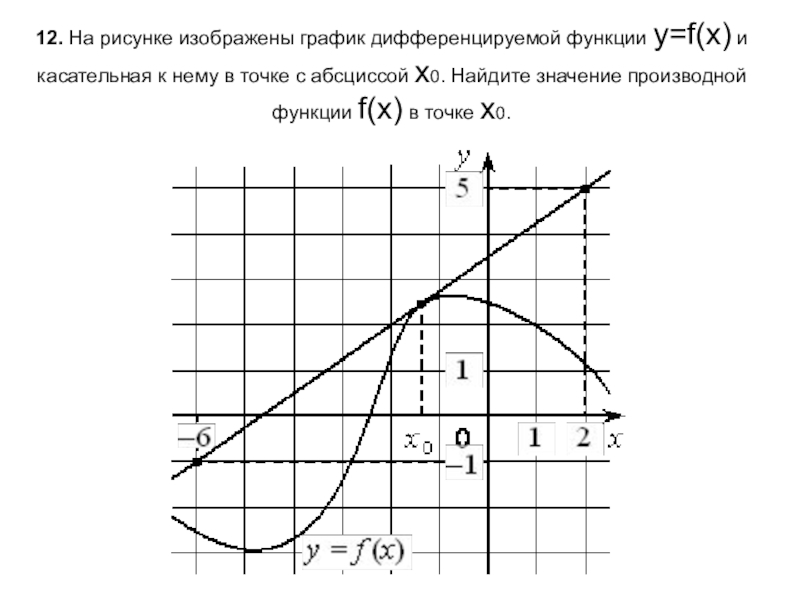
- 13. 12. На рисунке изображены график дифференцируемой функции y=f(x) и
- 14. 13. На рисунке изображены график дифференцируемой функции y=f(x) и
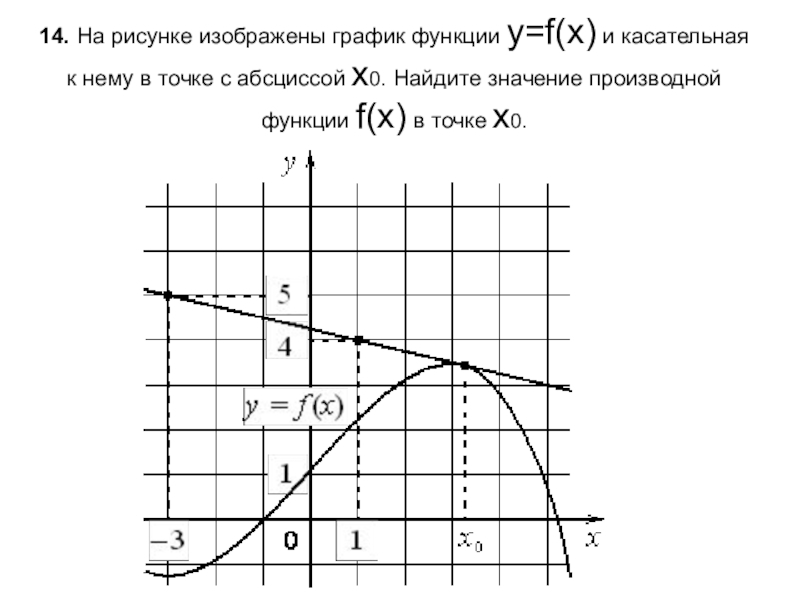
- 15. 14. На рисунке изображены график функции y=f(x) и касательная
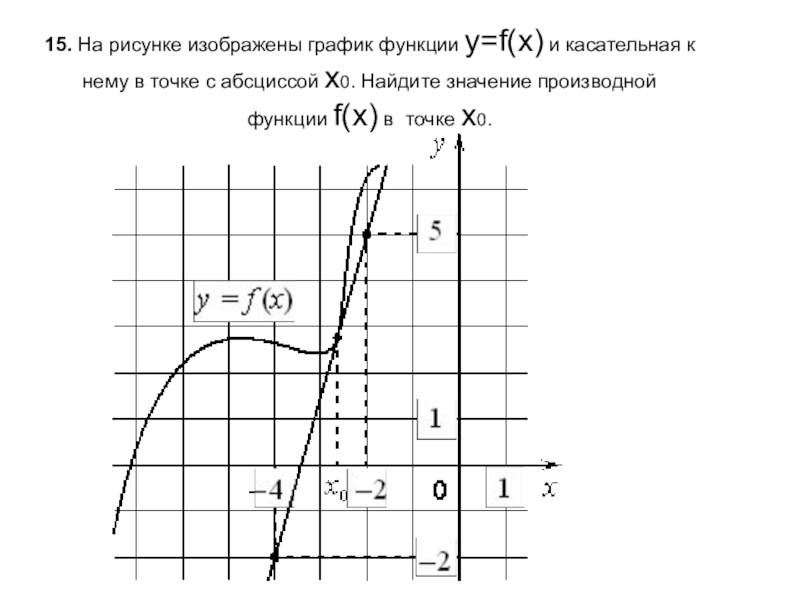
- 16. 15. На рисунке изображены график функции y=f(x) и касательная
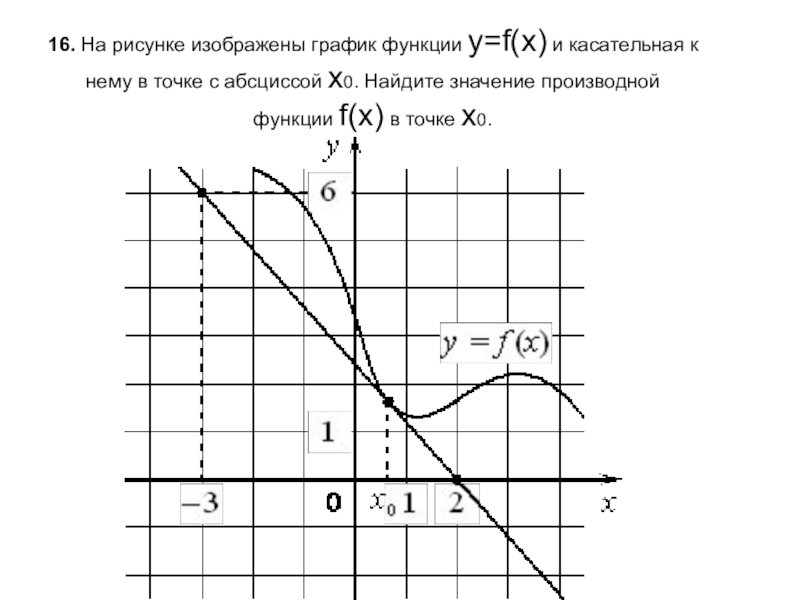
- 17. 16. На рисунке изображены график функции y=f(x) и касательная
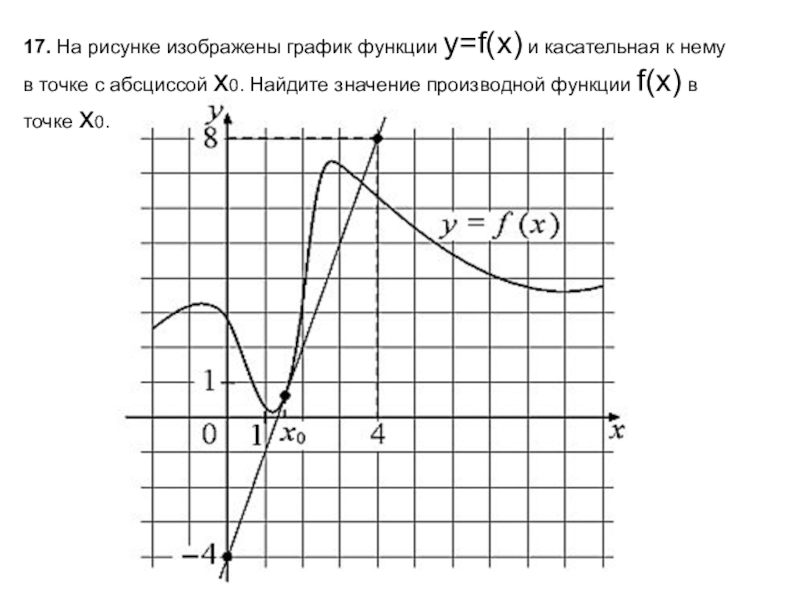
- 18. 17. На рисунке изображены график функции y=f(x) и
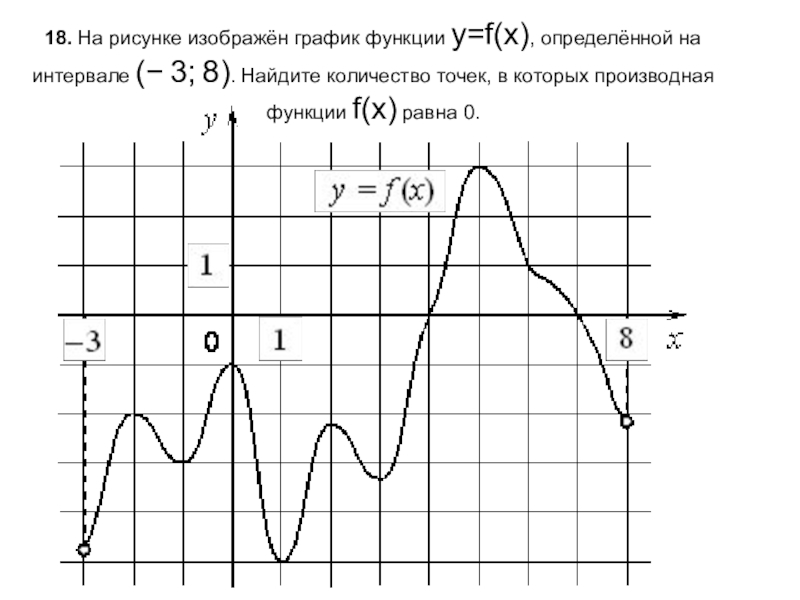
- 19. 18. На рисунке изображён график функции y=f(x), определённой
- 20. 19.На рисунке изображён график дифференцируемой функции y=f(x), определённой
- 21. 20. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
- 22. 21. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 3). В какой точке отрезка [− 6; −1] функция f(x) принимает наименьшее значение?
- 23. 22. На рисунке изображён график y=f '(x) — производной функции f(x). На
- 24. 23. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].
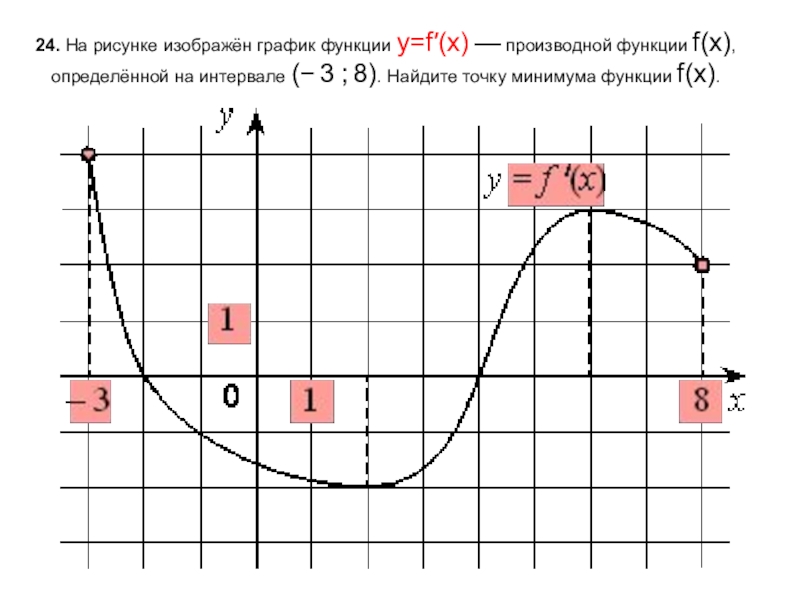
- 25. 24. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите точку минимума функции f(x).
- 26. 25. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?
- 27. 26. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
- 28. 27. На рисунке изображён график y=f '(x) — производной функции f(x), определённой
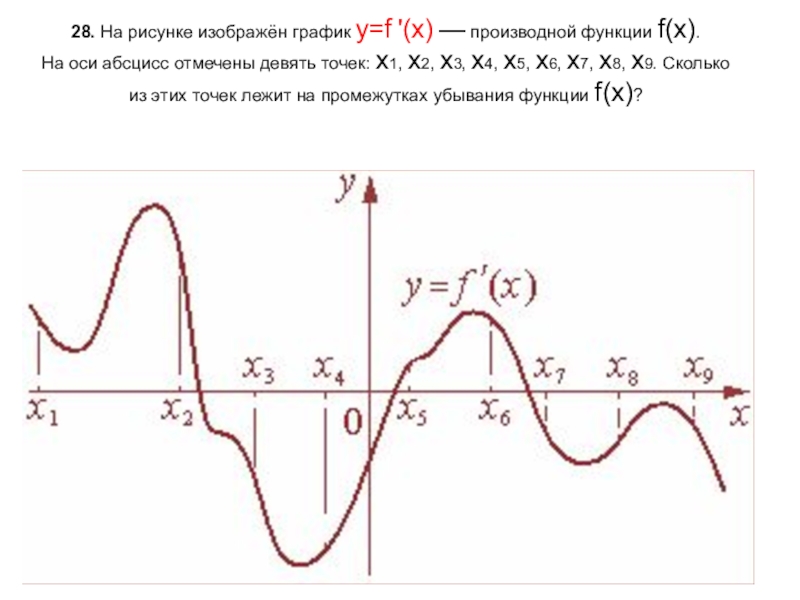
- 29. 28. На рисунке изображён график y=f '(x) — производной функции f(x). На
- 30. 29. На рисунке изображён график y=f '(x) — производной функции f(x), определённой
- 31. 30. На рисунке изображён график функции y=f(x) и отмечены
- 32. 31. На рисунке изображены график функции и
- 33. 32. На рисунке изображён график функции y=f(x).
- 34. 33. На рисунке изображены график функции и
- 35. 1. Найдите наименьшее значение функции y=(x2+9)/x на
Слайд 21. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь
Слайд 32. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены семь
Слайд 43. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на
Слайд 54. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены девять точек на
Слайд 65.На рисунке изображён график функции y=f(x), определённой на интервале (− 9; 5). Найдите количество точек,
Слайд 76. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены одиннадцать
Слайд 87. На рисунке изображён график функции y=f(x), определённой на интервале (− 7 ; 7). Определите количество
Слайд 98.На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси
Слайд 109. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в
Слайд 1110. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в
Слайд 1211. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в
Слайд 1312. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в
Слайд 1413. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в
Слайд 1514. На рисунке изображены график функции y=f(x) и касательная к нему в точке
Слайд 1615. На рисунке изображены график функции y=f(x) и касательная к нему в точке
Слайд 1716. На рисунке изображены график функции y=f(x) и касательная к нему в точке
Слайд 18
17. На рисунке изображены график функции y=f(x) и касательная к нему в
Слайд 1918. На рисунке изображён график функции y=f(x), определённой на интервале (− 3; 8). Найдите количество
Слайд 2019.На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (1 ; 10). Найдите точку
Слайд 2120. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой
Слайд 2221. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 3). В какой
Слайд 2322. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечены шесть точек: x1, x2, x3, x4, x5, x6. Сколько
Слайд 2423. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на
Слайд 2524. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите
Слайд 2625. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой
Слайд 2726. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 4). В какой
Слайд 2827. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество
Слайд 2928. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечены девять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9. Сколько
Слайд 3029. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3 ; 19). Найдите количество
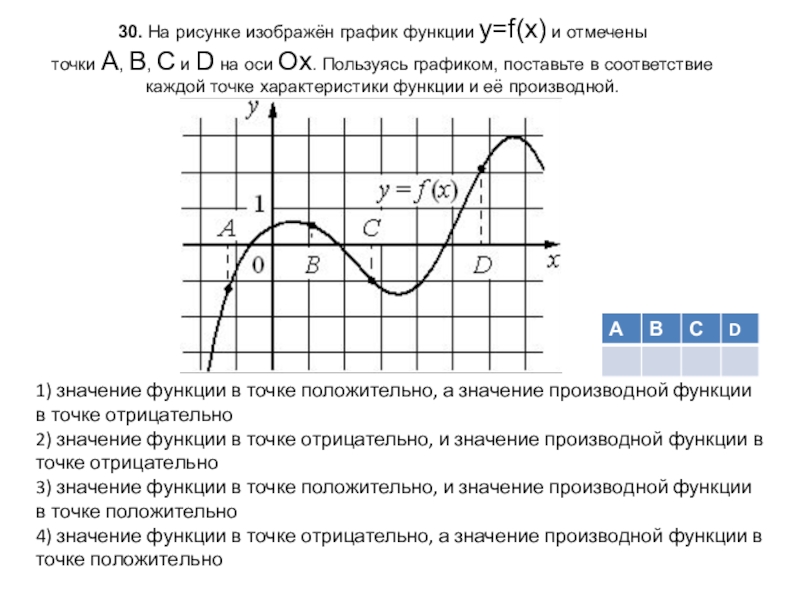
Слайд 3130. На рисунке изображён график функции y=f(x) и отмечены точки A, B, C и D на оси Ox. Пользуясь графиком,
1) значение функции в точке положительно, а значение производной функции в точке отрицательно
2) значение функции в точке отрицательно, и значение производной функции в точке отрицательно
3) значение функции в точке положительно, и значение производной функции в точке положительно
4) значение функции в точке отрицательно, а значение производной функции в точке положительно
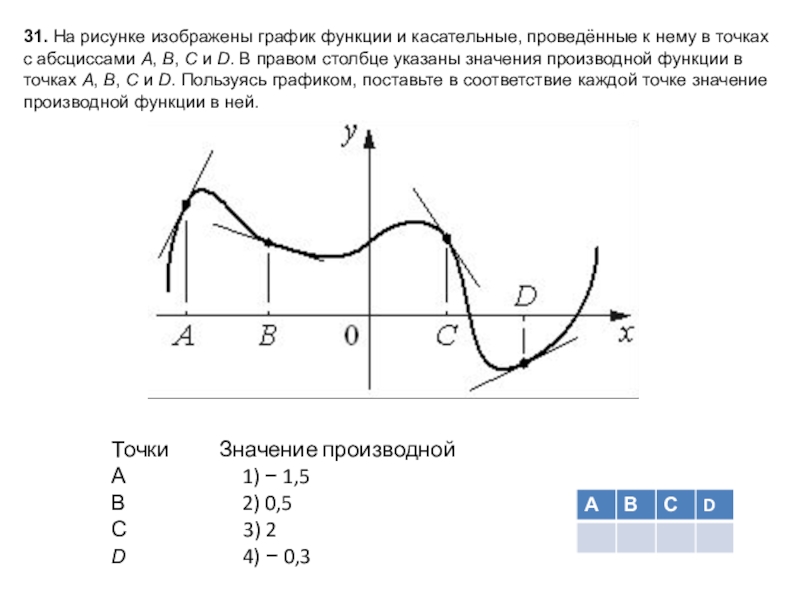
Слайд 3231. На рисунке изображены график функции и касательные, проведённые к нему
Точки Значение производной
А 1) − 1,5
В 2) 0,5
С 3) 2
D 4) − 0,3
Слайд 3332. На рисунке изображён график функции y=f(x). Числа a, b, c,
ИНТЕРВАЛЫ ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ
А) (a; b) 1) значения функции положительны в каждой точке интервала
Б) (b; c) 2) значения функции отрицательны в каждой точке интервала
В) (c; d) 3) значения производной функции отрицательны в каждой точке интервала
Г) (d; e) 4) значения производной функции положительны в каждой точке интервала
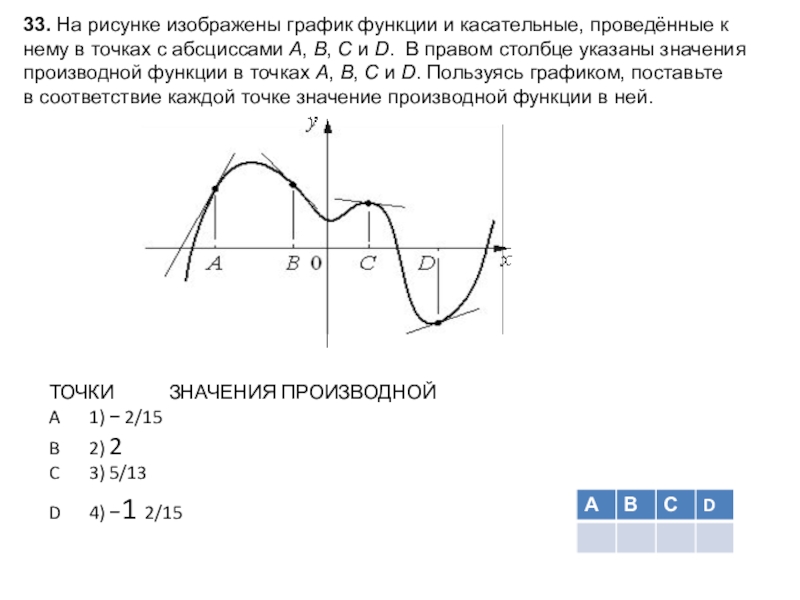
Слайд 3433. На рисунке изображены график функции и касательные, проведённые к нему
ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
A 1) − 2/15
B 2) 2
C 3) 5/13
D 4) −1 2/15
Слайд 351. Найдите наименьшее значение функции y=(x2+9)/x на отрезке [1 ; 11].
2. Найдите наименьшее
3. Найдите наибольшее значение функции y=x3−6x2+9x+5 на отрезке [0; 3].
4. Найдите наименьшее значение функции y=(x−9)2(x+4)−4 на отрезке [7 ; 16].
5. Найдите наибольшее значение функции y=x3−12x+5 на отрезке [− 3 ; 0].
Найдите наименьшее значение функции y=(x2+49)/x на отрезке [1 ; 19].
6. Материальная точка движется прямолинейно по закону x(t)=1/6 t3−2 t2+6 t+250, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 96 м/с?
7. Найдите наибольшее значение функции y=(x−8)2(x−9)−10 на отрезке [2 ; 8,5].
8. Найдите точку максимума функции y=ln(x+2)−5x+13.
9. Найдите точку максимума функции y=ln(x+6)−5x+4.
10. Материальная точка движется прямолинейно по закону x(t)=1/6 t3+t2−8 t+180, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 40 м/с?
11. Найдите наибольшее значение функции y=10⋅ln(x+8)−10x−18 на отрезке [− 7,5 ; 0].
12. Найдите наибольшее значение функции y=59x−56sinx+42 на отрезке [− π/2; 0].




![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 19.На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (1 ; 10). Найдите точку 19.На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (1 ; 10). Найдите точку из отрезка [2 ; 6], в которой производная функции f(x) равна](/img/thumbs/c18d0cdc076d62ca4cb49f754edf12a6-800x.jpg)
![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 20. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение? 20. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?](/img/thumbs/515c33b03b1f558ac34b77e98a2da0a8-800x.jpg)
![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 21. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 3). В какой точке отрезка [− 6; −1] функция f(x) принимает наименьшее значение? 21. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 3). В какой точке отрезка [− 6; −1] функция f(x) принимает наименьшее значение?](/img/thumbs/ff38cf9cb4baf5084cb33e41de631229-800x.jpg)

![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 23. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3]. 23. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].](/img/thumbs/b0236f23321ad0e95ec490dc8ffbf569-800x.jpg)
![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 25. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение? 25. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?](/img/thumbs/d27c76388201f8e90278837356a516dd-800x.jpg)
![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 26. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение? 26. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?](/img/thumbs/e8c1eab68e4028acc76f77aabcbaba37-800x.jpg)
![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 27. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество 27. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6 ; 4].](/img/thumbs/d7e58f96668fbcf96465781001db943a-800x.jpg)
![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 29. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3 ; 19). Найдите количество 29. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3 ; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2 ; 15].](/img/thumbs/5f1dea7ccd22d066de917b705819b908-800x.jpg)

![Презентация для подготовки к ЕГЭ, ГВЭ по математике на тему Производная 11 класс 1. Найдите наименьшее значение функции y=(x2+9)/x на отрезке [1 ; 11].2. Найдите наименьшее 1. Найдите наименьшее значение функции y=(x2+9)/x на отрезке [1 ; 11].2. Найдите наименьшее значение функции y=x3−x2−8x+4 на отрезке [1; 7].3. Найдите наибольшее значение](/img/thumbs/8eb3c02bc9e7d4cc961c1177e5e9f151-800x.jpg)





