- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Алгебраические неравенства для 11 класса
Содержание
- 1. Презентация Алгебраические неравенства для 11 класса
- 2. ЦЕЛЬ УРОКА:обобщение и систематизация знаний по теме «Алгебраические неравенства»;развитие интеллектуальных способностей;воспитание ответственности, самостоятельности.
- 3. Линейные неравенства
- 4. Свойства неравенств:Если из одной части неравенства перенести
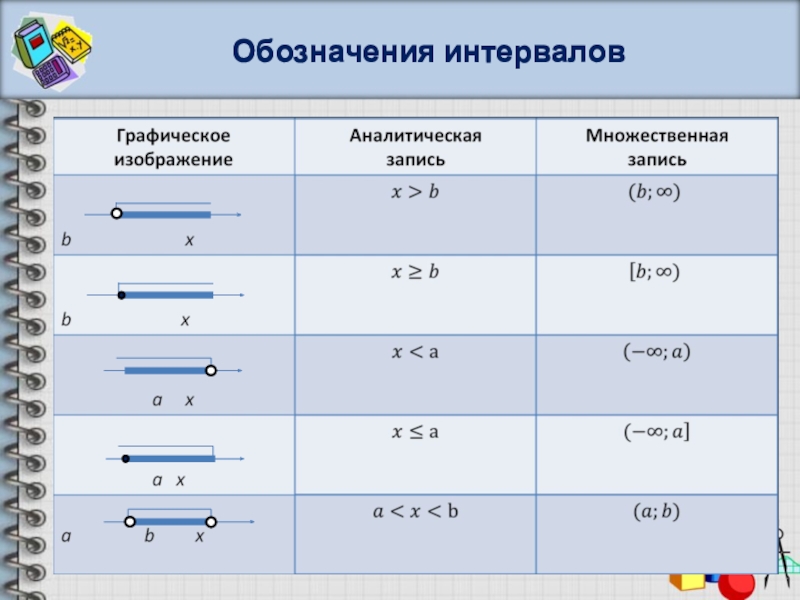
- 5. Обозначения интерваловОбозначения интервалов
- 6. Обозначения интервалов
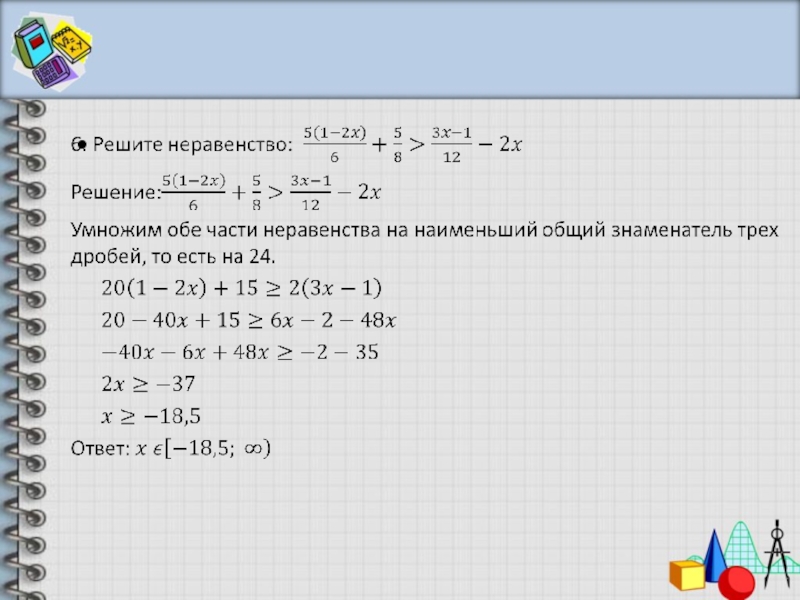
- 7. Примеры решения линейных неравенств
- 8. Примеры решения линейных неравенств
- 9. Примеры решения линейных неравенств
- 10. Примеры решения линейных неравенств
- 11. Примеры решения линейных неравенств
- 12.
- 13. Примеры решения линейных неравенств
- 14. Метод интервалов (промежутков)
- 15. Метод интервалов (промежутков)
- 16. Применение метода интервалов x-2012
- 17. Применение метода интервалов x
- 18. Обобщенный метод интервалов (промежутков) xx
- 19. Обобщенный метод интервалов (промежутков) xx
- 20. Применение обобщенного метода интервалов 7-3x
- 21. Применение обобщенного метода интервалов x1234
- 22. Применение обобщенного метода интервалов -20123x
- 23. Обобщенный метод интервалов (промежутков)
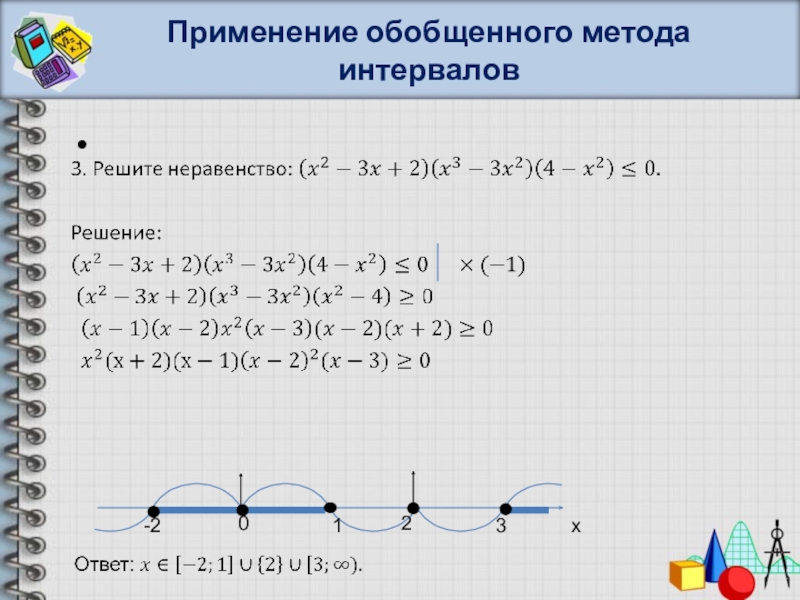
- 24. Применение обобщенного метода интервалов
- 25. Применение обобщенного метода интервалов
- 26. Решение рациональных неравенств
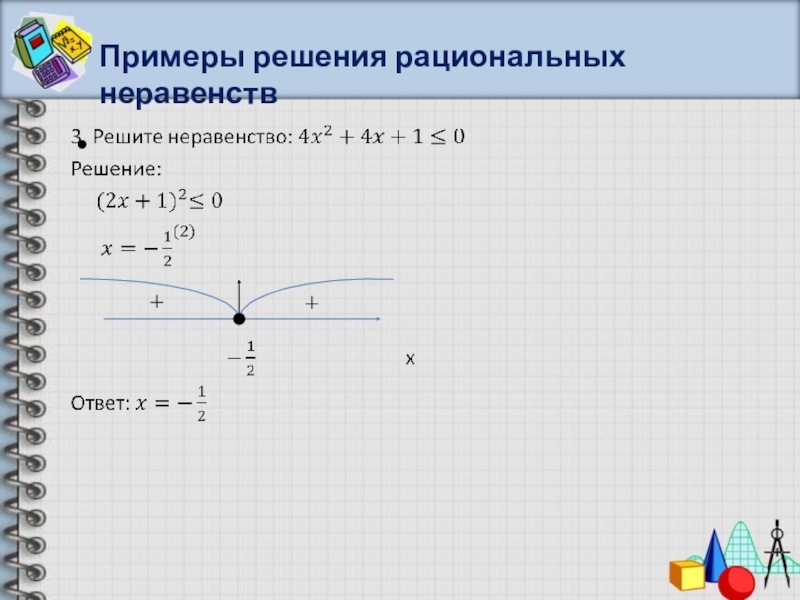
- 27. Примеры решения рациональных неравенств
- 28. Примеры решения рациональных неравенств
- 29. Примеры решения рациональных неравенств
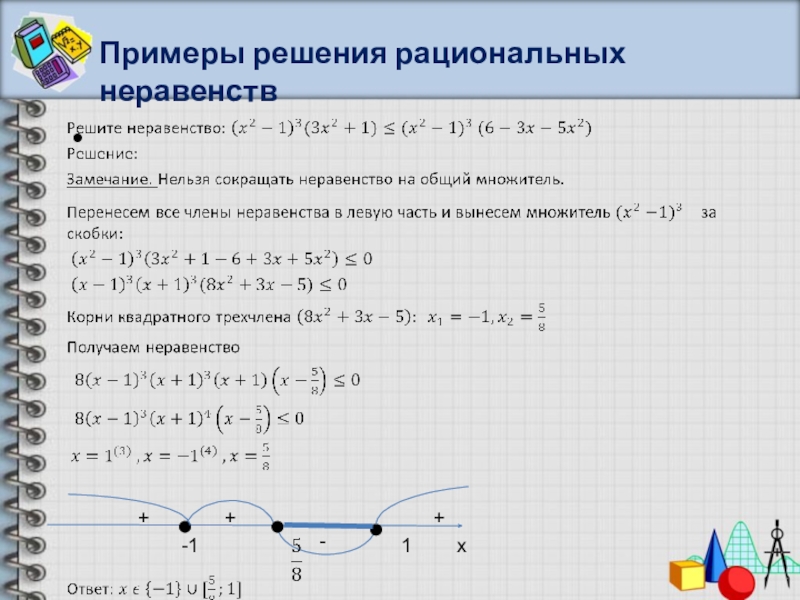
- 30. Примеры решения рациональных неравенств++-+x-1 1
- 31. Примеры решения рациональных неравенств--+-6
- 32. Примеры решения рациональных неравенств+--+-112x
- 33. Примеры решения рациональных неравенствx-113+-++
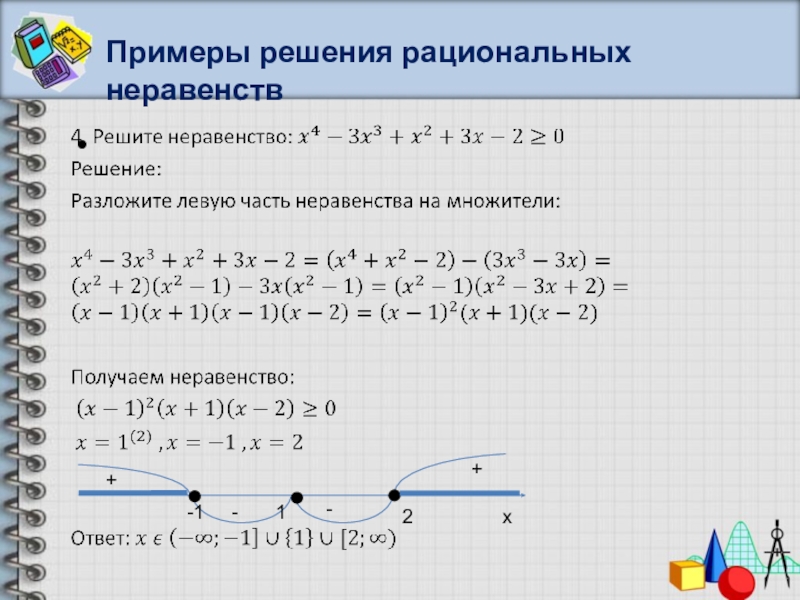
- 34. Примеры решения рациональных неравенствx+-+-+-3-113
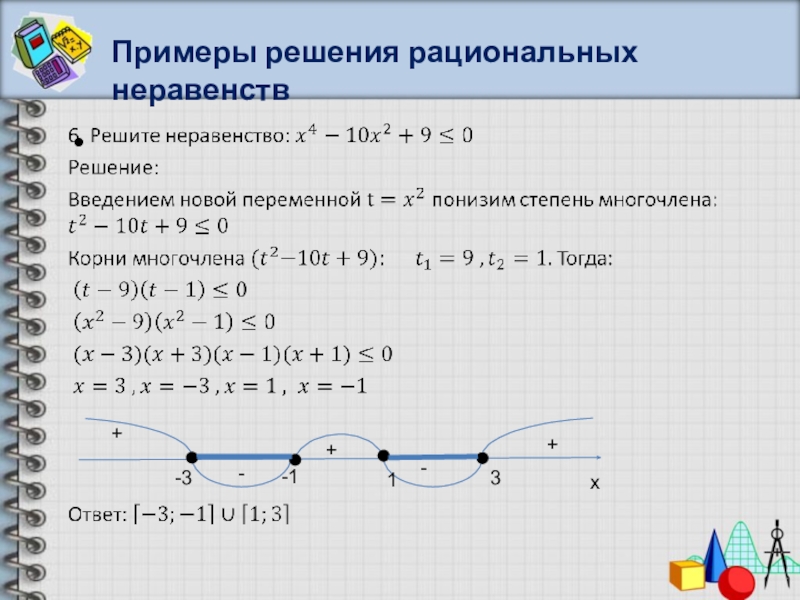
- 35. Примеры решения рациональных неравенствx+-+-10
- 36. Решение дробно-рациональных неравенств
- 37. Решение дробно-рациональных неравенств
- 38. Решение дробно-рациональных неравенств
- 39. 4) Выбрать промежутки, служащие решением данного неравенства:Если
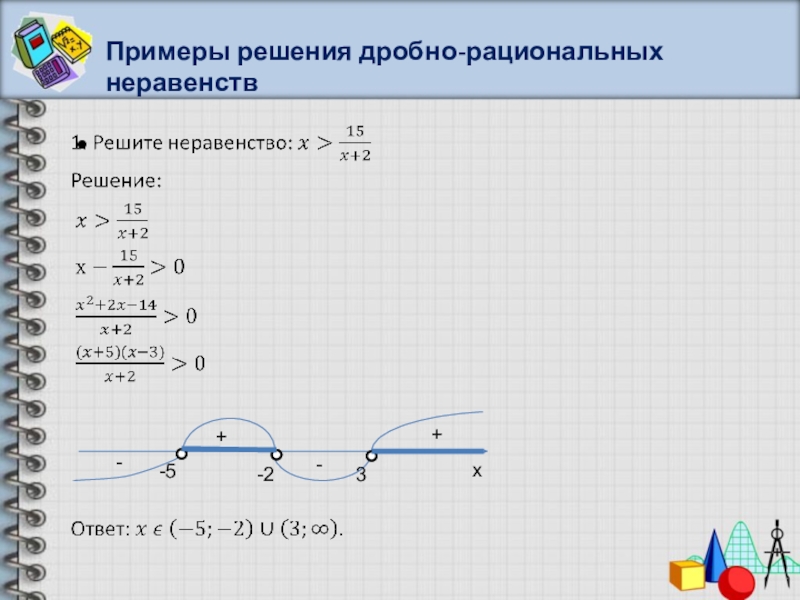
- 40. Примеры решения дробно-рациональных неравенств++-+-2-11x
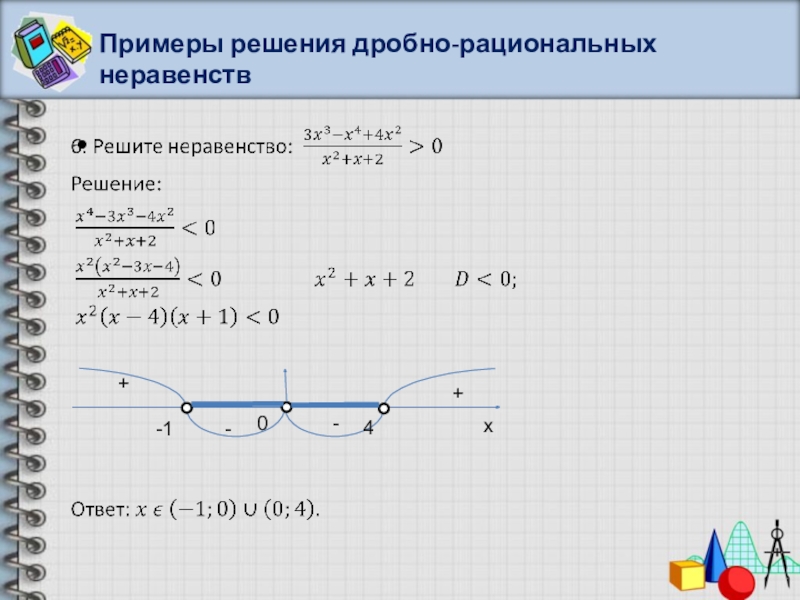
- 41. Примеры решения дробно-рациональных неравенств+--+x
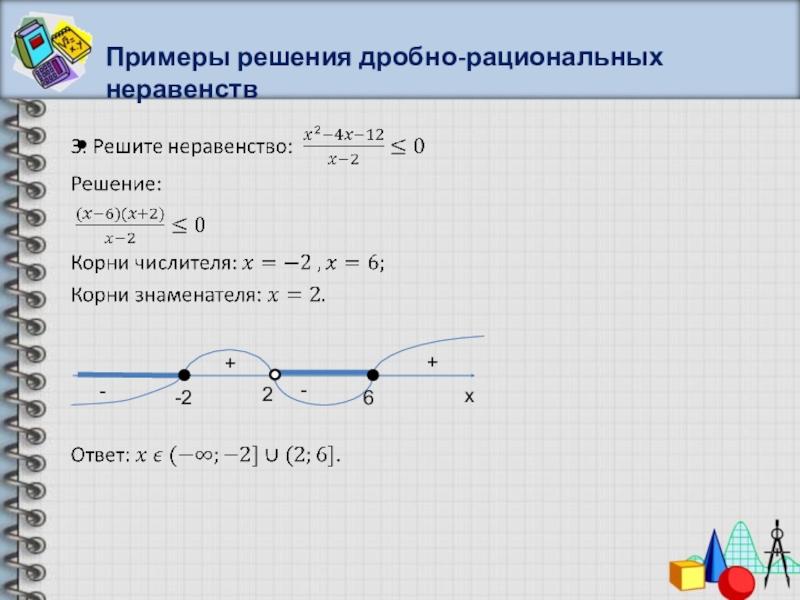
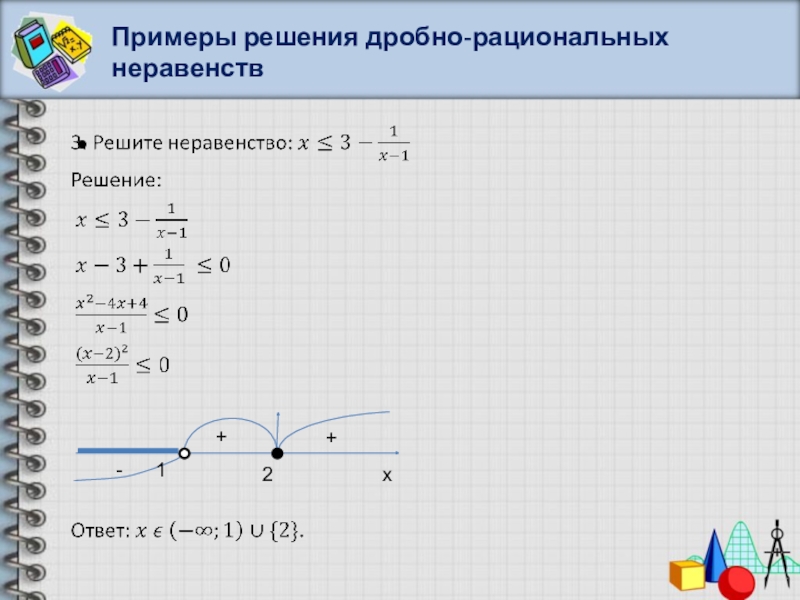
- 42. Примеры решения дробно-рациональных неравенствx-+-+-226
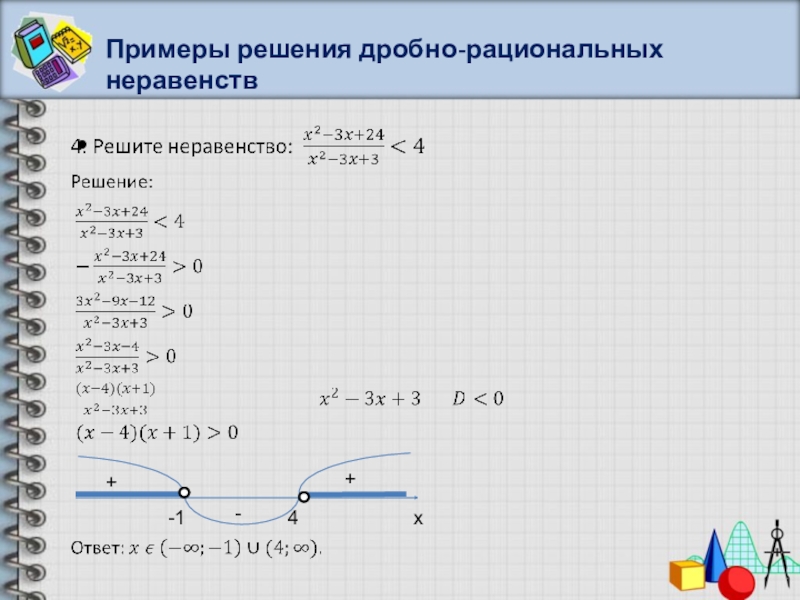
- 43. Примеры решения дробно-рациональных неравенств+--+-213x
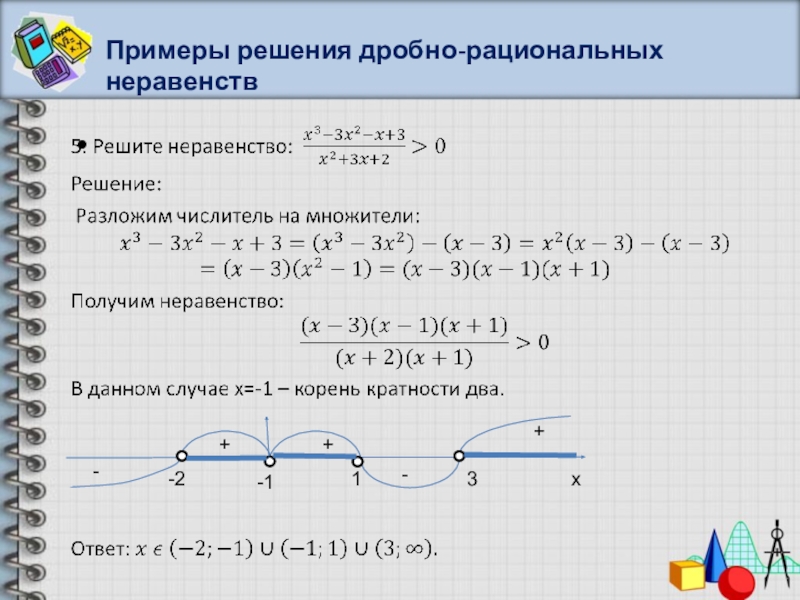
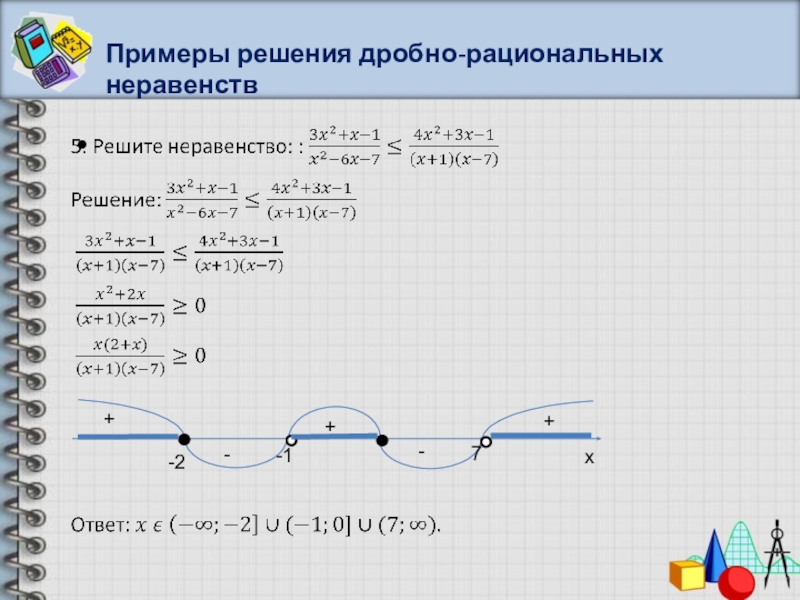
- 44. Примеры решения дробно-рациональных неравенствx-++-+-2-113
- 45. Примеры решения дробно-рациональных неравенств+--+-104x
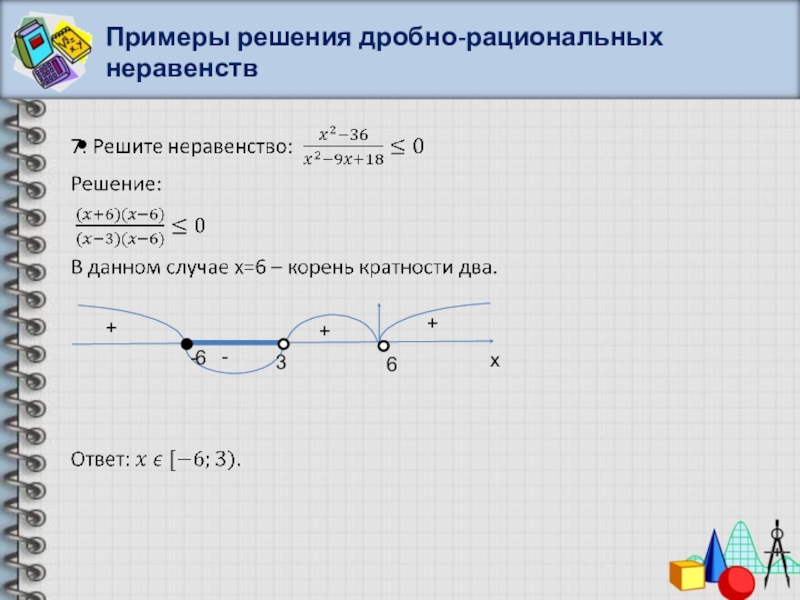
- 46. Примеры решения дробно-рациональных неравенств-+++x-636
- 47. Примеры решения дробно-рациональных неравенств++--x-2-12
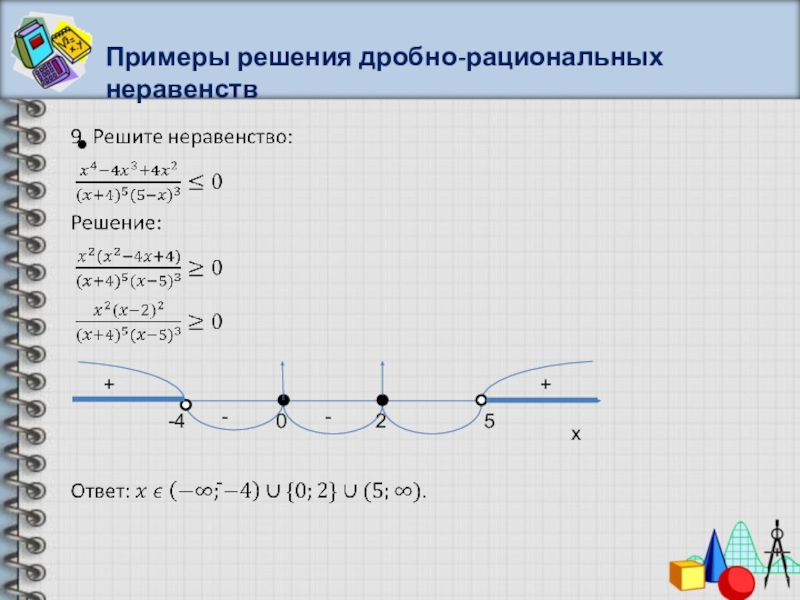
- 48. Примеры решения дробно-рациональных неравенств++----4025x
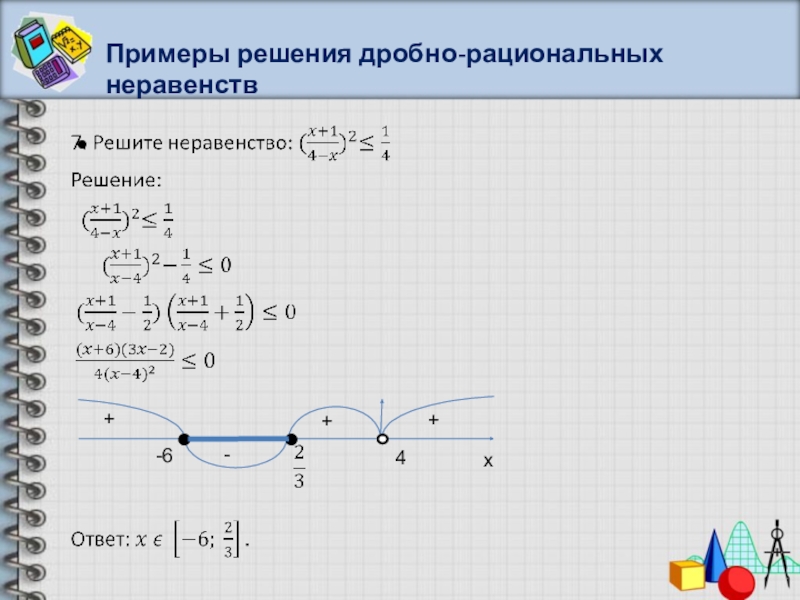
- 49. Решение дробно-рациональных неравенств
- 50. Примеры решения дробно-рациональных неравенств++--x-5-23
- 51. Примеры решения дробно-рациональных неравенств++--x-10
- 52. Примеры решения дробно-рациональных неравенств-++12x
- 53. Примеры решения дробно-рациональных неравенств++-x-14
- 54. Примеры решения дробно-рациональных неравенствx+++---2-17
- 55. Примеры решения дробно-рациональных неравенств+-++x-6 4
- 56. Примеры решения дробно-рациональных неравенств++-x-4-2
- 57. Примеры решения дробно-рациональных неравенств+++----10 12x
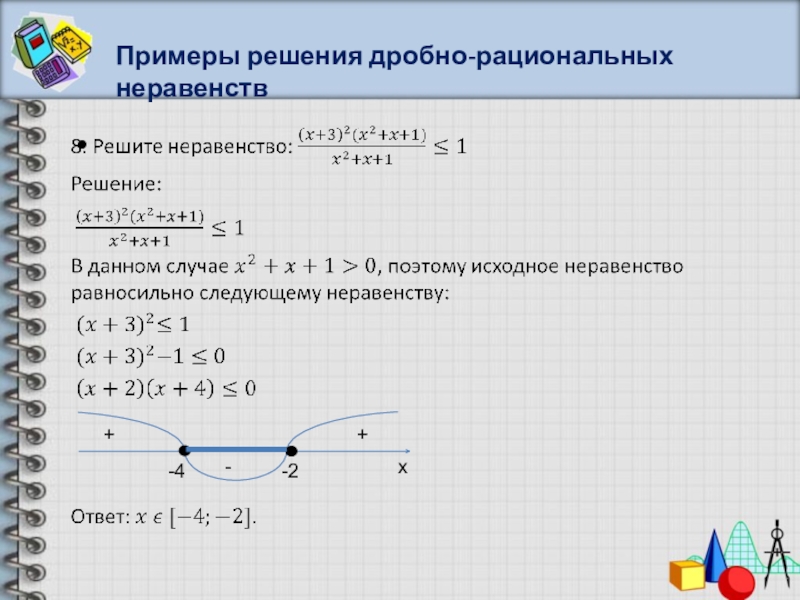
- 58. Примеры решения дробно-рациональных неравенств
- 59. Примеры решения дробно-рациональных неравенств x+++++-----2-1123467
- 60. Литература:1. Рустюмова И. П., Рустюмова С. Т.
ЦЕЛЬ УРОКА:обобщение и систематизация знаний по теме «Алгебраические неравенства»;развитие интеллектуальных способностей;воспитание ответственности, самостоятельности.
Слайд 1«Алгебраические неравенства»
Учитель математики:
Скуратова Наталья Алексеевна
ОСШЛМФИ
Усть-Каменогорск, 2014 г
Слайд 2ЦЕЛЬ УРОКА:
обобщение и систематизация знаний по теме «Алгебраические неравенства»;
развитие интеллектуальных способностей;
воспитание
ответственности, самостоятельности.
Слайд 4Свойства неравенств:
Если из одной части неравенства перенести в другую слагаемое с
противоположным знаком, то получится равносильное неравенство;
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное неравенство;
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное неравенство.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное неравенство;
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное неравенство.
Слайд 394) Выбрать промежутки, служащие решением данного неравенства:
Если неравенство строгое, ответ состоит
только из интервалов;
Если неравенство нестрогое, в ответ включают корни числителя, не являющиеся корнями знаменателя, и отдельно точки возврата, соответствующие корням числителя.
Рассмотрим применение метода интервалов на следующих примерах.
Если неравенство нестрогое, в ответ включают корни числителя, не являющиеся корнями знаменателя, и отдельно точки возврата, соответствующие корням числителя.
Рассмотрим применение метода интервалов на следующих примерах.
Решение дробно-рациональных неравенств
Слайд 60Литература:
1. Рустюмова И. П., Рустюмова С. Т. Пособие по математике для
подготовки к ЕНТ. – Алматы, 2013 г.
2. Егоркина Н. В. Абитуриенту. Математика для поступающих в ВУЗЫ. Тестовые задания, решения ответы. Серия «Домашний репетитор». – Кокшетау. – Келешек -2030, 2012 г.
3. Тавгень О. И., Тавгень А. И. Математика в задачах. Теория и методы решений. Уравнения, неравенства, системы. – Минск АВЕРСЭВ, 2005 г.
4. Литвиненко В. Н., Мордкович А. Г. Задачник-практикум по математике для поступающих в ВУЗЫ. Алгебра, тригонометрия. – Москва «Оникс 21 век» «Мир и образование» , 2005 г.
2. Егоркина Н. В. Абитуриенту. Математика для поступающих в ВУЗЫ. Тестовые задания, решения ответы. Серия «Домашний репетитор». – Кокшетау. – Келешек -2030, 2012 г.
3. Тавгень О. И., Тавгень А. И. Математика в задачах. Теория и методы решений. Уравнения, неравенства, системы. – Минск АВЕРСЭВ, 2005 г.
4. Литвиненко В. Н., Мордкович А. Г. Задачник-практикум по математике для поступающих в ВУЗЫ. Алгебра, тригонометрия. – Москва «Оникс 21 век» «Мир и образование» , 2005 г.