Учитель математики: Гулова Римма Ивановна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики Примеры комбинаторных задач. Перестановки (9 класс)
Содержание
- 1. Презентация к уроку математики Примеры комбинаторных задач. Перестановки (9 класс)
- 2. Такие задачи получили название комбинаторных
- 3. - раздел математики, в котором изучаются вопросы
- 4. Термин «комбинаторика» происходит от латинского слова «combina»,
- 5. Решить комбинаторную задачу - это значит выписать
- 6. Основные виды задач
- 7. решение методом перебора; решение с помощью
- 8. № 718.Составьте все возможные двузначные числа из
- 9. Слайд 9
- 10. 2. Решение с помощью дерева возможных вариантов
- 11. Слайд 11
- 12. 4. Решение с помощью таблиц. На завтрак
- 13. Выбор напитка – выбор объекта АВыбор каши
- 14. «Если объект А можно выбрать m способами,
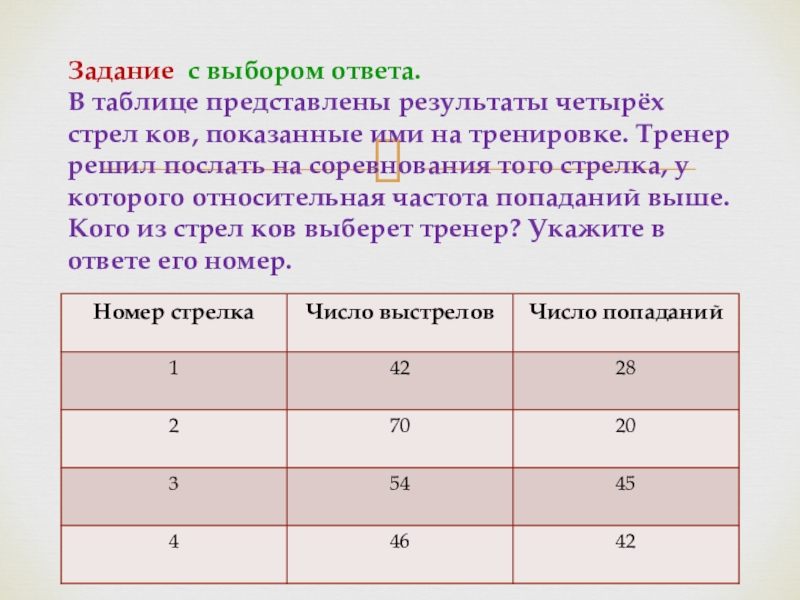
- 15. Задание с выбором ответа. В таблице представлены
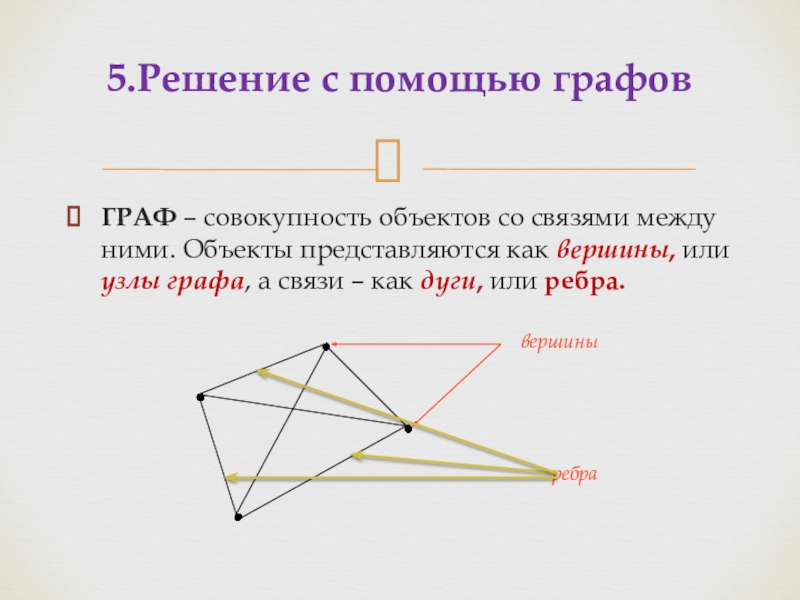
- 16. ГРАФ – совокупность объектов со связями между
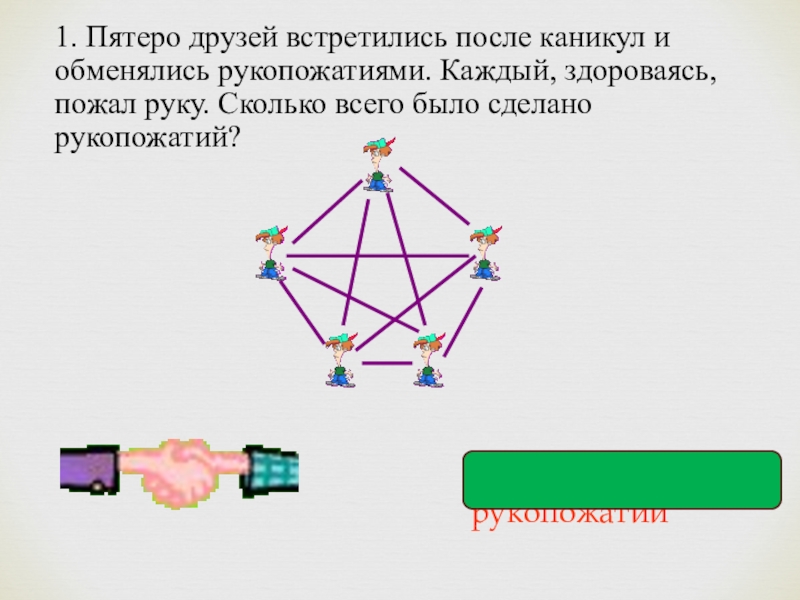
- 17. 1. Пятеро друзей встретились после каникул и
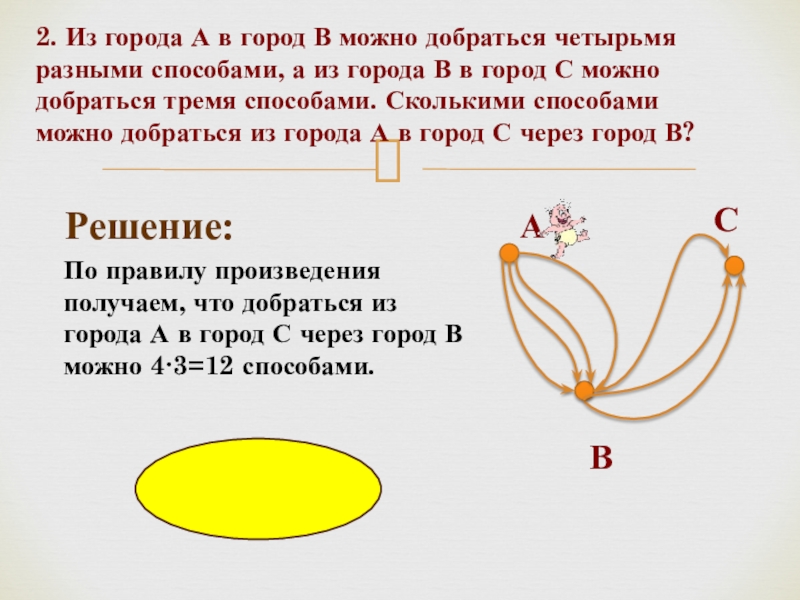
- 18. 2. Из города А в город В
- 19. Самостоятельная работа в группах Карточка № 1Задание
- 20. Самостоятельная работа в группахКарточка № 3Задание 1.В
- 21. Решение. Рассмотрим все возможные исходы жеребьёвки. · Команда А в матче
- 22. Рефлексия НА УРОКЕ Я узнал… Я научился… Мне понравилось… Я затруднялся… Моё настроение…
- 23. Спасибо за работу на уроке !
Слайд 1Решение
комбинаторных задач, перестановки
МБОУ «СОШ № 12 с УИОП» г. Старый
Слайд 2 Такие задачи получили название комбинаторных задач, а раздел математики,
В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций.
Слайд 3- раздел математики, в котором изучаются вопросы о том, сколько различных
к
о
м
б
и
н
а
т
о
р
и
к
а
Слайд 4Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на
Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Слайд 5Решить комбинаторную задачу - это значит выписать или сосчитать все возможные
Что значит решить
комбинаторную задачу?
Слайд 7
решение методом перебора;
решение с помощью дерева возможных вариантов;
решение
решение с помощью таблиц;
решение с помощью графов.
Познакомимся с некоторыми
приемами решения комбинаторных задач
Слайд 8№ 718.
Составьте все возможные двузначные числа из указанных цифр, используя в
Решение: 16, 18, 61, 68, 86, 81.
3 • 2 = 6 – правило умножения
№ 736.
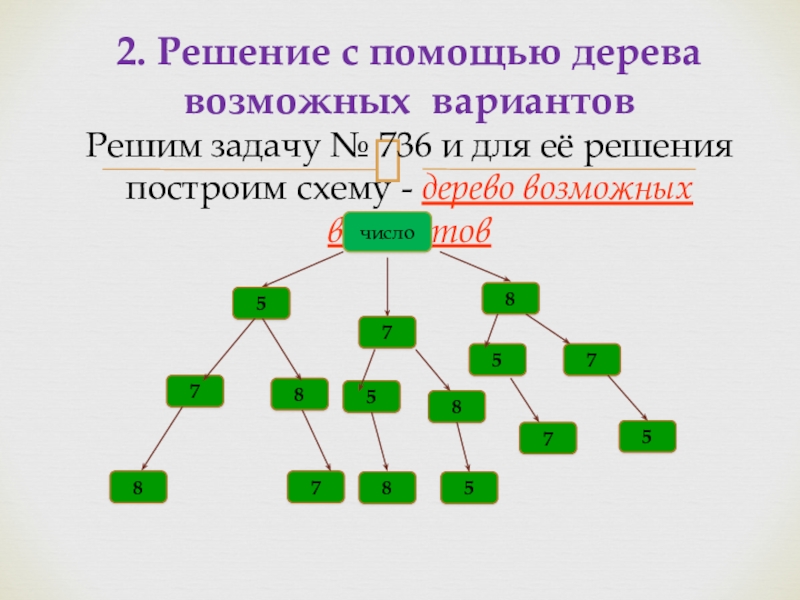
Ольга помнит, что телефон подруги оканчивается цифрами 5,7,8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.
1.Решение методом перебора
Слайд 102. Решение с помощью дерева возможных вариантов Решим задачу № 736 и
число
5
8
7
5
7
8
8
8
8
7
5
5
5
7
7
Слайд 124. Решение с помощью таблиц. На завтрак в школьной столовой можно выбрать
Слайд 13Выбор напитка – выбор объекта А
Выбор каши - выбор объекта В
Объект
вариантов выбора пары объектов А и В 3•4=12.
Слайд 14«Если объект А можно выбрать m способами, а другой объект В
Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения
Слайд 15Задание с выбором ответа. В таблице представлены результаты четырёх стрел ков, показанные
Слайд 16ГРАФ – совокупность объектов со связями между ними. Объекты представляются как
5.Решение с помощью графов
вершины
ребра
Слайд 171. Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь,
Ответ:10 рукопожатий
Слайд 182. Из города А в город В можно добраться четырьмя разными
Ответ: 12
Решение:
По правилу произведения получаем, что добраться из города А в город С через город В можно 4∙3=12 способами.
А
В
С
Слайд 19Самостоятельная работа в группах
Карточка № 1
Задание 1. Коля выбирает трехзначное число.
Задание 2.
Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
Задание 3.
В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Задание 4.
В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Карточка № 2
Задание 1.
Стас, Денис, Костя, Маша, Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
Задание 2.
В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3
спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
Задание 3.
Из каждых 1000 электрических лампочек 5 бракованных. Какова вероятность купить исправную лампочку?
Задание 4.
Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
Слайд 20Самостоятельная работа в группах
Карточка № 3
Задание 1.
В случайном эксперименте симметричную монету
Задание 2.
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
Задание 3.
В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
Задание 4.
В среднем из 100 карманных фонариков, поступивших в продажу, восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Карточка № 4
Задание 1.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих мат чах первой мячом будет владеть команда А.
Задание 2.
Средний рост жителя города, в котором живет Даша, равен 170 см. Рост Даши 173 см. Какое из следующих утверждений верно?
1) Даша — самая высокая девушка в городе.
2) Обязательно найдется девушка ниже 170 см.
3) Обязательно найдется человек ростом менее 171 см.
4) Обязательно найдется человек ростом 167 см.
Задание 3.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задание 4.
Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
Слайд 21Решение.
Рассмотрим все возможные исходы жеребьёвки.
· Команда А в матче в обоих матчах первой
· Команда А в матче в обоих матчах не владеет мячом первой.
· Команда А в матче с командой В владеет мячом первой, а в матче с командой С — второй.
· Команда А в матче с командой С владеет мячом первой, а в матче с командой В — второй.
Из четырех исходов один является благоприятным, вероятность его наступления равна 0,25.
Разбор решения: Карточка № 4. Задание 1.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих мат чах первой мячом будет владеть команда А.