- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентации на тему Элементы комбинаторики, статистики и теории вероятностей
Содержание
- 1. Презентации на тему Элементы комбинаторики, статистики и теории вероятностей
- 2. Комбинаторика – это раздел математики, в котором
- 3. Готфрид Вильгельм Лейбниц (1.07.1646 - 14.11.1716)Комбинаторику, как
- 4. Значительный вклад в развитие комбинаторики внес Леонард
- 5. Методы решения комбинаторных задач Правило суммы. Правило произведения. Таблицы. Графы (деревья). Формулы.
- 6. Правило суммы Если элемент А может быть
- 7. Правило произведения Если элемент А может быть
- 8. в) Сколько среди них чисел, кратных 11?Решение:
- 9. Задача 3. Сколько существует способов занять 1-ое,
- 10. Задача 4. Сколько различных двузначных чисел можно
- 11. Задача 5. Несколько стран в качестве символа
- 12. в) Сколько всего стран могут использовать такую
- 13. Задача 6. Сколькими способами можно посадить шестерых
- 14. Пусть Коля сидит на краю. Место на
- 15. Задача 7. На входной двери дома установлен
- 16. Задача 8. В контрольной работе будет 5
- 17. Таблицы вариантовСоставляя расписание уроков на понедельник для
- 18. Сколько двузначных чисел, кратных 3, можно получить
- 19. Подсчет вариантов с помощью графовПри встрече каждый
- 20. Дерево вариантовСколько различных двухзначных чисел можно записать,
- 21. Формулы Правило умножения позволяет в один шаг
- 22. Выбор нескольких элементов. Сочетания.
- 23.
- 24. Рассмотрим пример, в котором используется и правило умножения, и теорема о числе сочетаний.
Слайд 2Комбинаторика – это раздел математики, в котором изучаются вопросы о том,
С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.
Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.
Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
Слайд 3Готфрид Вильгельм Лейбниц
(1.07.1646 - 14.11.1716)
Комбинаторику, как самостоятельный раздел математики первым
Слайд 4Значительный вклад в развитие комбинаторики внес Леонард Эйлер (1707-1783)
Он рассматривал
Слайд 5Методы решения комбинаторных задач
Правило суммы.
Правило произведения.
Таблицы.
Графы (деревья).
Слайд 6Правило суммы
Если элемент А может быть выбран К1 способами, а элемент
Задача 1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?
Решение: К1=5 –кратное 2 (2,4,16,20,28),
К2=4 – кратное 3 (3,15,21,75)
К1+К2 = 5+4 = 9
Слайд 7Правило произведения
Если элемент А может быть выбран К1 способами, а элемент
Задача 2. а) Сколько различных двузначных чисел можно составить из цифр 1, 3, 5, 7, 9?
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
N= 5х1 =5
Слайд 8в) Сколько среди них чисел, кратных 11?
Решение: Двузначное число кратно 11,
г) Сколько среди них чисел, кратных 3?
Решение: Число кратно 3, если сумма его цифр делится на 3. Составим всевозможные пары:
1 – 1 3 – 3 5 – 5 7 – 7 9 – 9
1 – 3 3 – 5 5 – 7 7 – 9
1 – 5 3 – 7 5 – 9
1 – 7 3 – 9
1 – 9
Таких пар 15. Среди них 5 пар, сумма которых делится на 3, причем три пары допускают перестановку, т.е. могут образовать по два разных числа. Всего 5+3=8 различных двузначных чисел.
Слайд 9Задача 3. Сколько существует способов занять 1-ое, 2-ое и 3-е места
а) 10 команд?
Решение: N=10х9х8=720
б) 11 команд?
Решение: N=11х10х9=990
Слайд 10Задача 4. Сколько различных двузначных чисел можно составить из цифр
а) цифры не повторяются?
Решение: На первом месте одна из 4-х цифр ( 0 не может быть), на 2-ом – одна из оставшихся 4-х:
N=4х4= 16
б) цифры могут повторяться
Решение: На 1-ом месте может быть одна из 4-х цифр, на 2-ом – одна из 5 (0 входит):
N=4х5= 20
Слайд 11Задача 5. Несколько стран в качестве символа своего государства решили использовать
а)Сколько всего стран могут использовать такую символику?
Решение: Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N=4х3х2х1=24
Слайд 12в) Сколько всего стран могут использовать такую символику с нижней белой
Решение: Если фиксировать цвет нижней полосы, то цвета трех расположенных над ней полос можно выбрать 3х2х1 = 6 способами
г) Сколько стран могут использовать такую символику с верхней белой полосой?
Решение: Если фиксировать цвет белой полосы, то цвета следующих полос можно выбрать 3х2х1 = 6 способами.
Слайд 13Задача 6. Сколькими способами можно посадить шестерых школьников на скамейку так,
Решение: Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
Слайд 14Пусть Коля сидит на краю. Место на краю можно выбрать 2
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего 4х2х4х3х2х1=192 способами.
По правилу сложения 48+192= 240 способов
Слайд 15Задача 7. На входной двери дома установлен домофон, на котором нанесены
Решение: Выбор 1-й цифры – 10 вариантов, 2-й –10 вариантов.
Всего 10х10 – 1 = 99 вариантов
Ответ: хватит.
Слайд 16Задача 8. В контрольной работе будет 5 задач – по одной
а) общее число всех возможных вариантов контрольной работы
Решение: Каждая задача может быть выбрана 10 способами. По правилу произведения N=10х10х10х10х10=100000
б) число тех вариантов, в которых Вова умеет решать все 5 задач
Решение: N=8х8х8х8х8=32768
в) число тех вариантов, в которых Вова не сможет решить ни одной задачи
Решение: N=2х2х2х2х2=32
г) число тех вариантов, в которых Вова умеет решать все задачи, кроме первой.
Решение: N=2х8х8х8х8=8192
Слайд 17Таблицы вариантов
Составляя расписание уроков на понедельник для 9б класса, завуч хочет
Решение: Составим таблицу вариантов:
Всего существует 2х3 = 6 вариантов
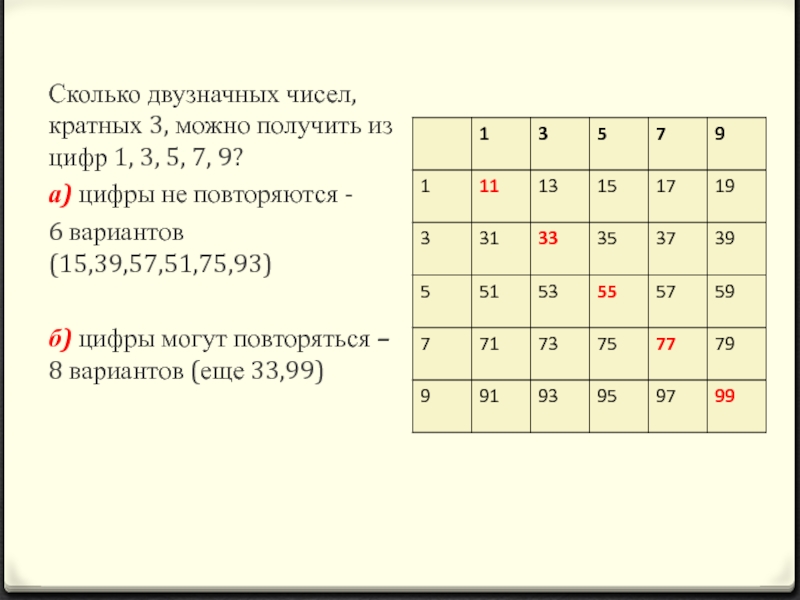
Слайд 18Сколько двузначных чисел, кратных 3, можно получить из цифр 1, 3,
а) цифры не повторяются -
6 вариантов (15,39,57,51,75,93)
б) цифры могут повторяться – 8 вариантов (еще 33,99)
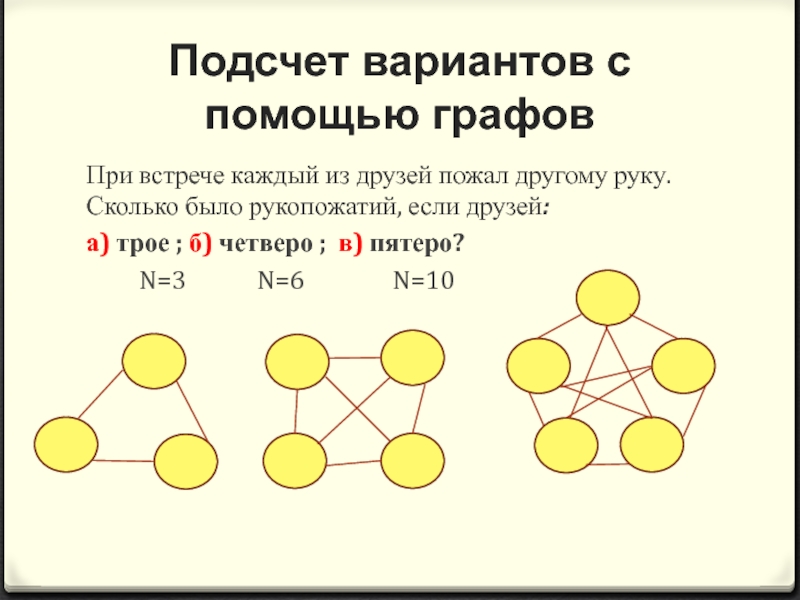
Слайд 19Подсчет вариантов с помощью графов
При встрече каждый из друзей пожал другому
а) трое ; б) четверо ; в) пятеро?
N=3 N=6 N=10
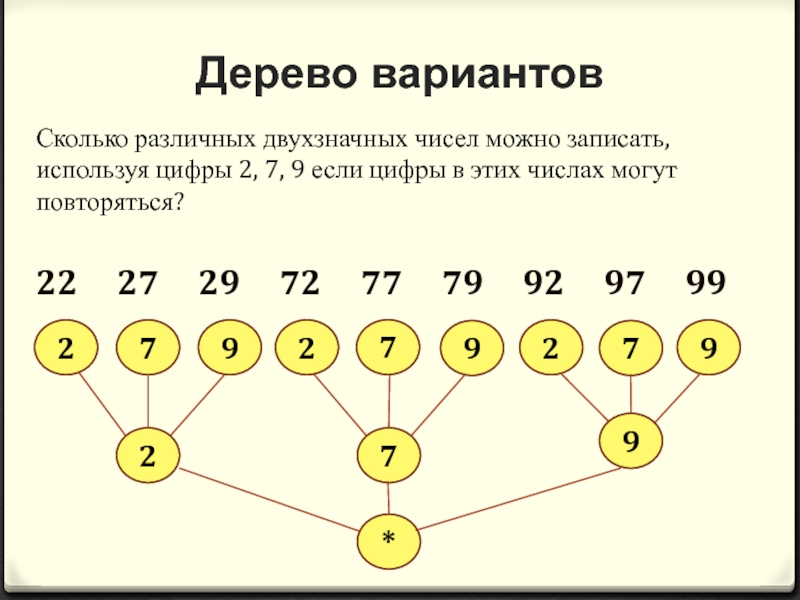
Слайд 20Дерево вариантов
Сколько различных двухзначных чисел можно записать, используя цифры 2, 7,
22 27 29 72 77 79 92 97 99
9
2
7
9
7
7
9
*
2
2
7
9
2
Слайд 21Формулы
Правило умножения позволяет в один шаг решать самые разнообразные задачи.
Определение: произведение первых подряд идущих n натуральных чисел обозначают n! (читается «эн факториал»)
n! = 1 х 2 х 3 х … х (n-2) x (n-1) x n.
Число перестановок множества из n элементов
Pn = n!