Русский математик XIX века П.Л.Чебышёв
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Наибольшее и наименьшее значения функции на отрезке ( 10 класс)
Содержание
- 1. Наибольшее и наименьшее значения функции на отрезке ( 10 класс)
- 2. 1. Найти наибольшее значение функции по её
- 3. 2. Найти наименьшее значение функции по её
- 4. 3. Какие точки называются стационарными?4. Какие точки
- 5. Нахождение наибольшего и наименьшего значений функции
- 6. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке10 класс
- 7. ° ВЫВЕСТИ АЛГОРИТМ НАХОЖДЕНИЯ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО
- 8. yyxx000аааbbbY= f(x)Y= f(x)Y= f(x)Функция у = f(х)
- 9. Выводы 1.Если
- 10. Найти наибольшее и наименьшее значение функции у
- 11. Найти наибольшее и наименьшее значение функции у
- 12. Алгоритм нахождения наибольшего и наименьшего значений непрерывной
- 13. а) если х = хо – точка
- 14. СПАСИБО ЗА УРОК
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]542-5у наиб. = 4[-5; 6]у наиб. = 5[-7; 6]11
Слайд 1 ”Особенную важность имеют те методы науки, которые позволяют решать задачу,
общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды”.
Слайд 21. Найти наибольшее значение функции по её графику
на [ -5;6] и [-7; 6]
5
4
2
-5
у наиб. = 4
[-5; 6]
у наиб. = 5
[-7; 6]
1
1
![1. Найти наибольшее значение функции по её графику на [ -5;6]](/img/thumbs/e80dd33f0efc45f6683bc6724f86153f-800x.jpg "Наибольшее и наименьшее значения функции на отрезке ( 10 класс) 1. Найти наибольшее значение функции по её графику")
Слайд 32. Найти наименьшее значение функции по её графику
на [ -7;4] и [-7; 6]
у наим. =- 3
[-7; 4]
у наим. = -4
[-7; 6]
-3
-2
4
-4
![2. Найти наименьшее значение функции по её графику на [ -7;4] и](/img/thumbs/d4c57663c6af9832ebc0f7b27509a445-800x.jpg "Наибольшее и наименьшее значения функции на отрезке ( 10 класс) 2. Найти наименьшее значение функции по её графику на")
Слайд 43. Какие точки называются
стационарными?
4. Какие точки называются
критическими?
5. Назвать необходимые
и достаточные условия существования точек экстремума функции
Слайд 5 Нахождение наибольшего и наименьшего значений функции широко применяется при решении
многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, в так называемых задачах на оптимизацию.
ПРИМЕР. Рекламный щит имеет форму прямоугольника S=9 м2. Изготовьте щит в виде прямоугольника с наименьшим периметром
Слайд 7° ВЫВЕСТИ АЛГОРИТМ НАХОЖДЕНИЯ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ. °
РЕШАТЬ ЗАДАЧИ НА ОТЫСКАНИЕ НАИБОЛЬШИХ И НАИМЕНЬШИХ ЗНАЧЕНИЙ ФУНКЦИИ.
Цели урока:
Слайд 8y
y
x
x
0
0
0
а
а
а
b
b
b
Y= f(x)
Y= f(x)
Y= f(x)
Функция у = f(х) непрерывна на отрезке [a;b].
Найти наибольшее и наименьшее значение функций, графики которых предоставлены на рисунках.
Сделать вывод о расположении точек, в которых
функция достигает наибольшего(наименьшего)
значений
![yyxx000аааbbbY= f(x)Y= f(x)Y= f(x)Функция у = f(х) непрерывна на отрезке [a;b]. Найти наибольшее и наименьшее значение функций,](/img/thumbs/2a7f9560ed665da6dfaa5061884132f5-800x.jpg "Наибольшее и наименьшее значения функции на отрезке ( 10 класс) yyxx000аааbbbY= f(x)Y= f(x)Y= f(x)Функция у = f(х) непрерывна на отрезке [a;b].")
Слайд 9
Выводы
1.Если функция непрерывна на отрезке, то она достигает на нем и
своего наибольшего, и своего наименьшего значений.
2.Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3.Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Слайд 10
Найти наибольшее и наименьшее значение функции у = х³ - 3х²
- 45х + 1 на [-4; 6]
без построения графика.
без построения графика.
Задание 1.
Слайд 11
Найти наибольшее и наименьшее значение функции у = х³ - 5х²
+ 7х на [-1; 2]
без построения графика.
без построения графика.
Задание 2.
Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3
![Найти наибольшее и наименьшее значение функции у = х³ - 5х² + 7х на [-1; 2] без](/img/thumbs/1191386dcec3085e51cd9c02031a2540-800x.jpg "Наибольшее и наименьшее значения функции на отрезке ( 10 класс) Найти наибольшее и наименьшее значение функции у = х³ - 5х²")
Слайд 12Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x)
на отрезке [a;b]
1. Найти производную f´(х)
2. Найти стационарные и критические точки функции, лежащие внутри oтрезка [a;b]
3. Вычислить значение функции у= f(x) в точках,
отобранных на втором шаге, и в точках a и b.
Выбрать среди этих значений наименьшее
( это будет унаим )и наибольшее (это будет унаиб )
![Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x) на отрезке [a;b]1. Найти производную](/img/thumbs/350f54a69622422f8f0cbe8f967fd924-800x.jpg "Наибольшее и наименьшее значения функции на отрезке ( 10 класс) Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у = f(x)")
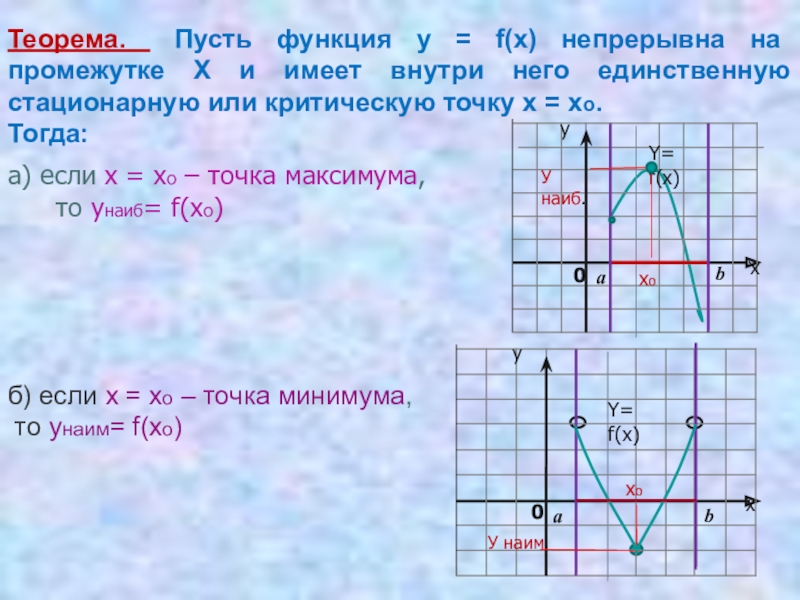
Слайд 13а) если х = хо – точка максимума,
то унаиб= f(xo)
Теорема.
Пусть функция у = f(x) непрерывна на промежутке Х и имеет внутри него единственную стационарную или критическую точку х = хо.
Тогда:
Тогда:
б) если х = хо – точка минимума,
то унаим= f(xo)
