СЕЙДИНА А.З.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Математика пәні презентация Виет теоремасы 8 сынып
Содержание
- 1. Математика пәні презентация Виет теоремасы 8 сынып
- 2. Сабақ мақсаты:
- 3. Үй тапсырмасы:№ 1391)D=0 бір түбірі бар
- 4. Слайд 4
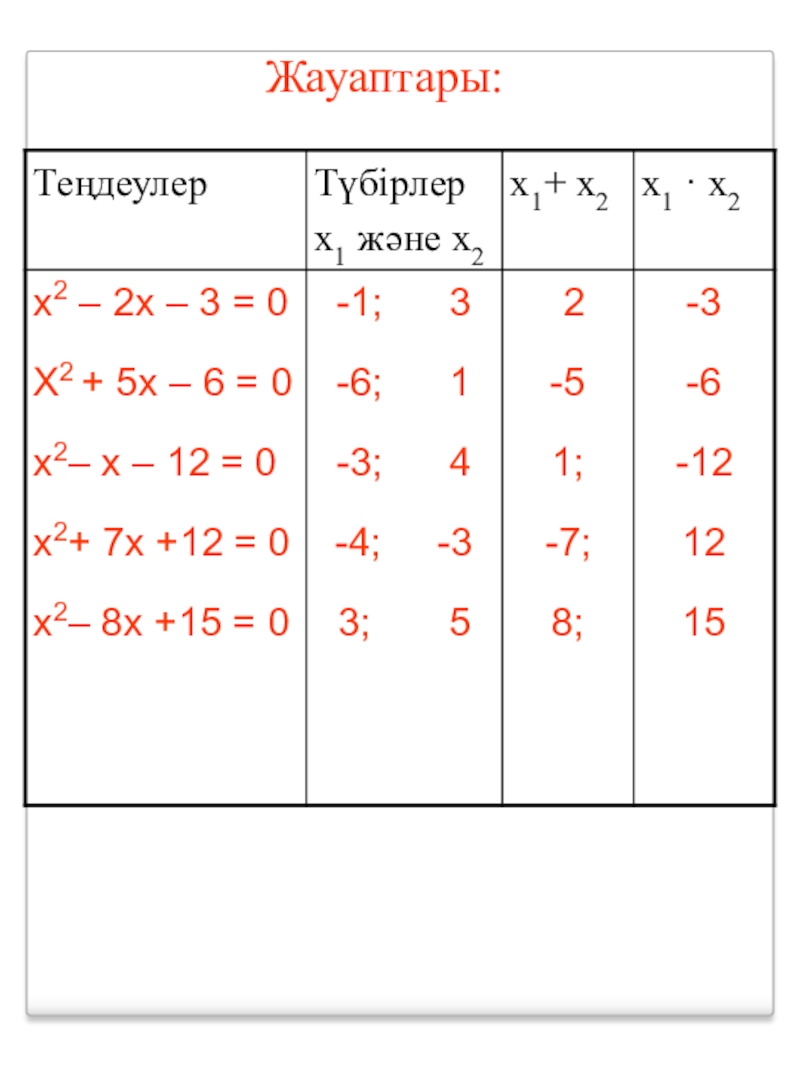
- 5. Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің мәндерін табыңдар.
- 6. Жауаптары:
- 7. Бұл мысалдардан, келтірілген квадраттық
- 8. Слайд 8
- 9. Бұл теореманы бірінші дәлелдеген француз математигі Француа
- 10. Теорема ( Виет теоремасына кері теорема).
- 11. Виет теоремасы және оған
- 12. №147
- 13. №151
- 14. №156. Түбірлері
- 15. 1. х2 - 12х + с
- 16. Тест сұрақтары:Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін
- 17. ВИЕТ
- 18. Теңдеулердің түбірлерінің қосындысы мен көбейтіндісін табыңдар:1) Х
- 19. ҮЙГЕ ТАПСЫРМА: §8. №148, №157,№159 54-55 БЕТ
Сабақ мақсаты: 1. Виет теоремасын тұжырымдау және дәлелдеу. Квадрат теңдеулерді түбірлердің қасиеттерін қолдану арқылы шешуді үйрету; 2. Оқушыларға Виет теоремасын қолдану тәсілдерімен таныстыру және квадрат теңдеулерді шешуді үйрету; 3.
Слайд 2 Сабақ мақсаты: 1. Виет теоремасын тұжырымдау және дәлелдеу. Квадрат теңдеулерді түбірлердің
қасиеттерін қолдану арқылы шешуді үйрету;
2. Оқушыларға Виет теоремасын қолдану тәсілдерімен таныстыру және квадрат теңдеулерді шешуді үйрету;
3. Виет теоремасын қолдана отырып есептер шығаруға оқушыларды баулу және дағдыландыру.
Слайд 3Үй тапсырмасы:
№ 139
1)D=0 бір түбірі бар 5) D>0 Екі
түбірі бар
2) D<0 түбірі жоқ 6) D>0 Екі түбірі бар
3) D>0 екі түбірі бар 7) D>0 Екі түбірі бар
4) D<0 Түбірі жоқ 8) D>0 Екі түбірі бар
№140
1)Х1 = - 7,15 3) Х1 = - 4,38 5) Х1 = -1,17
Х2 = - 0,35 Х2 = -0,42 Х2 = -0,42
2)Х1 = - 1,79 4) Х1 = 7,2 6) Х1 = -0,09
Х2 = 0,37 Х2 = 3,34 Х2 = 1,75
2) D<0 түбірі жоқ 6) D>0 Екі түбірі бар
3) D>0 екі түбірі бар 7) D>0 Екі түбірі бар
4) D<0 Түбірі жоқ 8) D>0 Екі түбірі бар
№140
1)Х1 = - 7,15 3) Х1 = - 4,38 5) Х1 = -1,17
Х2 = - 0,35 Х2 = -0,42 Х2 = -0,42
2)Х1 = - 1,79 4) Х1 = 7,2 6) Х1 = -0,09
Х2 = 0,37 Х2 = 3,34 Х2 = 1,75
Слайд 4
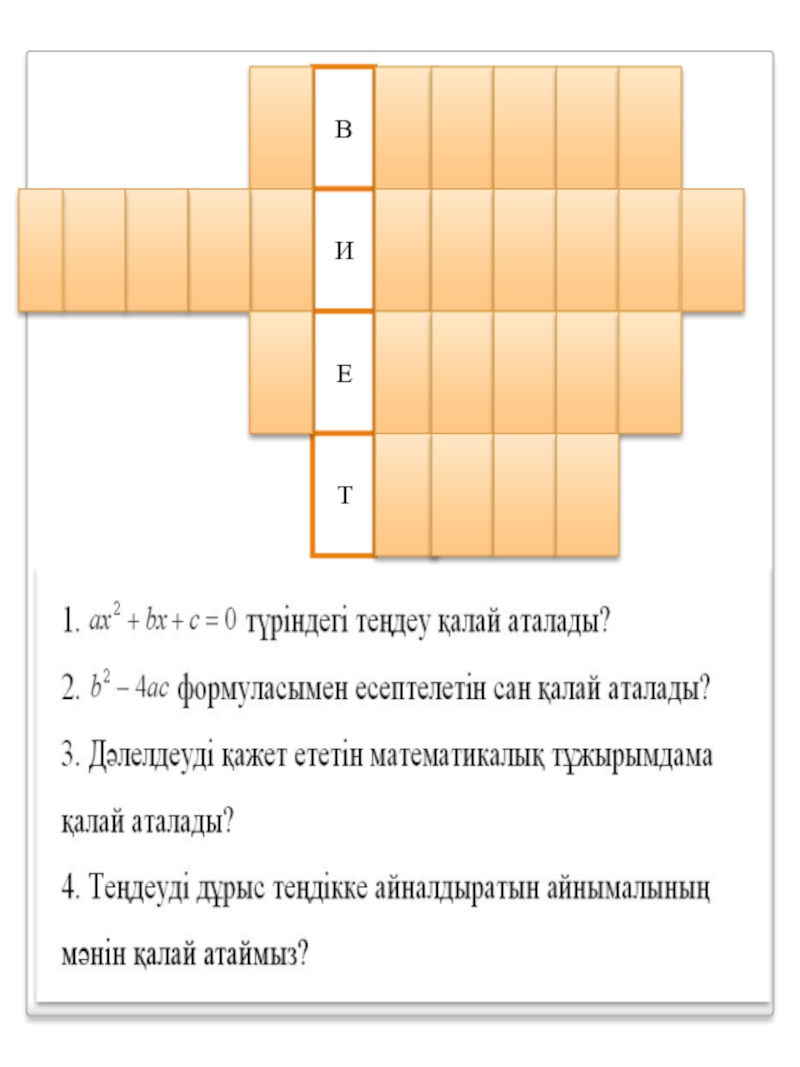
түріндегі теңдеу қалай аталады?
формуласымен есептелетін сан қалай аталады?
3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі болады?
4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі болады?
5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады?
6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық теңдеу деп атайды?
7. теңдеуінің коэффициенттерін атап шығыңдар.
8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с немесе
b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды?
формуласымен есептелетін сан қалай аталады?
3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі болады?
4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі болады?
5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады?
6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық теңдеу деп атайды?
7. теңдеуінің коэффициенттерін атап шығыңдар.
8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с немесе
b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды?
Слайд 5 Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен
көбейтіндісінің мәндерін табыңдар.
Слайд 7 Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы
таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап шығайық.
Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады:
Енді бұл қасиетті теорема ретінде тұжырымдап шығайық.
Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады:
Слайд 8
(келтірілген квадрат теңдеу)
– екінші коэффициент
– бос мүше
Теңдеудің дискриминанті:
Егер D>0, онда теңдеудің екі түбірі бар:
Түбірлердің қосындысы:
Түбірлердің көбейтіндісі:
Сонымен,
– екінші коэффициент
– бос мүше
Теңдеудің дискриминанті:
Егер D>0, онда теңдеудің екі түбірі бар:
Түбірлердің қосындысы:
Түбірлердің көбейтіндісі:
Сонымен,
Слайд 9Бұл теореманы бірінші дәлелдеген француз математигі Француа Виет (1540-1603) болғандықтан, соның
атымен аталады.
Өзінің алгебралық ойларын Виет “Аналитикалық шеберлікке кіріспе” шығармасында жазған.Онда алгебраны математикалық есептеу әдісіне айналдыруды ұсынған Виет: “Барлық математик ғалымдар алгебрада теңдесі жоқ қазына бар екенін білген,бірақ қазынаны табуды білмеді.Олардың неғұрлым күрделі деп тапқан есептері біздің шеберлік арқылы оңай шешіледі”, - деп жазған.
Өзінің алгебралық ойларын Виет “Аналитикалық шеберлікке кіріспе” шығармасында жазған.Онда алгебраны математикалық есептеу әдісіне айналдыруды ұсынған Виет: “Барлық математик ғалымдар алгебрада теңдесі жоқ қазына бар екенін білген,бірақ қазынаны табуды білмеді.Олардың неғұрлым күрделі деп тапқан есептері біздің шеберлік арқылы оңай шешіледі”, - деп жазған.
Слайд 10 Теорема ( Виет теоремасына кері теорема).
Егер екі
санның қосындысы – р-ға, ал олардың
көбейтіндісі q-ға тең болса,онда ол сандар
х² + рх + q = 0 теңдеуінің түбірлері болады.
көбейтіндісі q-ға тең болса,онда ол сандар
х² + рх + q = 0 теңдеуінің түбірлері болады.
Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады.
Слайд 11 Виет теоремасы және оған кері теорема теңдеуді шешпей-ақ
, түбірлерінің қосындысы мен көбейтіндісін табуға және түбірлері белгілі болғанда, теңдеуді құруға мүмкіндік береді.
Мысал қарастырайық: Түбірлері және
болған квадраттық теңдеуді құрайық:
Мысал қарастырайық: Түбірлері және
болған квадраттық теңдеуді құрайық:
Слайд 15
1. х2 - 12х + с = 0 теңдеуінің бір
түбірі х1=5.
х1+ х2=12 және х1 · х2=с. с-ны табыңдар.
2.х2 +рх + 15 = 0 теңдеуінің бір түбірі х1=3.
х1+ х2= -р және х1 · х2=15. р-ны табыңдар.
3. Теңдеулерді шешіп Виет теоремасы және кері теорема арқылы тексеріңдер:
а) х2 - 9х + 8 = 0,
б) х2 + 12х + 20 = 0,
в) х2 - 4х - 21 = 0.
х1+ х2=12 және х1 · х2=с. с-ны табыңдар.
2.х2 +рх + 15 = 0 теңдеуінің бір түбірі х1=3.
х1+ х2= -р және х1 · х2=15. р-ны табыңдар.
3. Теңдеулерді шешіп Виет теоремасы және кері теорема арқылы тексеріңдер:
а) х2 - 9х + 8 = 0,
б) х2 + 12х + 20 = 0,
в) х2 - 4х - 21 = 0.
Слайд 16Тест сұрақтары:
Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
А) 8; 15 В) -3; 5 С) 3 ;5 D) -5; -3 Е) 5; -8
2. Түбірлері болатын теңдеуді жазыңдар:
А) В) С)
D) Е)
теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және р-ны табыңдар.
А) 7; 5 В) -2; -5 С) -7; -2 D) -7;5 Е) 5; -1.
4. Теңдеудің түбірлерін табыңдар:
А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10
5. Келтірілген квадраттық теңдеуді көрсет:
А) В) С)
D) Е)
Слайд 18Теңдеулердің түбірлерінің
қосындысы мен көбейтіндісін табыңдар:
1) Х ² + х –
2 = 0
2) Х ² +х – 20 = 0
3) X² + х – 6 = 0
4) Х² + х – 42 =0
5) Х ² +3х –18 = 0
6) Х ² + 2х – 48=0
7) Х ² +х – 12 = 0
8) Х ² + 3х – 4=0
2) Х ² +х – 20 = 0
3) X² + х – 6 = 0
4) Х² + х – 42 =0
5) Х ² +3х –18 = 0
6) Х ² + 2х – 48=0
7) Х ² +х – 12 = 0
8) Х ² + 3х – 4=0
-3; 2
-7; 6
3) -8;6
-1;2
5) -5;4
6) -4;3
7) -6;3
8) -4;1