- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Логарифмическая функция, ее свойства и график
Содержание
- 1. Логарифмическая функция, ее свойства и график
- 2. О сколько нам открытий чудныхГотовят просвещенье духИ опыт, сын ошибок трудных,И гений, парадоксов друг…
- 3. 1.Устная работаНЕПРЕ
- 4. Дата рождения:
- 5. 2. Задание на соответствие.Каждому графику поставьте в соответствие функцию5
- 6. Вариант 2 Вариант 1Задание 4. Вычислите, если возможно.
- 7. Вариант 2-2; -1; 0; 1; 2; 4;
- 8. Вариант 2 Вариант 1Задание 4. Вычислите, если возможно.
- 9. Слайд 9
- 10. Функция y = loga x, её свойства и график.
- 11. Леонард Эйлернем. Leonhard EulerДата рождения: 4 (15) апреля
- 12. 1) D(f) – область определения функции.2) Чётность
- 13. Постройте графики функций:1 вариант2 вариант
- 14. xy01231248- 1- 2- 3Проверка:График логарифмическойфункции называютлогарифмической кривой.
- 15. xy01231248- 1- 2График функции y = loga
- 16. 1) D(f) = (0, + ∞);2) не
- 17. 1) D(f) = (0, + ∞);2) не
- 18. Слайд 18
- 19. Какие из следующих графиков не могут быть графиком y =
- 20. Задание №1Найдите наибольшее и наименьшее значения функции
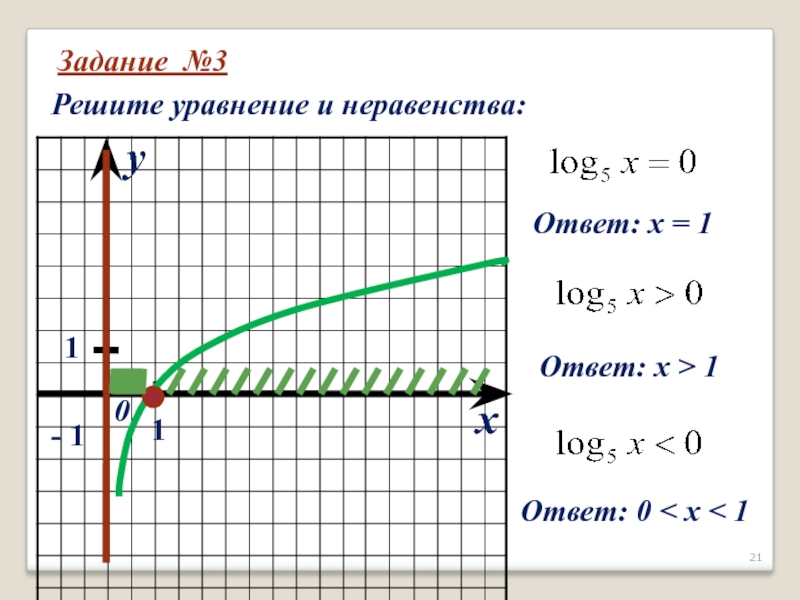
- 21. Задание №3Решите уравнение и неравенства:xy011- 1 Ответ:
- 22. Самостоятельно:Решите уравнение и неравенства:Ответ: х = 1Ответ: х > 1Ответ: 0 < х < 1
- 23. Выполнение упражнений№ 79 (1,3), 77 (1,3), 78 (1,3,5)
- 24. Область определения логарифмической функции – вся числовая
- 25. Логарифмическая функция не является ни чётной, ни
- 26. Гл.VII,§ 4 №74, 82, 83 по группамДополнительно: с помощью Интернет-ресурсов найти области применения логарифмической функции.
- 27. Слайд 27
Слайд 2О сколько нам открытий чудных
Готовят просвещенье дух
И опыт, сын ошибок трудных,
И
Слайд 4Дата рождения:
Место рождения:
замок Мерчистон, в те годы предместье Эдинбурга
Дата смерти:
4 апреля 1617
Научная сфера:
математика
Известен как:
изобретатель
логарифмов
Джон Непер
John Napier
Слайд 7Вариант 2
-2; -1; 0; 1; 2; 4; 3; нет решения
Вариант
2; 1; 0; -1; -2; -3; нет решения
Задание 4. Вычислите, если возможно.
Ответы.
Слайд 11Леонард Эйлер
нем. Leonhard Euler
Дата рождения:
4 (15) апреля 1707
Место рождения:
Базель, Швейцария
Дата смерти:
7
Место смерти:
Санкт-Петербург, Российская империя
Научная сфера:
Математика, механика, физика, астрономия
Современное определение показательной, логарифмической и тригонометрических функций — заслуга Леонарда Эйлера, так же как и их символика.
Слайд 121) D(f) – область определения функции.
2) Чётность или нечётность функции.
4) Ограниченность
5) Наибольшие, наименьшие значения функции.
6) Непрерывность функции.
7) E(f) – область значений функции.
3) Промежутки возрастания, убывания функции.
План прочтения графика:
Слайд 15x
y
0
1
2
3
1
2
4
8
- 1
- 2
График функции y = loga x.
Опишите свойства
логарифмической
1 вариант:
при a > 1
2 вариант:
при 0 < a < 1
Слайд 16
1) D(f) = (0, + ∞);
2) не является ни чётной,
ни
3) возрастает на (0, + ∞);
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
Слайд 17
1) D(f) = (0, + ∞);
2) не является ни чётной,
ни
3) убывает на (0, + ∞);
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
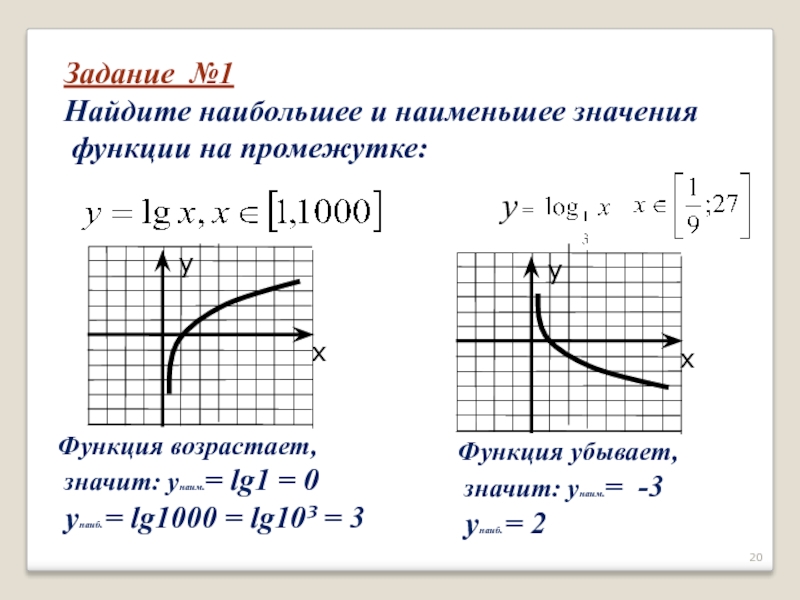
Слайд 20Задание №1
Найдите наибольшее и наименьшее значения
функции на промежутке:
Функция возрастает,
значит:
yнаиб. = lg1000 = lg10³ = 3
Функция убывает,
значит: yнаим.= -3
yнаиб. = 2
,
у =
Слайд 24Область определения логарифмической функции – вся
числовая прямая, а область значений
промежуток (0, + ∞).
Монотонность логарифмической функции зависит от
основания логарифма.
Не каждый график логарифмической функции проходит
через точку с координатами (1;0).
Слайд 25Логарифмическая функция не является ни чётной, ни
нечётной.
Логарифмическая функция имеет наибольшее
и не имеет наименьшего значения при a >1 и наоборот
при 0 < a < 1.
Проверка:
нет, да, нет, да, нет
Слайд 26Гл.VII,§ 4
№74,
82, 83 по группам
Дополнительно:
с помощью Интернет-ресурсов найти
области применения логарифмической функции.