- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему История возникновения логарифмов
Содержание
- 1. История возникновения логарифмов
- 2. Термин «логарифм» возник из сочетания греческих слов
- 3. Непер Джон (1550 – 1617), шотландский математик,
- 4. Безграничны приложения показательной и логарифмической функций в
- 5. Логарифмическая линейка (счётная линейка), счётный инструмент для
- 6. Еще недавно трудно было представить инженера без
- 7. …Даже изящные искусства питаются ею.Разве музыкальная гамма
- 8. Были поэты, которые не посвящали од эксоненте
- 9. Музыканты редко увлекаются математикой; большинство из них
- 10. Известный физик Эйхенвальд вспоминал «Товарищ мой по
- 11. Представьте же себе как неприятно был поражен
- 12. Логарифмическая спираль это плоская кривая, описываемая точкой,
- 13. Раковины морских животных могут расти лишь в
- 14. Слайд 14
- 15. Можно сказать, что эта спираль является математическим
- 16. Один из наиболее распространённых пауков, эпейра, сплетая
Термин «логарифм» возник из сочетания греческих слов logos – отношение, соотношение и arithmos – число и дословно переводится как отношение чисел. Логарифмы открыл шотландский математик Джон Непер в начале 17 века.
Слайд 2 Термин «логарифм» возник из сочетания греческих слов logos – отношение, соотношение
и arithmos – число и дословно переводится как отношение чисел.
Логарифмы открыл шотландский математик Джон Непер в начале 17 века.
Логарифмы открыл шотландский математик Джон Непер в начале 17 века.
Слайд 3 Непер Джон (1550 – 1617), шотландский математик, изобретатель логарифмов.
Непер является
так же составителем первой таблицы логарифмов, которая облегчила работу вычислителей многих поколений. Открытие логарифмов оказало большое влияние на развитие приложений математики.
Слайд 4 Безграничны приложения показательной и логарифмической функций в самых разнообразных областях науки
и техники, а ведь придумали логарифмы для облегчения вычислений. Более трёх столетий прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. Они помогали астрономам и инженерам, сокращая время на вычисления, и тем самым, как сказал знаменитый французский астроном, математик и физик Лаплас «Изобретение логарифмов, сократив работу астронома, продлило ему жизнь».
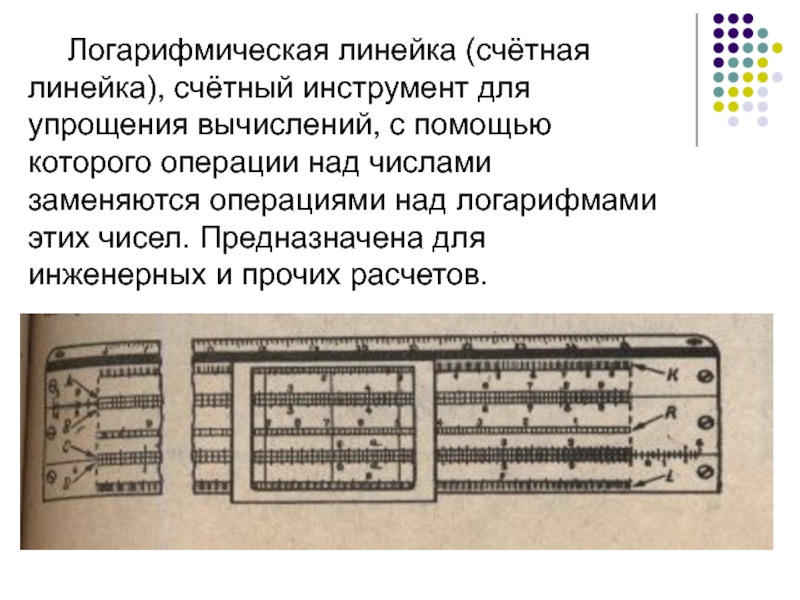
Слайд 5 Логарифмическая линейка (счётная линейка), счётный инструмент для упрощения вычислений, с помощью
которого операции над числами заменяются операциями над логарифмами этих чисел. Предназначена для инженерных и прочих расчетов.
Слайд 6 Еще недавно трудно было представить инженера без логарифмической линейки в кармане;
которая была изобретена через десять лет после появления логарифмов. Её изобрёл английским математик Гунтер. Она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь её из инженерного обихода вытиснили микрокалькуляторы. Но без логарифмической линейки не были бы построены ни первые компьютеры, ни микрокалькуляторы.
Слайд 7…Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых
логарифмов?
Из «Оды экспоненте»
Из «Оды экспоненте»
Многообразные применения показательной функции вдохновили английского поэта Элмера Брила и он написал «Оду экспоненте»
Мы знаем, что показательная и логарифмическая функции являются взаимно обратными. Показательную функцию так же называют экспонентой.
Логарифмы в искусстве
Слайд 8 Были поэты, которые не посвящали од эксоненте и логарифмам, но упоминали
их в своих стихах. Например в своём стихотворении поэт Борис Слуцкий написал строки
Потому – то слово пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы
Борис Слуцкий
Потому – то слово пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы
Борис Слуцкий
Слайд 9 Музыканты редко увлекаются математикой; большинство из них питают к этой науке
чувство уважения. Между тем, музыканты встречаются с математикой гораздо чаще, чем сами подозревают, и притом с такими «страшными» вещами, как логарифмы.
Слайд 10 Известный физик Эйхенвальд вспоминал «Товарищ мой по гимназии любил играть на
рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика не имеют друг с другом ничего общего. «Правда Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприемлемой».
Слайд 11 Представьте же себе как неприятно был поражен мой товарищ, когда я
доказал ему, что играя по клавишам своего рояля, он играет, собственно говоря, на логарифмах…»
И действительно, ступени 12-ти звуковой гаммы частот звуковых колебаний представляют собой логарифмы, основания которых равны двум.
И действительно, ступени 12-ти звуковой гаммы частот звуковых колебаний представляют собой логарифмы, основания которых равны двум.
Слайд 12Логарифмическая спираль это плоская кривая, описываемая точкой, движущейся по прямой, которая
вращается около одной из своих точек О (полюса логарифмической спирали) так, что логарифм расстояния движущейся точки от полюса изменяется пропорционально углу поворота; логарифмическая спираль пересекает под постоянным углом все прямые, выходящие из полюса.
Слайд 13 Раковины морских животных могут расти лишь в одном направлении. Чтобы не
слишком вытягиваться в длину, им приходится скручиваться, причём каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали. По этому раковины многих моллюсков, улиток, а так же рога таких млекопитающих как архары, (горные козлы), закручены по логарифмической спирали.
Слайд 15 Можно сказать, что эта спираль является математическим символом соотношения формы роста.
Великий немецкий поэт Иоганн Вольфганг Гёте считал её даже математическим символом жизни и духовного развития.
Очертания выраженные логарифмической спиралью имеют не только раковины. В подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.
Очертания выраженные логарифмической спиралью имеют не только раковины. В подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.
Слайд 16 Один из наиболее распространённых пауков, эпейра, сплетая паутину, закручивает нити вокруг
центра по логарифмической спирали.
По логарифмическим спиралям закручены и многие галактики, в частности галактика, которой принадлежит Солнечная система.
По логарифмическим спиралям закручены и многие галактики, в частности галактика, которой принадлежит Солнечная система.