- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Факультативное занятие. Комбинаторные задачи
Содержание
- 1. Факультативное занятие. Комбинаторные задачи
- 2. ЗадачиОтработать умения решать простейшие комбинаторные задачиПодготовиться к
- 3. ЭтапыЧто такое комбинаторика?Элементарные сведенияРешение задач 1 части Приобретение навыков решения задач 2 частиПолезные ссылки
- 4. Число, положение и комбинация -три взаимно пересекающиеся,но
- 5. КОМБИНАТОРИКА – область математики, в которой изучаются
- 6. КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления перебора
- 7. Устный счетВычислите факториал1! и 3! Вспомните формулу перестановок и вычислитеР2 и Р4 3! = 1۰2۰3=6Р4 = 4!=1۰2۰3۰4=24
- 8. Вспомните формулу размещений и вычислитеВспомните формулу перестановок и вычислите
- 9. Ответьте на вопросы тестаПри выборе подходящего комплекта
- 10. 3. Подсчитывая число маршрутов следования из пункта
- 11. 5! – это: А.сумма чисел от 1
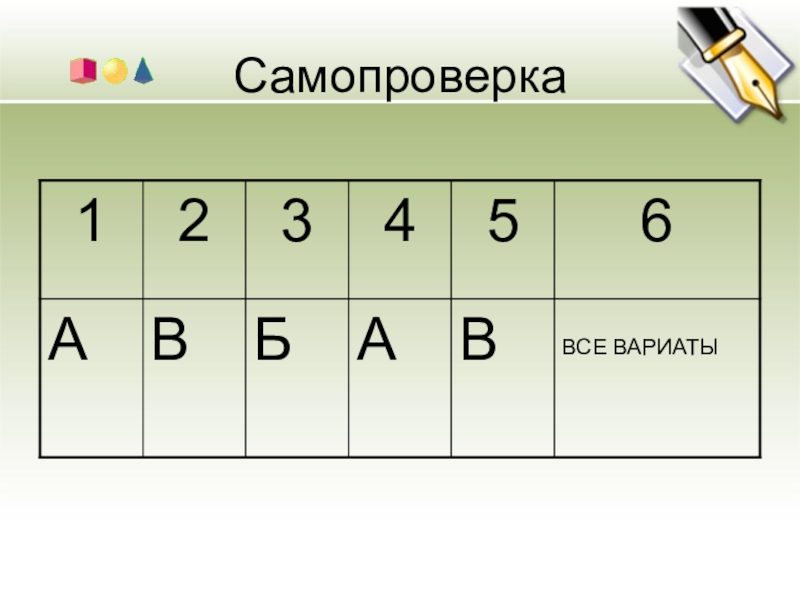
- 12. Самопроверка
- 13. Задания 1 части Выписаны все трехзначные числа
- 14. 5. В конференции участвовали 30 человек. Каждый
- 15. Задания 2 части1.(2) При встрече 5 человек
- 16. 1) Сколько диагоналей в выпуклом десятиугольнике?
- 17. Подведём итоги…
- 18. Приложения
- 19. ШпаргалкаПусть требуется выполнить одно за другим k
- 20. Комбинаторика является древнейшей и, возможно, ключевой ветвью
- 21. Термин "комбинаторика"
- 22. Так, Леонард Эйлер рассматривал задачи о разбиении
- 23. 1. Самый младший разряд числа 426-единицы, их
- 24. 2. Применим правило умножения (и)
- 25. 3. Урок математики можно поставить любым из
- 26. 6 способов4. Проще и быстрее выписать все
- 27. 5. Каждый их 30 участников конференции раздал по 29 визитных карточек. Всего 29∙30=870 карточек.возврат
- 28. 6. На первое место можно поставить любую
- 29. 7. На первое место можно поставить любую
- 30. 1. Каждое рукопожатие – пара, которую составляем
- 31. 2. Нечетных цифр пять:1;3;5;7;9.Однозначных- 5 чисел.По правилу умноженияДвузначных - 5∙5=25Трехзначных – 125, четырехзначных - 625Всего 5+25+125+625=780.возврат55
- 32. возврат3. Биология однозначно определена, её не учитываем.Для
- 33. 4. Пусть в 1 команде N игроков2
- 34. Литература, полезные ссылки Айгнер
Слайд 1Еще Конфуций сказал: "Три пути ведут к знанию. Путь размышлений -
Слайд 2Задачи
Отработать умения решать простейшие комбинаторные задачи
Подготовиться к решению комбинаторных задач на
Расширить математический кругозор
Шпаргалка и немного истории
Слайд 3Этапы
Что такое комбинаторика?
Элементарные сведения
Решение задач 1 части
Приобретение навыков решения задач
Полезные ссылки
Слайд 4Число, положение и комбинация -
три взаимно пересекающиеся,
но различные сферы мысли,
к которым
все математические идеи.
Английский математик Джеймс Джозеф Сильвестр (1814-1897)
Слайд 5КОМБИНАТОРИКА – область математики, в которой изучаются вопросы о том, сколько
Слайд 6КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления перебора всех возможных вариантов или
ОРГАНИЗОВАННЫЙ ПЕРЕБОР –
строгий порядок разбора всех случаев,
возможных решений.
Слайд 7Устный счет
Вычислите факториал
1! и 3!
Вспомните формулу перестановок и вычислите
Р2 и Р4
3! = 1۰2۰3=6
Р4 = 4!=1۰2۰3۰4=24
Слайд 9Ответьте на вопросы теста
При выборе подходящего комплекта одежды мы пользуемся:
А.сочетанием,
Б.перебором,
В.пересечением множеств.
2. Комбинаторика изучает:
А.деятельность комбинатов бытового обслуживания,
Б.способы пошива комбинезонов,
В.способы решения задач на различные комбинации объектов.
Слайд 103. Подсчитывая число маршрутов следования из пункта А в пункт В
А.сложения,
Б.умножения,
В.возведения в степень.
4. Для вычисления количества всевозможных пар вашей группы необходимо знать формулы:
А.сочетаний,
Б.сокращенного умножения,
В.теорему Пифагора.
Ответьте на вопросы теста
Слайд 115! – это:
А.сумма чисел от 1 до 5,
Б.квадрат числа
В.произведение натуральных чисел от 1 до 5 (вычислите).
6. Комбинаторные задачи встречаются в профессиональной деятельности:
А. парикмахера-визажиста,
Б. диспетчера автовокзала,
В. завуча школы,
Г. экономиста,
Д. повара
(добавьте свой пример)
Ответьте на вопросы теста
Слайд 13Задания 1 части
Выписаны все трехзначные числа из цифр
0, 2,
2. В классе 15 девочек и 10 мальчиков. Сколькими способами можно выбрать для дежурства двоих: 1 девочку и 1 мальчика?
3. В расписании на среду 4 урока: математика, русский и 2 урока физкультуры. Сколькими способами можно составить расписание?
4. В коробке 4 шара: белый, синий, красный, зеленый. Из неё извлекают 2 шара Сколько различных комбинаций можно получить? Сколько вариантов вынуть 2 шара различного цвета?
Слайд 145. В конференции участвовали 30 человек. Каждый обменялся визиткой. Сколько всего
6. Сколько трехзначных чисел можно записать, используя цифры 0, 2, 4, 6?
7. В чемпионате по футболу играет 10 команд. Сколькими способами могут распределиться три призовых места?
Слайд 15Задания 2 части
1.(2) При встрече 5 человек обменялись рукопожатиями. Сколько сделано
2.(4) Из нечетных цифр составляют все возможные числа, содержащие не более 4 цифр. Сколько существует таких чисел?
3.(4) Сколькими способами можно составить расписание на день , если должно быть 5 уроков: алгебра, геометрия, физика, биология, география, при этом алгебра и геометрия должны стоять рядом, а урок биологии обязательно первым?
4.(6) После матча каждый игрок одной команды обменялся рукопожатием с каждым игроком другой. Сколько игроков было всего на площадке, если рукопожатий было совершено 323?
Слайд 161) Сколько диагоналей в выпуклом десятиугольнике?
2) Встретились несколько друзей
3) Придумайте как можно больше комбинаторных задач с использованием данных объектов: Четверо друзей: Катя, Олег, Света, Андрей.
Закрепление материала
Слайд 19Шпаргалка
Пусть требуется выполнить одно за другим k действий. Если первое действие
n! = 1×2 ×… ×n
Комбинации из n-элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются перестановками из n элементов Р = n!
Комбинации из n элементов по k , отличающиеся друг от друга лишь составом элементов, называются сочетаниями из n элементов по k. Количество сочетаний можно посчитать по формуле
Комбинации из n элементов по k, отличающиеся друг от друга либо
составом элементов, либо порядком их расположения, называются
размещениями из n элементов по k (k≤n).
Слайд 20 Комбинаторика является древнейшей и, возможно, ключевой ветвью математики. В математике есть
Немного истории
Слайд 21 Термин "комбинаторика" был введён в математический
Г.В. Лейбниц
Слайд 22Так, Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о
возврат
Л. Эйлер
Я. Бернулли
Слайд 231. Самый младший разряд числа 426-единицы, их 6, увеличить нельзя. Можно
возврат
4
2
6
0
4
Слайд 242. Применим правило умножения (и) 1 девочку можно
возврат
Слайд 253. Урок математики можно поставить любым из 4 уроков, затем русский
По правилу умножения 4∙3=12
возврат
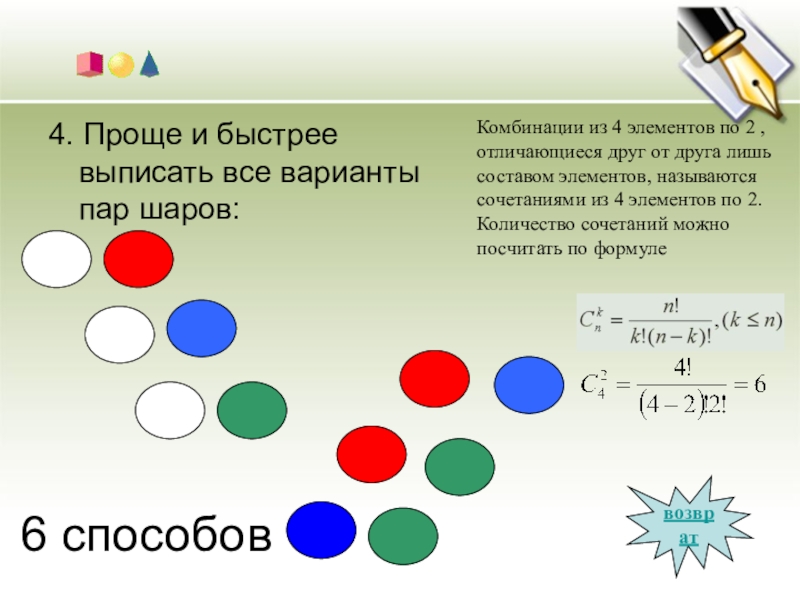
Слайд 266 способов
4. Проще и быстрее выписать все варианты пар шаров:
возврат
Комбинации из
Слайд 275. Каждый их 30 участников конференции раздал по 29 визитных карточек.
возврат
Слайд 286. На первое место можно поставить любую цифру, кроме 0 –
3∙4 ∙4=48.
возврат
Слайд 297. На первое место можно поставить любую из 10 команд, на
возврат
Комбинации из 10 элементов по 3 , отличающиеся друг от друга либо составом элементов, либо порядком их расположения называются размещениями из 10 элементов по 3. Количество размещений можно посчитать по формуле
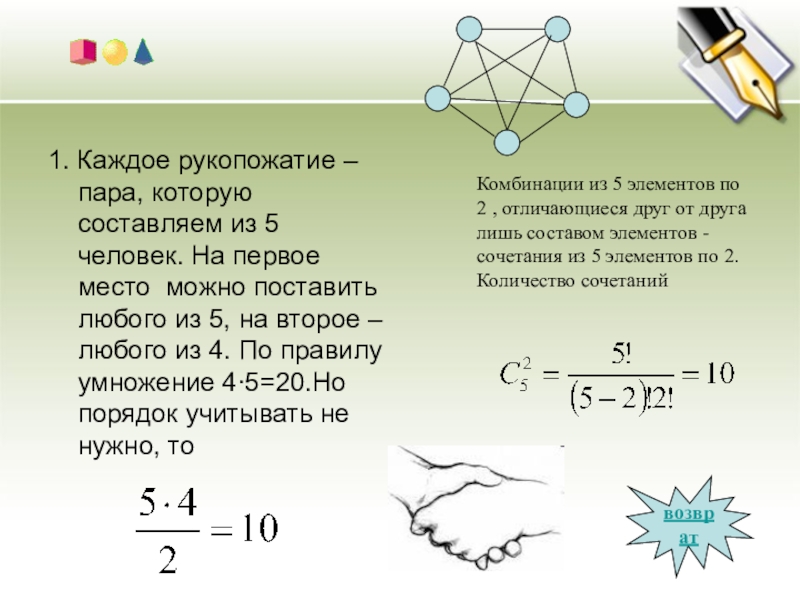
Слайд 301. Каждое рукопожатие – пара, которую составляем из 5 человек. На
возврат
Комбинации из 5 элементов по 2 , отличающиеся друг от друга лишь составом элементов -сочетания из 5 элементов по 2. Количество сочетаний
Слайд 312. Нечетных цифр пять:1;3;5;7;9.
Однозначных- 5 чисел.
По правилу умножения
Двузначных - 5∙5=25
Трехзначных –
Всего 5+25+125+625=780.
возврат
5
5
Слайд 32
возврат
3. Биология однозначно определена, её не учитываем.
Для совместных уроков алгебры и
3 варианта расположения в расписании, при этом в
2-х комбинациях(алгебра-геометрия, геометрия-алгебра).
Физику на любое место из двух оставшихся,
географию на последнее оставшееся.
По правилу
умножения 3∙2∙2 1=12.
Ответ: 12.
Слайд 334. Пусть в
1 команде N игроков
2 команде M игроков. N
было совершено N⋅M рукопожатий. Т.е. N⋅M=323- уравнение в целых числах. Варианты разложения на два множителя :
1⋅323=323 и 17⋅19=323
То значения N=1; 17; 19.
В хоккейной команде не может быть 1 человек.
Следовательно в командах по 17 и 19 человек соответственно, их сумма 17+19=36.
Ответ: 36 человек
возврат