- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Дифференциальное исчисление функций одной переменной
Содержание
- 1. Дифференциальное исчисление функций одной переменной
- 2. ВОПРОС 1Определение производной функции, её геометрический и механический смысл.
- 3. №1. Задача о прямолинейном движении материальной точки
- 4. №1. Задача о прямолинейном движении материальной точки
- 5. №1. Задача о прямолинейном движении материальной точки
- 6. Дана кривая L, а на ней отмечена
- 7. №2. Задача о касательной к кривой Угловой
- 8. – если Q(t) – количество электричества, проходящее
- 9. Производная функции
- 10. Для нахождения производной функции y=f(x) нужно:Аргументу x0
- 11. Примеры 1. Найти производную функции y = c.
- 12. Физический смысл производной: Геометрический смысл производной: Если функция y=f(x)
- 13. Уравнение касательной: Уравнение нормали: Если
- 14. 1) найдём значение функции в точке x0:
- 15. ВОПРОС 2Производные основных элементарных функций.
- 16. Таблица производных: 1.2.3.4.5.6.7.
- 17. Таблица производных: 8. Производные тригонометрических функций:9. Производные обратных тригонометрических функций:
- 18. ВОПРОС 3Правила нахождения производных.
- 19. Теорема 1. Производная суммы (разности) двух функций сумме (разности) производных этих функций:Пример:
- 20. Теорема 2. Производная произведения
- 21. Теорема 3. Производная частного
- 22. Теорема 4. Если функция
- 23. Теорема 5. Если функция
- 24. СПАСИБОЗАВНИМАНИЕ!
Слайд 3№1. Задача о прямолинейном движении материальной точки
Пусть материальная точка движется
Каждому значению времени t соответствует определенное расстояние S, пройденное точкой от начала отсчета O за время t .
Значит, S(t) – функция времени, описывающая закон движения.
Слайд 4№1. Задача о прямолинейном движении материальной точки
Пусть в момент времени
А в момент времени t = t0 + t – расстояние S(t).
Тогда за время t точка прошла расстояние:
Слайд 5№1. Задача о прямолинейном движении материальной точки
Мгновенная скорость движения:
Средняя скорость
Чем меньше t, тем точнее средняя скорость выражает скорость движения в момент времени t.
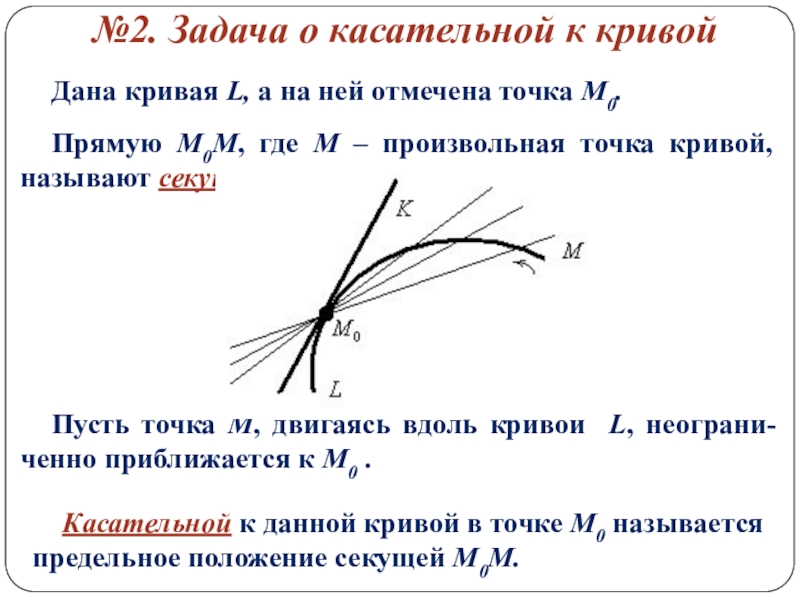
Слайд 6Дана кривая L, а на ней отмечена точка М0.
Прямую М0М, где
Пусть точка М, двигаясь вдоль кривой L, неограни-ченно приближается к М0 .
№2. Задача о касательной к кривой
Касательной к данной кривой в точке М0 называется предельное положение секущей М0М.
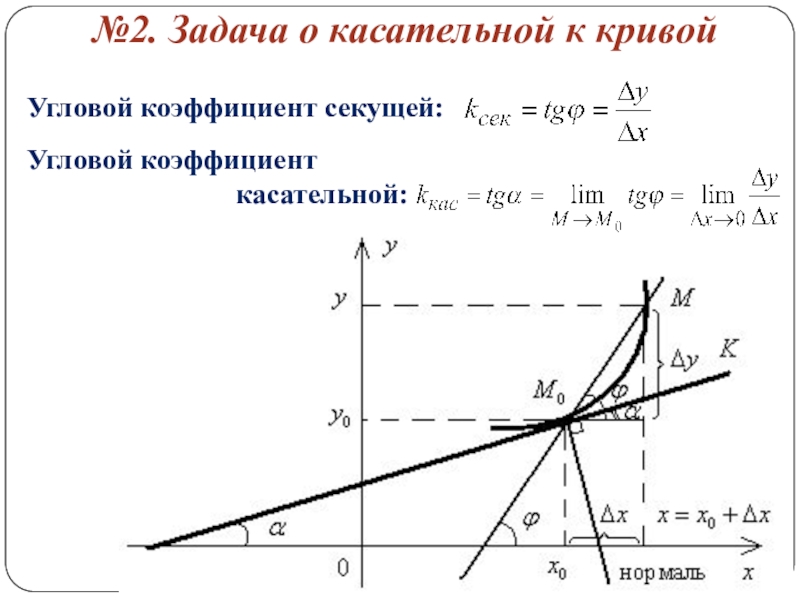
Слайд 7№2. Задача о касательной к кривой
Угловой коэффициент секущей:
Угловой коэффициент
Слайд 8– если Q(t) – количество электричества, проходящее через поперечное сечение проводника
– если N(t) – количество вещества, вступающего в химическую реакцию за время t, то скорость химической реакции в момент времени t:
– если m(t) – масса неоднородного стержня между точками, то линейная плотность стержня в точке x:
№3. Аналогичные задачи
То есть везде требуется найти предел отношения приращения функции к приращению аргумента.
Слайд 10Для нахождения производной функции y=f(x) нужно:
Аргументу x0 задать приращение x:
Найти
Составить отношение приращения функции к приращению аргумента
Найти предел этого отношения при x 0:
Слайд 11Примеры
1. Найти производную функции y = c.
Зададим x0 приращение х:
Найдём приращение функции f(x0)=c и f(x)=c
Вычислим производную:
2. Найти производную функции y = х.
Зададим x0 приращение х: х=x – x0
Найдём приращение функции f(x0)=x0 и f(x)=x0+х
Вычислим производную:
Слайд 12Физический смысл производной:
Геометрический смысл производной:
Если функция y=f(x) описывает какой-либо физический
Производная y’ в точке x0 равна угловому коэффи-циенту касательной к графику функции y=f(x) в точке с абсциссой x0.
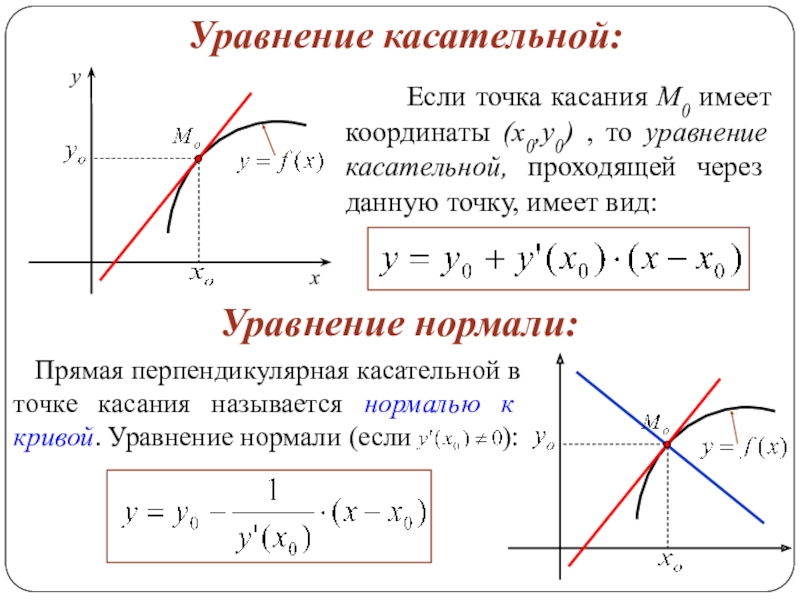
Слайд 13Уравнение касательной:
Уравнение нормали:
Если точка касания М0 имеет
Прямая перпендикулярная касательной в точке касания называется нормалью к кривой. Уравнение нормали (если ):
х
у
Слайд 141) найдём значение функции в точке x0:
y(x0) = 23 =
2) найдём производную функции:
y’ = 3x2;
3) найдём значение производной в точке x0:
y’ (x0) = 322=12.
уравнение касательной:
y=8+12(x – 2).
5) уравнение нормали:
y=8 – (x – 2).
Пример
Составить уравнение касательной и нормали к кривой y=x3 в точке с абсциссой x0=2.
Слайд 17Таблица производных:
8. Производные тригонометрических функций:
9. Производные обратных тригонометрических функций:
Слайд 19Теорема 1.
Производная суммы (разности) двух функций сумме
Пример:
Слайд 20Теорема 2.
Производная произведения двух функций равна произведению
Следствия: 1.
2.
Пример:
Слайд 21Теорема 3.
Производная частного двух функций
Пример:
Слайд 22Теорема 4.
Если функция u=(x) имеет производную u’x
т.е. производная внешней функции (по промежуточному аргументу u) умножается на производную внутренней функции (по независимому аргументу x).
Пример:
Слайд 23Теорема 5.
Если функция y=f(x) строго монотонна на
Пусть , обратная функция .
Пример: