2
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Демонстрационный материал для 9 класса по теме Квадратичная функция.
Содержание
- 1. Демонстрационный материал для 9 класса по теме Квадратичная функция.
- 2. Презентация по алгебре учителя математики МКОУ СОШ
- 3. Определение квадратичной функции- квадратичная функция а,b,c –
- 4. ХУ011ху = х2У =2х2 у =
- 5. ХУ011у =½х2у = х2у = 2х2у =
- 6. ХУ011у =½х2у = х2у = 2х2у =
- 7. ХУ011-2-10 1410 14632361-2-3-2 1
- 8. ХУ011 х у = х2x у=(х
- 9. ХУ011
- 10. ХУ011
- 11. Построение графика квадратичной функции
- 12. Построение графика квадратичной функции у = ах2
- 13. Примеры построения графиков квадратичной функцииху101Пример 1: построить
- 14. Примеры построения графиков квадратичной функцииху101Пример 2: построить
- 15. Примеры построения графиков квадратичной функцииху101Пример 3: построить
Слайд 2Презентация по алгебре учителя математики МКОУ СОШ №1 пгт. Палана Камчатский край Учебник алгебры 9 класс. Авторы:
Слайд 3Определение квадратичной функции
- квадратичная функция
а,b,c – некоторые числа, где
а ≠
х – независимая переменная
у = аx+b - линейная функция
Слайд 4Х
У
0
1
1
х
у = х2
У =2х2
у = ½х2
у =-½х2
-2
-1
0
1
3
4
1
0
1
4
9
8
2
0
2
8
18
2
0,5
0
0,5
2
4,5
-2
-0,5
0
-0,5
-2
-4,5
Графики функции у = ах2
Функция у = ах2 является частным случаем квадратичной функции у = ах2 + bх + с, где b = 0,с = 0.
у = х2
у = 2х2
у = ½ х2
у = -½ х2
Слайд 5Х
У
0
1
1
у =½х2
у = х2
у = 2х2
у = -½х2
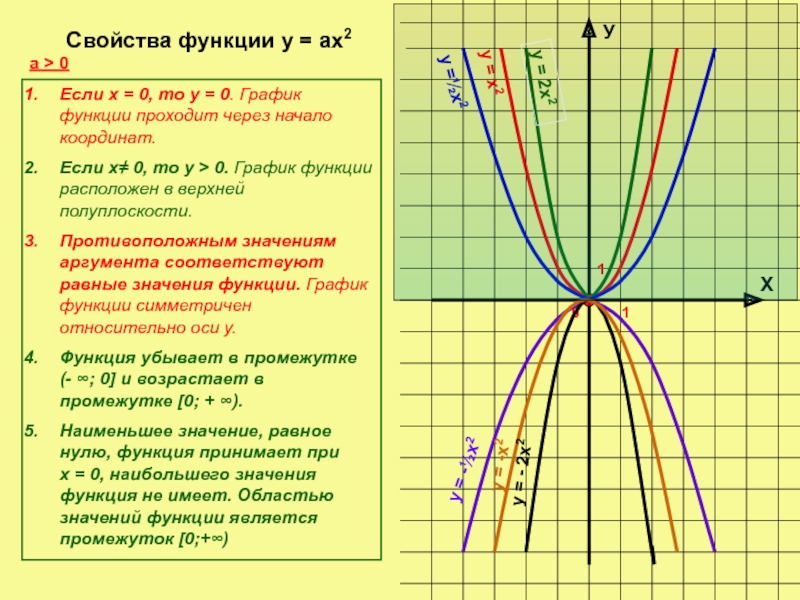
Свойства
а > 0
Если х = 0, то у = 0. График функции проходит через начало координат.
Если х≠ 0, то у > 0. График функции расположен в верхней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
Функция убывает в промежутке (- ∞; 0] и возрастает в промежутке [0; + ∞).
Наименьшее значение, равное нулю, функция принимает при х = 0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+∞)
у = -х2
у = - 2х2
Слайд 6Х
У
0
1
1
у =½х2
у = х2
у = 2х2
у = -½х2
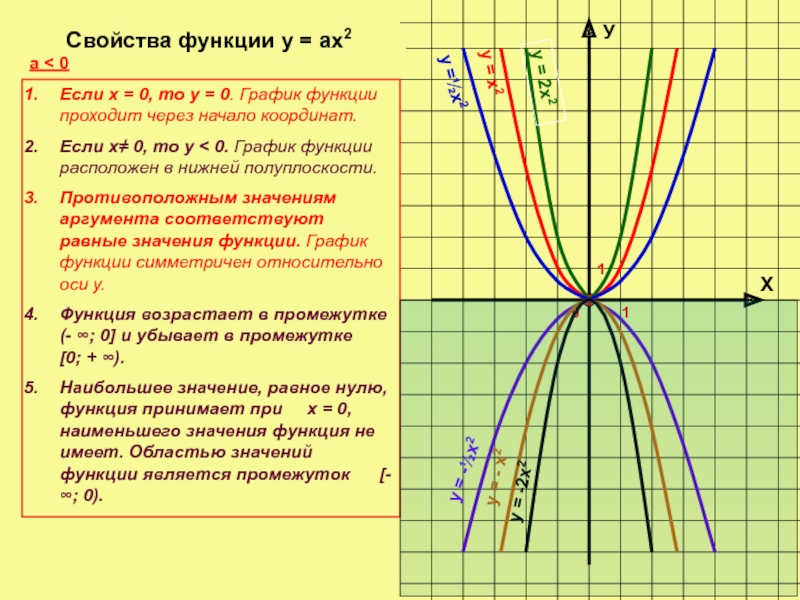
Свойства
а < 0
Если х = 0, то у = 0. График функции проходит через начало координат.
Если х≠ 0, то у < 0. График функции расположен в нижней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
Функция возрастает в промежутке (- ∞; 0] и убывает в промежутке [0; + ∞).
Наибольшее значение, равное нулю, функция принимает при х = 0, наименьшего значения функция не имеет. Областью значений функции является промежуток [- ∞; 0).
у = - х2
у = -2х2
Слайд 7Х
У
0
1
1
-2
-1
0
1
4
1
0
1
4
6
3
2
3
6
1
-2
-3
-2
1
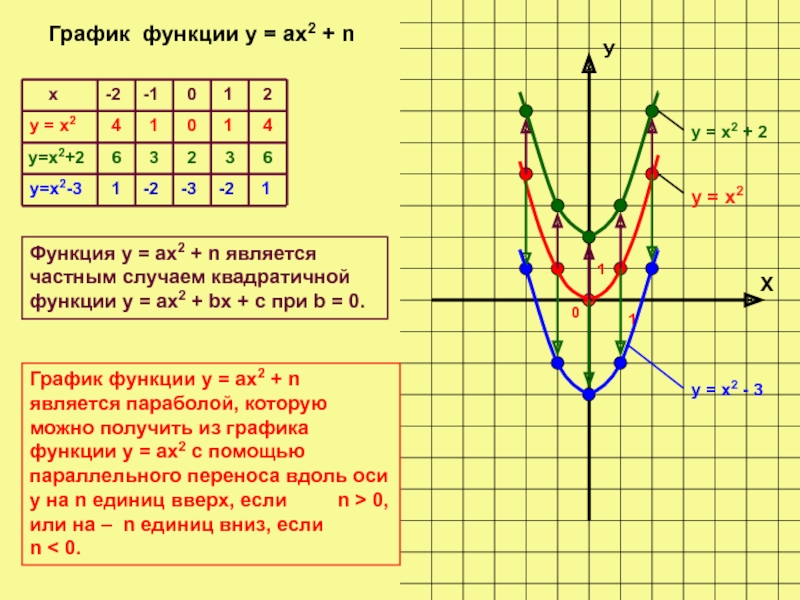
График функции у = ах2 + n
у = х2
у = х2 + 2
у = х2 - 3
График функции у = ах2 + n является параболой, которую можно получить из графика функции у = ах2 с помощью параллельного переноса вдоль оси у на n единиц вверх, если n > 0, или на – n единиц вниз, если n < 0.
х
2
у = х2
у=х2+2
у=х2-3
Функция у = ах2 + n является частным случаем квадратичной функции у = ах2 + bх + с при b = 0.
Слайд 8Х
У
0
1
1
х
у = х2
x
у=(х - 2)2
-2
-1
0
1
2
4
1
0
4
0
1
2
3
4
4
1
0
1
4
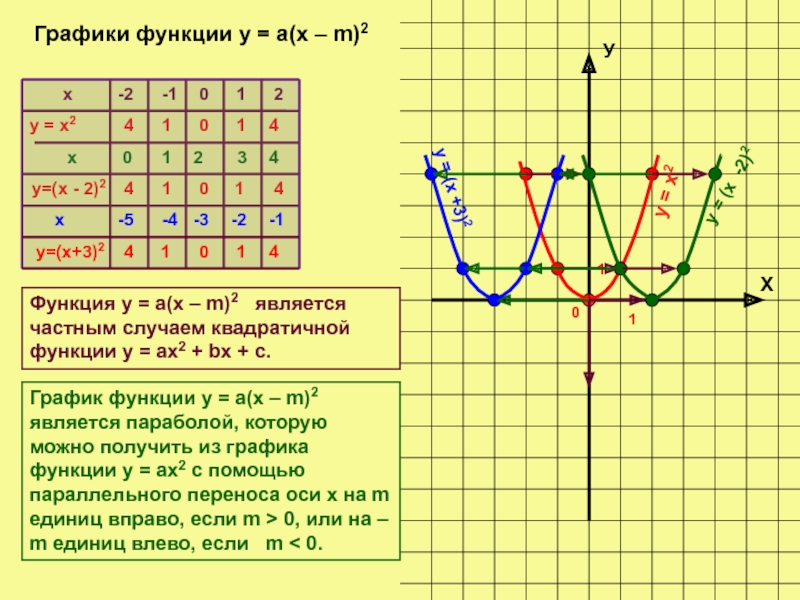
Графики функции у = а(х – m)2
у = х2
у = (х -2)2
у = (х +3)2
Функция у = а(х – m)2 является частным случаем квадратичной функции у = ах2 + bx + c.
График функции у = а(х – m)2 является параболой, которую можно получить из графика функции у = ах2 с помощью параллельного переноса оси х на m единиц вправо, если m > 0, или на – m единиц влево, если m < 0.
х
у=(х+3)2
-5
-4
-3
-2
-1
4
1
0
1
4
Слайд 9Х
У
0
1
1
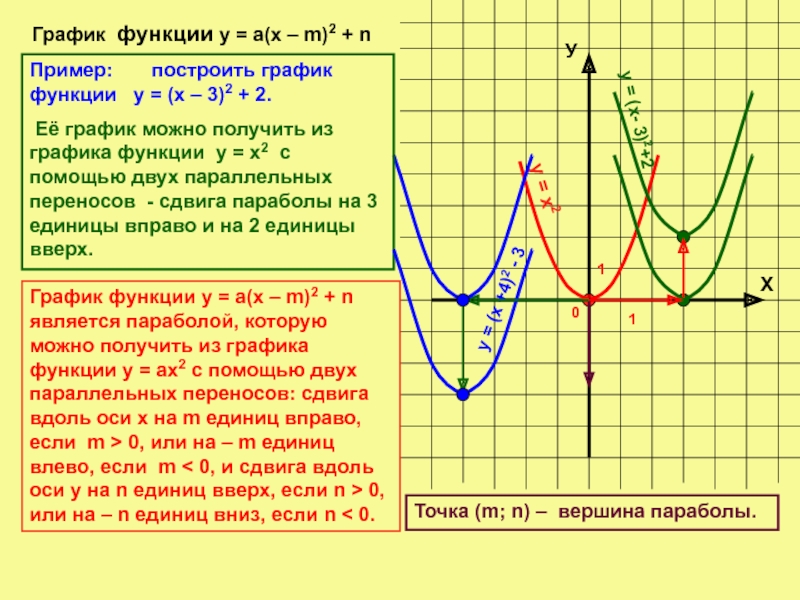
График функции у = а(х – m)2 + n
у = х2
у = (х- 3)2+2
у = (х +4)2 - 3
График функции у = а(х – m)2 + n является параболой, которую можно получить из графика функции у = ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m > 0, или на – m единиц влево, если m < 0, и сдвига вдоль оси у на n единиц вверх, если n > 0, или на – n единиц вниз, если n < 0.
Пример: построить график функции у = (х – 3)2 + 2.
Её график можно получить из графика функции у = х2 с помощью двух параллельных переносов - сдвига параболы на 3 единицы вправо и на 2 единицы вверх.
Точка (m; n) – вершина параболы.
Слайд 10Х
У
0
1
1
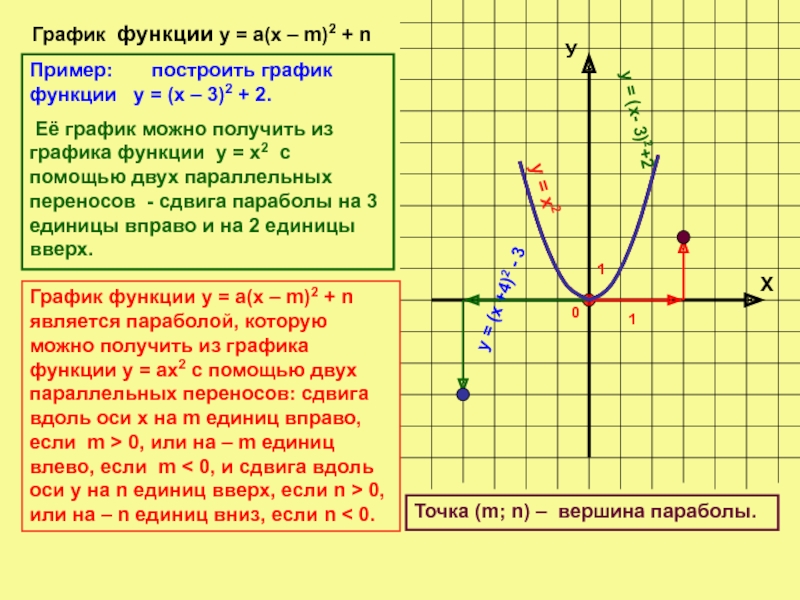
График функции у = а(х – m)2 + n
у = х2
у = (х- 3)2+2
у = (х +4)2 - 3
График функции у = а(х – m)2 + n является параболой, которую можно получить из графика функции у = ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m > 0, или на – m единиц влево, если m < 0, и сдвига вдоль оси у на n единиц вверх, если n > 0, или на – n единиц вниз, если n < 0.
Пример: построить график функции у = (х – 3)2 + 2.
Её график можно получить из графика функции у = х2 с помощью двух параллельных переносов - сдвига параболы на 3 единицы вправо и на 2 единицы вверх.
Точка (m; n) – вершина параболы.
Слайд 11Построение графика квадратичной функции
Представим формулу, которой задана квадратичная функция у = ах2 + bх + с в виде у = а(х – m)2 + n.
Графиком функции у=ах2+bх+ с является парабола, вершиной которой является точка (m;n). Осью симметрии служит прямая х = m, параллельная оси у. При а>0 ветви параболы направлены вверх, а при а<0 – вниз.
Слайд 12Построение графика квадратичной функции
у = ах2 + bx + c
Найти координаты вершины параболы и отметить её в координатной плоскости. Провести ось симметрии параболы.
Построить ещё несколько точек, принадлежащих параболе: составить таблицу значений функции для точек слева или справа от вершины.
Соединить отмеченные точки плавной линией, учитывая направление ветвей параболы.
Слайд 13Примеры построения графиков квадратичной функции
х
у
1
0
1
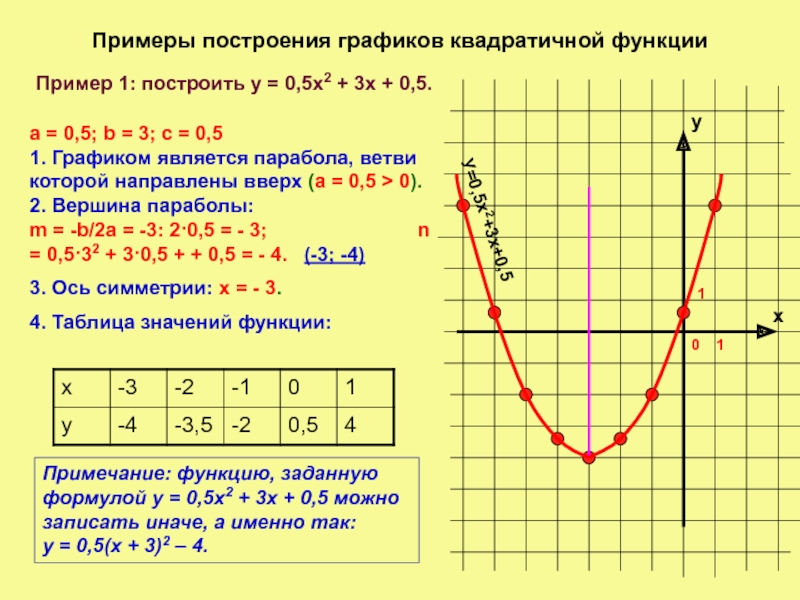
Пример 1: построить у = 0,5х2 +
a = 0,5; b = 3; c = 0,5 1. Графиком является парабола, ветви которой направлены вверх (а = 0,5 > 0). 2. Вершина параболы: m = -b/2а = -3: 2·0,5 = - 3; n = 0,5·32 + 3·0,5 + + 0,5 = - 4. (-3; -4)
3. Ось симметрии: х = - 3.
4. Таблица значений функции:
Примечание: функцию, заданную формулой у = 0,5х2 + 3х + 0,5 можно записать иначе, а именно так: у = 0,5(х + 3)2 – 4.
У=0,5х2+3х+0,5
Слайд 14Примеры построения графиков квадратичной функции
х
у
1
0
1
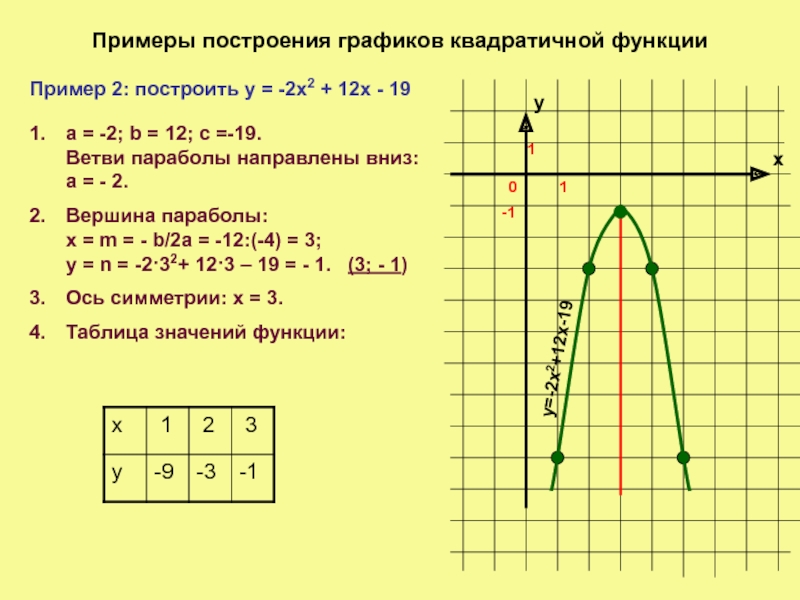
Пример 2: построить у = -2х2 +
a = -2; b = 12; c =-19. Ветви параболы направлены вниз: а = - 2.
Вершина параболы: х = m = - b/2а = -12:(-4) = 3; у = n = -2·32+ 12·3 – 19 = - 1. (3; - 1)
Ось симметрии: х = 3.
Таблица значений функции:
-1
у=-2х2+12х-19
Слайд 15Примеры построения графиков квадратичной функции
х
у
1
0
1
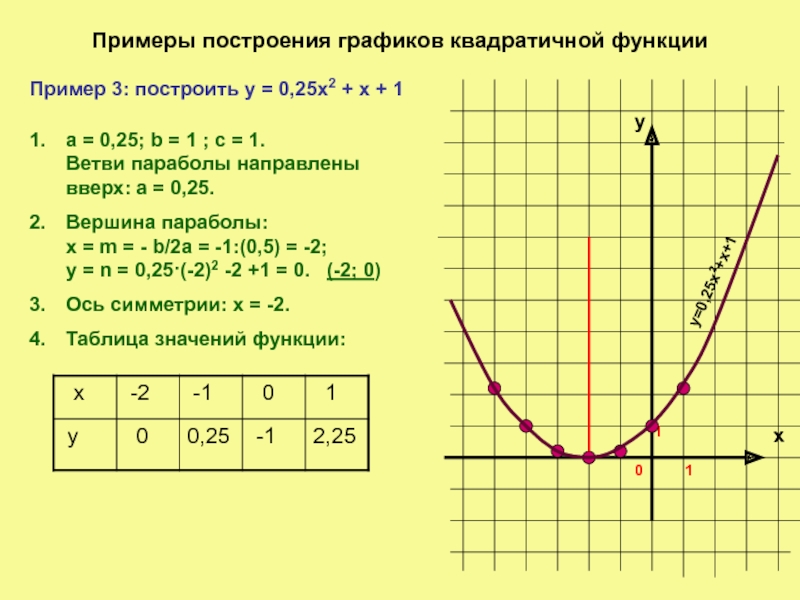
Пример 3: построить у = 0,25х2 +
a = 0,25; b = 1 ; c = 1. Ветви параболы направлены вверх: а = 0,25.
Вершина параболы: х = m = - b/2а = -1:(0,5) = -2; у = n = 0,25·(-2)2 -2 +1 = 0. (-2; 0)
Ось симметрии: х = -2.
Таблица значений функции:
у=0,25х2+х+1