- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Софизмы
Содержание
- 1. Софизмы
- 2. Математический софизм – удивительное утверждение, в доказательстве
- 3. Что
- 4. Виды софизмоварифметическиегеометрическиеалгебраическиелогические
- 5. Арифметический
- 6. Арифметический
- 7. « Дважды два - пять!»Сейчас мы вместе
- 8. Слайд 8
- 9. Слайд 9
- 10. Геометрический софизм «Катет равен гипотенузе»
- 11. «Спичка вдвое длиннее телеграфного столба!!!» Пусть а дм
- 12. Логический софизм Девушка –
- 13. А. Г.
Слайд 1Математические софизмы
Подготовила учитель математики
МБОУ СОШ с Красное имени Героя Советского
Мулярчук Светлана Михайловна
Слайд 2Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а
Мартин Гарднер
Слайд 3 Что такое софизм?
Софизм (от греч.
Софизм - формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положений (словарь Ожегова).
Слайд 5 Арифметический софизм
« Дважды два
Возьмем в качестве исходного соотношения следующее очевидное равенство:
4:4= 5:5 (1)
После вынесения за скобки общего множителя из каждой части равенства будем иметь:
4∙(1:1)=5∙(1:1) (2)
или
(2∙2)(1:1)=5(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем:
2∙2=5
Где ошибка?
.
Нельзя выносить множитель за скобки, как это сделано в равенстве (2).
Слайд 6 Арифметический софизм
«Два неодинаковых натуральных
Решим систему двух уравнений: х+2у=6, (1) у=4- х/2 (2) Сделаем это подстановкой у из 2го уравнения в 1, получаем х+8-х=6, откуда 8=6
Где ошибка?
Уравнение (2) можно записать как х+2у=8, так что исходная система запишется в виде: Х+2у=6, Х+2у=8. В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения.
Слайд 7« Дважды два - пять!»
Сейчас мы вместе с вами докажем, что
16 - 36 + 81/4 = 25 - 45 + 81/4 (2)
Преобразуем выражение: 4*4 - 2*4*9/2 + (9/2)*(9/2) = 5*5 - 2*5*9/2 + (9/2)*(9/2) (3)
Теперь можно заметить, что в левой и правой части выражения (3) записаны произведения вида: a 2 -2ab+b2 , то есть, квадрат разности: (a-b)2 . В нашем случае слева a=4, b=9/2, а справа a=5, b=9/2. Поэтому перепишем выражение (3) в виде квадратов разности: (4 - 9/2)2 = (5 - 9/2)2 .А следовательно, 4 - 9/2 = 5 - 9/2 10 И наконец, получаем долгожданное равенство: 4 = 5 или, если угодно: 2*2 = 5
Где ошибка?
В преобразования, разумеется, закралась ошибка. А именно, при переходе из (4) в (5) совсем забыли, что равенство квадратов вовсе не означает равенство значений, возведенных в квадрат: они могут быть противоположны друг другу, как в нашем случае: 4-9/2 равно -1/2, а 5-9/2 равно 1/2. А квадраты этих значений одинаковы
Слайд 8
Возьмем два произвольных неравных
а2 -2ab+b2 = b2 -2ab+ а2
Слева и справа стоят полные квадраты, т. е. можем записать
(а-b)2 = (b-а)2. (1)
Извлекая из обеих частей последнего равенства квадратный корень, получим:
a-b = b-a (2)
или 2а = 2b, или окончательно
a=b.
Где ошибка?
ОШИБКА В ПЕРЕХОДЕ ОТ РАВЕНСТВА (1) К РАВЕНСТВУ(2)
Алгебраический софизм
«Все числа равны между собой»
Слайд 9
Возьмем два положительных числа
Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны
«Отрицательное число больше положительного».
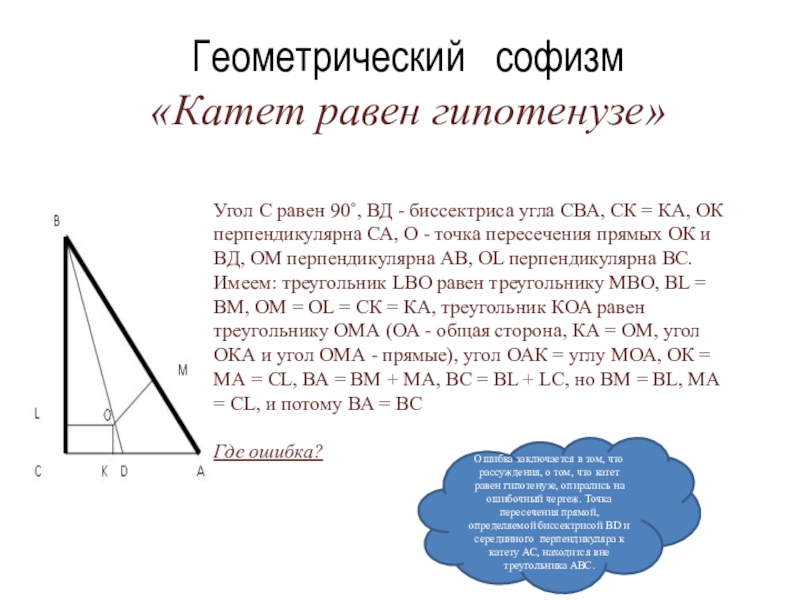
Слайд 10Геометрический софизм
«Катет равен гипотенузе»
. Где ошибк
Угол С равен
Где ошибка?
Ошибка заключается в том, что рассуждения, о том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне треугольника АВС.
Слайд 11«Спичка вдвое длиннее телеграфного столба!!!»
Пусть а дм –длина спички и b
Разность между b и a обозначим через c .
Имеем:
b - a = c, b = a + c.
Перемножаем два эти равенства по частям, находим:
b2 - ab = ca + c2.
Вычтем из обеих частей bc. Получим:
b2- ab - bc = ca + c2 – bc
или
b(b - a - c) = - c(b - a - c) (1)
Откуда:
b = - c, но c = b – a
Поэтому
b = a - b, или a = 2b.
Где ошибка???
В выражении
b(b-a-c )= -c(b-a-c)
производится деление
на (b-a-c),
а этого делать нельзя,
так как b-a-c=0.
Значит, спичка не может быть вдвое длиннее телеграфного столба!!!
Слайд 12 Логический софизм
Девушка – это человек. Девушка является
Где ошибка?
так как здесь наблюдается противоречие. (Данный софизм является доказательством от противного)
Слайд 13
А. Г. Мадера, Д. А. Мадера
Энциклопедический словарь юного математика.
Брадис В. М., Минковский В. Л., Харчева Л. К. «Ошибки в математических рассуждениях».
Перельман Я. И. «Занимательная математика».
Аменицкий Н. «Математические развлечения и любопытные приёмы мышления». М.,1912г.
Богомлов С. А. «Актуальная бесконечность.» М.; Л., 1934г.
Горячев Д. Н., Воронец А. Н. «Задачи, вопросы и софизмы для любителей математики», М., 1903.
Лямин А. А. «Математические парадоксы и интересные задачи», М.1911г.
9. Обреимов В. И. «Математические софизмы», 2-е изд., СПб., 1889г.
литература