Презентация, доклад на тему Шаг за шагом (от базы к профелю)

Задачи на вероятность

Тригонометрические преобразования

Показательные уравнения

Решение:

Случайный эксперимент – бросание жребия.
Элементарное событие – участник, который выиграл жребий.

Число элементарных событий: N=4

Событие А = {жребий выиграл Петя}, N(A)=1

Ответ: 0,25

Алексей
Иван
Татьяна
Ольга

Ответ: 0,5

Решение:

Случайный эксперимент – бросание кубика.
Элементарное событие – число на выпавшей грани.

Ответ:1/3

Всего граней:

1, 2, 3, 4, 5, 6

Элементарные события:

N=6

N(A)=2

Ответ: 0,5

1, 2, 3, 4, 5, 6

Ответ: 0,5

1, 2, 3, 4, 5, 6

Решение:

орел - О

решка - Р

Возможные исходы события:

О

Р

О

О

О

Р

Р

Р

N=4

N(A)=2

Ответ:0,5

4 исхода

Ответ: 0,25

Ответ: 0,25

Решение:

Всего спортсменов: N= 4 + 7 + 9 + 5 = 25

A= {последний из Швеции}

N=25

N(А)=9

Ответ: 0,36

Решение:

Определите N
Определите N(A)

Проверка:

N = 20

N(A)= 20 – 8 – 7 = 5

Ответ: 0,25

A= {первой будет спортсменка из Китая}

Реши самостоятельно!

Ответ: 0,125

Реши самостоятельно!

Ответ: 0,35

Решение:

A={ручка пишет хорошо}

Противоположное событие:

Ответ: 0,9

Решение:

А={вопрос на тему «Вписанная окружность»}
B={вопрос на тему «Параллелограмм»}

События А и В несовместны, т.к. нет вопросов относящихся к двум темам одновременно

С={вопрос по одной из этих тем}

Р(С)=Р(А) + Р(В)

Р(С)=0,2 + 0,15=0,35

Ответ: 0,35

Ответ: 0,52

Решение:

Задача 5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение:

Вероятность попадания = 0,8

Вероятность промаха = 1 - 0,8 = 0,2

А={попал, попал, попал, промахнулся, промахнулся}

По формуле умножения вероятностей

Р(А)= 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2

Р(А)= 0,512 ∙ 0,04 = 0,02048 ≈ 0,02

Ответ: 0,02

Решение:

По формуле умножения вероятностей:

А={хотя бы один автомат исправен}

Ответ: 0,9975

РЕШИТЕ САМОСТОЯТЕЛЬНО

Ответ: - 0,8

Решение: т.к. Sin²α = 1 - cos²α, то
Sin²α = 1 – 0,36 = 0,64
но т.к. π<α<2π, то Sinα < 0
значит Sinα = - √ 0,64 = -0,8

Использована формула: сos 2t = cos2 t – sin2 t

B 11 № 26772. Найдите значение выражения 

Ответ: 12.

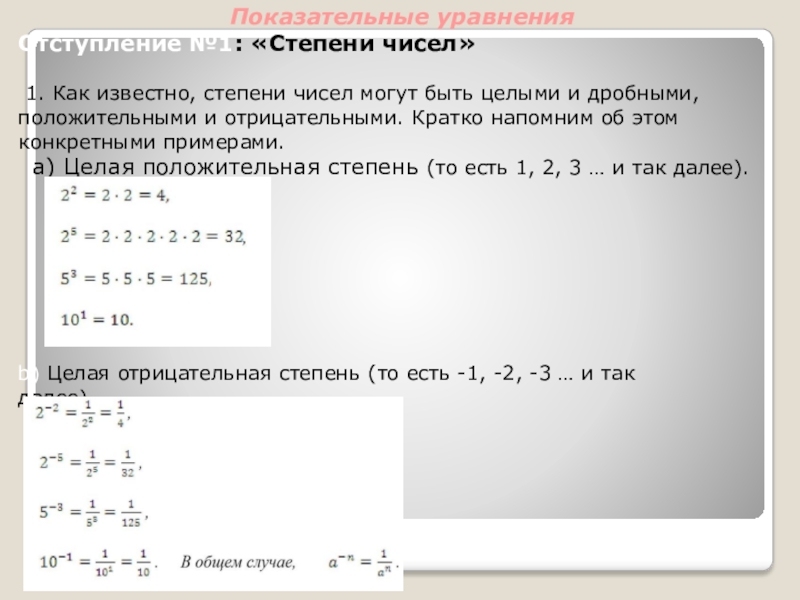
Показательные уравнения

b) Целая отрицательная степень (то есть -1, -2, -3 … и так далее).

c) Дробная положительная степень

и так далее.

Умножать и делить друг на друга можно только числа с одинаковыми основаниями!

Набор формул показывающий, какие действия можно выполнять с двумя и более числами, имеющими степени (то есть любыми числами, указанными в пунктах a) – f)).

уравнение будет выглядеть так:

Подставляем x=14 в исходное уравнение и проверяем, будут ли равны обе части
уравнения:

Действительно, при x=14 , левая часть уравнения равна правой.

Ответ: 14

Тогда будет выглядеть так:

Проверка показала, что корень x=2 найден правильно.


Ответ:2