В группах БУ-21 зд, ЭК-21 зд
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад вводного занятия (дистанционное обучение)
Содержание
- 1. Презентация вводного занятия (дистанционное обучение)
- 2. Пояснительная запискаКурс «Математика» состоит из четырех разделов:1
- 3. Пояснительная запискаКаждый раздел содержит материалы:теоретический и практический
- 4. Прохождение аттестацииЭтапы промежуточной аттестации:– ознакомление с теоретическим
- 5. Порядок выполнения письменных работПисьменную работу выполнить и
- 6. Сроки выполнения письменных работКонтрольную работу и практические
- 7. РАЗДЕЛ 1 ГЛАВА 1. Элементы линейной алгебрыГЛАВА 2. Элементы аналитической геометрии
- 8. Тема 1 Матрицы и определители 1.1 МатрицыМатрица
- 9. Пример: Матрица 2х3 Например, в матрицедве строкии три столбца;
- 10. 1.2 Линейные операции над матрицами
- 11. Пример 1.Пусть даны матрицы
- 12. Пример 2.Пусть даны матрицы
- 13. Умножение матрицы на числоПроизведением матрицы А
- 14. Пусть даны матрицыПроизведением матрицы А на матрицу
- 15. Пусть даны матрицыТребуется найти матрицы АВ и ВА.Пример 1.Решение:Ответ:
- 16. ИмеемВычислить ВАВНИМАНИЕ!Пример 2.Решение:Ответ:
- 17. 2 Определители квадратных матриц Определители второго и
- 18. Пример 1.Решение:Вычислить определитель второго порядкаОтвет: -23
- 19. Определителем третьего порядка называется число, вычисленное по правилу треугольника (Сарруса):Пусть дана матрица третьего порядка
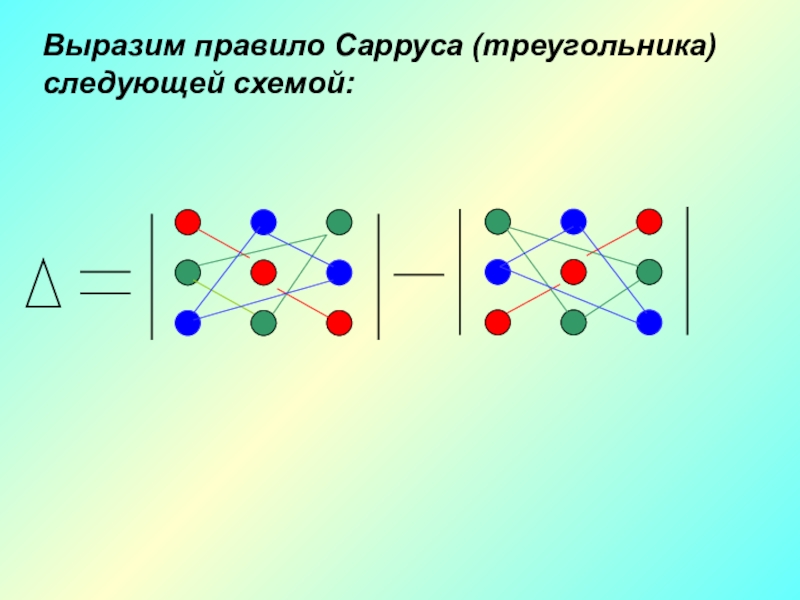
- 20. Выразим правило Сарруса (треугольника) следующей схемой:
- 21. 2. Нахождение определителя классическим способомПусть дана квадратная
- 22. Пусть даны матрицаТребуется найти определитель матрицы А.Пример 1.Решение:Ответ: 45
- 23. Пусть даны матрицаТребуется найти определитель матрицы А разложением по первой строке.Пример 2.Решение:Ответ: 45
- 24. Тема 2 Системы линейных уравненийРассмотрим систему двух линейных уравнений с двумя неизвестными: Положим и если то
- 25. Аналогичногде Габриэл Крамер -швейцарский математик (1704-1752)Определитель Δ
- 26. Решить систему уравнений:Пример.Решение:Ответ: (5; 2)Вычислим определители Δ, Δх, Δу:
- 27. Методы решения систем трёх линейных уравнений с
- 28. РАЗДЕЛ 2 Основы математического анализаГЛАВА 3.
- 29. Глава 3 Введение в анализ. Дифференциальное исчислениеТема
- 30. Тема 3 Теория пределов Предел функции Число
- 31. Пример 1.Вычислить предел Решение:Ответ:при
- 32. Пример 2.Вычислить предел
- 33. Тема 4 Дифференциальное исчисление ПроизводнаяОпределение: Производной функции
- 34. Слайд 34
- 35. .Δх – перемещение телаΔt – промежуток временив течение которого выполнялосьдвижениеМеханический смысл производной.
- 36. Физический смысл: СкоростьускорениеПроизводная от перемещения по времени является мгновенная скорость.Производная от скорости по времени является ускорением.
- 37. Правила дифференцирования 1. Производная суммы равна сумме
- 38. Глава 4 Интегральное исчислениеТема 1: Первообразная и неопределённый интегралТема 2: Определённый интегралТема 3: Дифференциальные уравнения
- 39. Первообразная
- 40. Неопределенный интеграл
- 41. Основные методы интегрированияНепосредственное интегрированиеИнтегрирование заменой переменныхИнтегрирование по частям
- 42. Непосредственное интегрирование (метод разложения)Этот способ интегрирования предполагает
- 43. Слайд 43
- 44. Слайд 44
- 45. Пример 1.Вычислить интеграл Решение:Ответ:
- 46. Метод замены переменнойПусть требуется найти интеграл первообразная
- 47. Пример 1.Вычислить интеграл Решение:Ответ:
- 48. Пример 2.Вычислить интеграл Решение:
- 49. Пример
- 50. Найти Пример 3.
- 51. Интегрирование по частям
- 52. Слайд 52
- 53. Определенный интеграл– формула Ньютона-Лейбница, где xn∈[a; b].Читают:
- 54. Отметим некоторые свойства интеграла (объясните их самостоятельно):Применение
- 55. РАЗДЕЛ 3 Основы теории вероятности и
- 56. Элементы комбинаторики Произведение подряд идущих первых
- 57. Простейшие комбинации
- 58. Пример 1.Решение:Ответ: 56Вычислить
- 59. Пример 2.Решение:Ответ: 1,4Вычислить
- 60. Вероятность случайного событияОпределение. Вероятностью Р(А) события А
- 61. 1. Вероятность случайного события А , есть положительное
- 62. Пример 3.Решение:Ответ: 0,5В урне 10 белых, 5
- 63. Пример 4.Решение:Ответ:Получена партия одежды в количестве 40
- 64. 1. Вероятность суммы двух несовместных событий А и
- 65. 4. Вероятность появления хотя бы одного из
- 66. Формула полной вероятности Формула Байеса Формула Бернулли для повторных независимых испытаний
- 67. Пример 5.Решение:Ответ: 0,1323Вероятность попадания в мишень при
- 68. Литература1 Афанасьева О.Н., Бродский Я.С., Павлов А
Пояснительная запискаКурс «Математика» состоит из четырех разделов:1 Линейная алгебра (с элементами аналитической геометрии)2 Основы математического анализаОсновы теории вероятности и математической статистикиЭлементы линейного программирования
Слайд 1Вводное занятие по дисциплине «Математика»
Новороссийский колледж строительства и экономики
Преподаватель: Татьяна Петровна
Пушкина
Слайд 2Пояснительная записка
Курс «Математика» состоит из четырех разделов:
1 Линейная алгебра (с
элементами аналитической геометрии)
2 Основы математического анализа
Основы теории вероятности и математической статистики
Элементы линейного программирования
2 Основы математического анализа
Основы теории вероятности и математической статистики
Элементы линейного программирования
Слайд 3Пояснительная записка
Каждый раздел содержит материалы:
теоретический и практический (Части I и II)
Часть 1. Основной текст (теория);
Часть 2. Практикум (содержит примеры решения задач и задачи для самостоятельного решения)
Вопросы для самоконтроля
Глоссарий (математический справочник)
Задания и образцы решения помещены в папке «Методические указания»
Слайд 4Прохождение аттестации
Этапы промежуточной аттестации:
– ознакомление с теоретическим материалом;
– просмотр образцов выполнения
самостоятельных работ по предлагаемым темам;
– просмотр Практикумов по данным темам;
– получение необходимой консультации в ЧАТе
– выполнение двух практических работ;
– выполнение одной контрольной работы;
– прохождение контрольного тестирования.
Итоговая аттестация (зачет):
Итоговое тестирование
– просмотр Практикумов по данным темам;
– получение необходимой консультации в ЧАТе
– выполнение двух практических работ;
– выполнение одной контрольной работы;
– прохождение контрольного тестирования.
Итоговая аттестация (зачет):
Итоговое тестирование
Слайд 5Порядок выполнения письменных работ
Письменную работу выполнить и отправить документом Microsoft Word
по электронной почте с обязательным титульным листом и листом «Рецензия преподавателя»
В виду возникающих затруднений с набором математических формул разрешается отправить по электронной почте рукописный вариант письменной работы, выполненный в FineReader (сканированный вариант)
Работу можно выполнить в тетрадном варианте (каждое задание - с новой страницы)
В виду возникающих затруднений с набором математических формул разрешается отправить по электронной почте рукописный вариант письменной работы, выполненный в FineReader (сканированный вариант)
Работу можно выполнить в тетрадном варианте (каждое задание - с новой страницы)
Слайд 6Сроки выполнения письменных работ
Контрольную работу и практические работы необходимо выполнить и
сдать в сроки, обозначенные индивидуальным учебным графиком.
Слайд 8Тема 1 Матрицы и определители
1.1 Матрицы
Матрица - это таблица чисел, состоящая
из m строк и n столбцов:
где i - номер строки, j - номер столбца
Или
,
Слайд 10
1.2 Линейные операции над матрицами
Матрицы одинакового размера можно складывать.
Суммой двух матриц А и В называется такая матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.
Сложение матриц
Слайд 13Умножение матрицы на число
Произведением матрицы А на число
называется матрица, элементы которой равны
произведению числа на соответствующие
элементы матрицы.
Решение:
Ответ:
Пример.
Пусть дана матрица
Вычислить .
Слайд 14Пусть даны матрицы
Произведением матрицы А на матрицу В называется матрица С,
элементы которой составляются следующим образом:
1.3 Умножение матриц
, i = 1, 2, … , m , j = 1, 2, ..., n
Или:
Слайд 172 Определители квадратных матриц
Определители второго и третьего порядка
Определителем второго порядка
называется число,
равное :
равное :
Для квадратных матриц вводится понятие определителя.
Пусть дана матрица
Слайд 19Определителем третьего порядка называется число, вычисленное по правилу треугольника (Сарруса):
Пусть дана
матрица третьего порядка
Слайд 212. Нахождение определителя классическим способом
Пусть дана квадратная матрица третьего порядка, элементы
которой для удобства обозначим через: а1, а2, а3, b1, b2, b3, c1, c2, c3.
Её определитель равен:
Её определитель равен:
Слайд 23
Пусть даны матрица
Требуется найти определитель матрицы А разложением по первой строке.
Пример
2.
Решение:
Ответ: 45
Слайд 24Тема 2 Системы линейных уравнений
Рассмотрим систему двух линейных уравнений
с двумя
неизвестными:
Положим
и если
то
Слайд 25Аналогично
где
Габриэл Крамер -швейцарский математик (1704-1752)
Определитель Δ называется определителем системы двух
линейных уравнений с двумя неизвестными и при этом решение системы находим по формулам Крамера:
Слайд 27Методы решения систем трёх линейных уравнений с тремя неизвестными.
По формулам Крамера
Методом
Гаусса
Методом Жордана-Гаусса
Методом Жордана-Гаусса
Решение системы трех линейных уравнений,
а так же решение матричных уравнений, векторный анализ предлагается рассмотреть самостоятельно, используя теоретический и практический материал, и рекомендуемую литературу
Слайд 28РАЗДЕЛ 2
Основы математического анализа
ГЛАВА 3. Введение в анализ. Дифференциальное исчисление
ГЛАВА
4. Интегральное исчисление функции одной действительной переменной
Слайд 29Глава 3 Введение в анализ. Дифференциальное исчисление
Тема 1: Множества. Действительные числа
Тема
2: Функции действительной переменной
Тема 3: Теория пределов. Непрерывность функции
Тема 4. Дифференциальное исчисление функции одной действительной переменной
Тема 3: Теория пределов. Непрерывность функции
Тема 4. Дифференциальное исчисление функции одной действительной переменной
Слайд 30Тема 3 Теория пределов
Предел функции
Число А называется пределом функции
y =
f(x) в точке (при ), если для любого положительного числа существует число , такое, что для всех допустимых значений аргумента х, удовлетворяющих неравенству
выполняется неравенство
выполняется неравенство
Слайд 33Тема 4 Дифференциальное исчисление
Производная
Определение:
Производной функции в точке х0 называется предел
отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.
Слайд 34
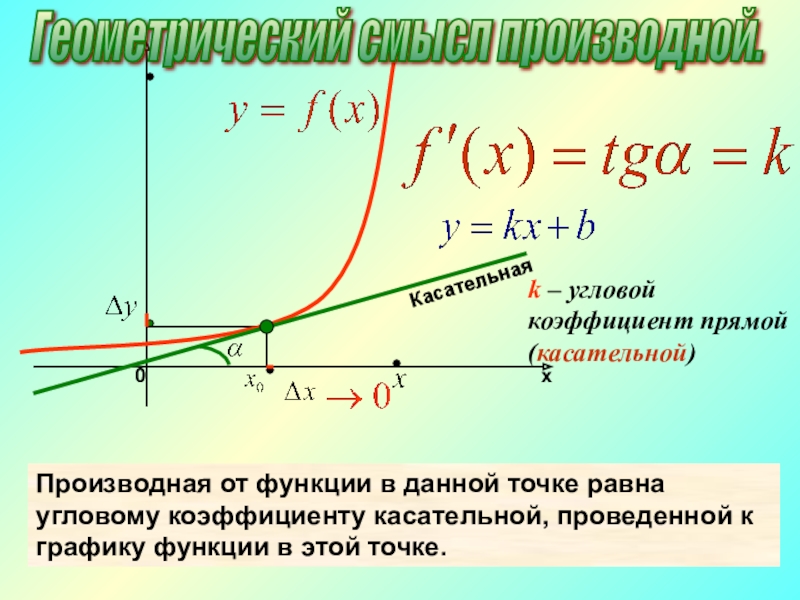
k – угловой
коэффициент прямой(касательной)
Касательная
Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Геометрический смысл производной.
Слайд 35
.
Δх – перемещение тела
Δt – промежуток времени
в течение которого выполнялось
движение
Механический смысл
производной.
Слайд 36 Физический смысл:
Скорость
ускорение
Производная от перемещения по времени является мгновенная скорость.
Производная от скорости
по времени является ускорением.
Слайд 37Правила дифференцирования
1. Производная суммы равна сумме производных,
производная разности равна разности производных:
2.
Постоянный множитель можно вынести за знак
производной:
производной:
3. Производная произведения:
4. Производная частного:
Слайд 38Глава 4 Интегральное исчисление
Тема 1: Первообразная и неопределённый интеграл
Тема 2: Определённый
интеграл
Тема 3: Дифференциальные уравнения
Тема 3: Дифференциальные уравнения
Слайд 41Основные методы интегрирования
Непосредственное интегрирование
Интегрирование заменой переменных
Интегрирование по частям
Слайд 42Непосредственное интегрирование (метод разложения)
Этот способ интегрирования предполагает такое преобразование подынтегральной функции,
которое позволило бы использовать для решения табличные интегралы.
Слайд 46Метод замены переменной
Пусть требуется найти интеграл первообразная которого неизвестна, но известно
что она существует. В этом случае можно попытаться сделать такую замену переменной, чтобы интеграл стал табличным.
где
дифференцируемая функция на множестве Т
Слайд 53Определенный интеграл
– формула
Ньютона-Лейбница
, где xn∈[a; b].
Читают: интеграл от a до
b эф от икс дэ икс.
Для вычисления определённого интеграла применяют:
Число a называют нижним пределом интегрирования, b – верхним пределом интегрирования, f (x) – подынтегральной функцией, x – переменной интегрирования.
Определение:
![Определенный интеграл– формула Ньютона-Лейбница, где xn∈[a; b].Читают: интеграл от a до b эф от икс дэ икс.Для](/img/thumbs/29a744dfce1e723dd03907031499b09b-800x.jpg "Презентация вводного занятия (дистанционное обучение) Определенный интеграл– формула Ньютона-Лейбница, где xn∈[a; b].Читают: интеграл от a до")
Слайд 54Отметим некоторые свойства интеграла (объясните их самостоятельно):
Применение этих свойств часто упрощает
вычисление интегралов.
, где c∈
Пример 1
Пример 2
Слайд 55РАЗДЕЛ 3
Основы теории вероятности и математической статистики
ГЛАВА 5. Элементы теории
вероятностей
ГЛАВА 6. Элементы математической статистики
ГЛАВА 6. Элементы математической статистики
Слайд 56Элементы комбинаторики
Произведение подряд идущих первых n натуральных чисел обозначают
n! и называют «эн факториал»:
n! = 1 × 2 × 3 × 4 ×...×(n - 2)×(n – 1)×n.
«factor» - «множитель»
«эн факториал» - «состоящий из n множителей».
Например, 7! = 1 × 2 × 3 × 4 ×5 × 6 × 7 = 840
n! = 1 × 2 × 3 × 4 ×...×(n - 2)×(n – 1)×n.
«factor» - «множитель»
«эн факториал» - «состоящий из n множителей».
Например, 7! = 1 × 2 × 3 × 4 ×5 × 6 × 7 = 840
Определение.
Слайд 60Вероятность случайного события
Определение. Вероятностью Р(А) события А называется отношение числа благоприятствующих
исходов т к общему числу n равновозможных несовместных исходов n:
Слайд 611. Вероятность случайного события А , есть положительное число, заключённое между 0
и 1.
0 ≤ Р(А) ≤ 1.
2. Вероятность достоверного события равна единице.
3. Вероятность невозможного события равна нулю.
0 ≤ Р(А) ≤ 1.
2. Вероятность достоверного события равна единице.
3. Вероятность невозможного события равна нулю.
Свойства вероятности:
Слайд 62Пример 3.
Решение:
Ответ: 0,5
В урне 10 белых, 5 красных и 5 зеленых
шаров. Найти вероятность того, что вынутый наугад шар будет цветным (не белым).
Число исходов, благоприятствующих событию А, равно сумме красных и зеленых шаров: т = 10. Общее число равновозможных несовместных исходов равно общему числу шаров в урне: n = 20. Тогда:
Слайд 63Пример 4.
Решение:
Ответ:
Получена партия одежды в количестве 40 штук. Из них 20
комплектов мужской одежды, 6 - женской и 14 -детской. Найти вероятность того, что взятая наугад одежда окажется не женской.
Событие А - одежда мужская, вероятность
Событие В - одежда женская,
Событие С- одежда детская,
Тогда
Слайд 641. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей
этих событий:
Р(А +В) = Р(А) + Р(В).
2. Если события А1, А2,..., Аn . образуют полную группу, то сумма их вероятностей равна единице, т е.
3. Сумма вероятностей противоположных событий равна единице, т.е.
Р(А +В) = Р(А) + Р(В).
2. Если события А1, А2,..., Аn . образуют полную группу, то сумма их вероятностей равна единице, т е.
3. Сумма вероятностей противоположных событий равна единице, т.е.
Теоремы вероятностей
Слайд 654. Вероятность появления хотя бы одного из двух совместных
событий равна сумме
вероятностей этих событий без
вероятности их совместного наступления, т.е.
Р(А +В) = Р(А) + Р(В) – P(A × B).
5. Вероятность произведения двух независимых событий А и
В равна произведению вероятностей этих событий
Р(А и В) = Р(А×В) = Р(А) ∙Р(В).
6. Вероятность произведения двух зависимых событий равна
произведению вероятность одного из них на условную
вероятность другого, вычисленную при условии, что первое
событие осуществилось:
вероятности их совместного наступления, т.е.
Р(А +В) = Р(А) + Р(В) – P(A × B).
5. Вероятность произведения двух независимых событий А и
В равна произведению вероятностей этих событий
Р(А и В) = Р(А×В) = Р(А) ∙Р(В).
6. Вероятность произведения двух зависимых событий равна
произведению вероятность одного из них на условную
вероятность другого, вычисленную при условии, что первое
событие осуществилось:
Теоремы вероятностей
Слайд 66Формула полной вероятности
Формула Байеса
Формула Бернулли для повторных независимых испытаний
Слайд 67Пример 5.
Решение:
Ответ: 0,1323
Вероятность попадания в мишень при одном выстреле для данного
стрелка равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.
Поскольку , то . По условию ,
.
По формуле Бернулли :
Слайд 68Литература
1 Афанасьева О.Н., Бродский Я.С., Павлов А Математика для техникумов -
М., Наука, 1991
2 Валуцэ И.И. Математика для техникумов : учебное пособие М.: Наука, 1990.
3 Гмурман В. Е. Теория вероятностей и математическая статистика. – М.: Издательство МГУ, 2001.
4 Дадаян А. А. Математика: учебник -М.: Форум: ИНФРА-М, 2005.
5 Ильин В. А. Основы математического анализа: в 2 т. - М.: Наука:
Физматлит, 2001.
6 Солодовников А. С., Торопов Г. А. Линейная алгебра с элементами аналитической геометрии. - М.: Высшая школа, 1987.
7 Шипачев В. С. Высшая математика: учебник-М.: Высшая школа, 2000.
8 Электронный носитель. Учебник для ДО. - 2006.
2 Валуцэ И.И. Математика для техникумов : учебное пособие М.: Наука, 1990.
3 Гмурман В. Е. Теория вероятностей и математическая статистика. – М.: Издательство МГУ, 2001.
4 Дадаян А. А. Математика: учебник -М.: Форум: ИНФРА-М, 2005.
5 Ильин В. А. Основы математического анализа: в 2 т. - М.: Наука:
Физматлит, 2001.
6 Солодовников А. С., Торопов Г. А. Линейная алгебра с элементами аналитической геометрии. - М.: Высшая школа, 1987.
7 Шипачев В. С. Высшая математика: учебник-М.: Высшая школа, 2000.
8 Электронный носитель. Учебник для ДО. - 2006.
