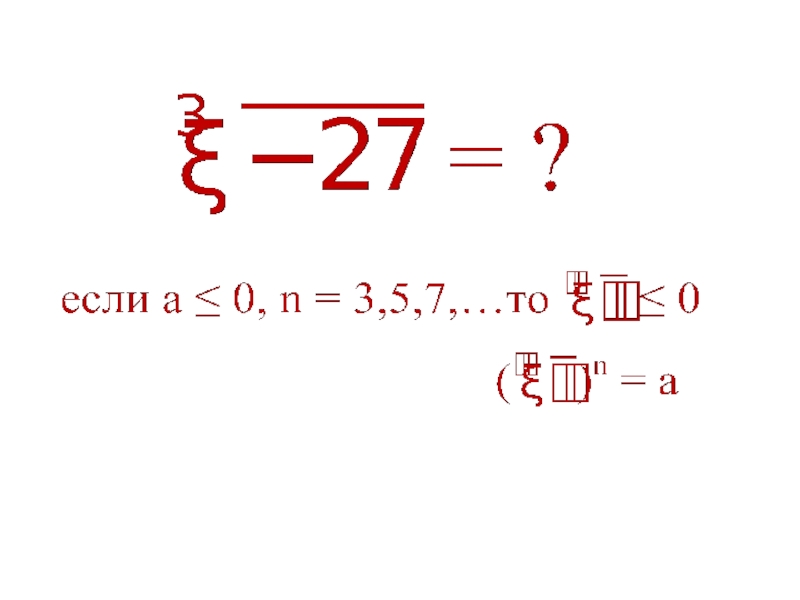- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока Корень п-й степени из действительного числа
Содержание
- 1. Презентация урока Корень п-й степени из действительного числа
- 2. «Тяжело на уроке, легко на экзамене…»
- 3. Слайд 3
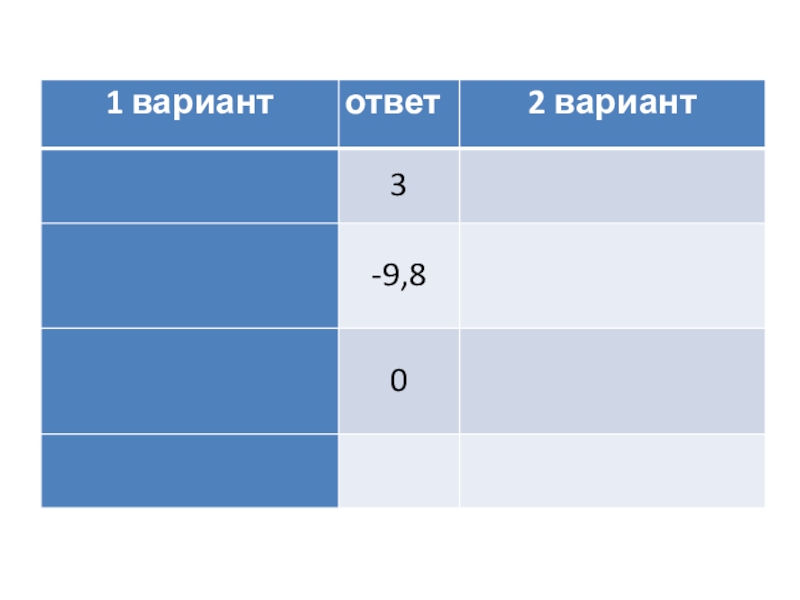
- 4. 2. a2= 64; a2=0,04; a2=0,1; a2=-25
- 5. Слайд 5
- 6. Слайд 6
- 7. Понятие корня п-ой степени из действительного числа
- 8. Выражение:Знак корня (знак радикала) в математике — условное обозначение для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак используется для кубических корней, — для корней4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение .ИсторияЗнак корня происходит из строчной латинской буквы r (начальной в лат. radix — корень), сросшейся с надстрочной чертой: в старину надчёркивание выражения использовались вместо нынешнего заключения его в скобки, так что есть всего лишь видоизменённый древний способ записи чего-то вроде .Впервые такое обозначение использовал немецкий математик Томас Рудольф в 1525 году.называют радикалом (от латинского слова радикс, что означает «корень»).
- 9. Слайд 9
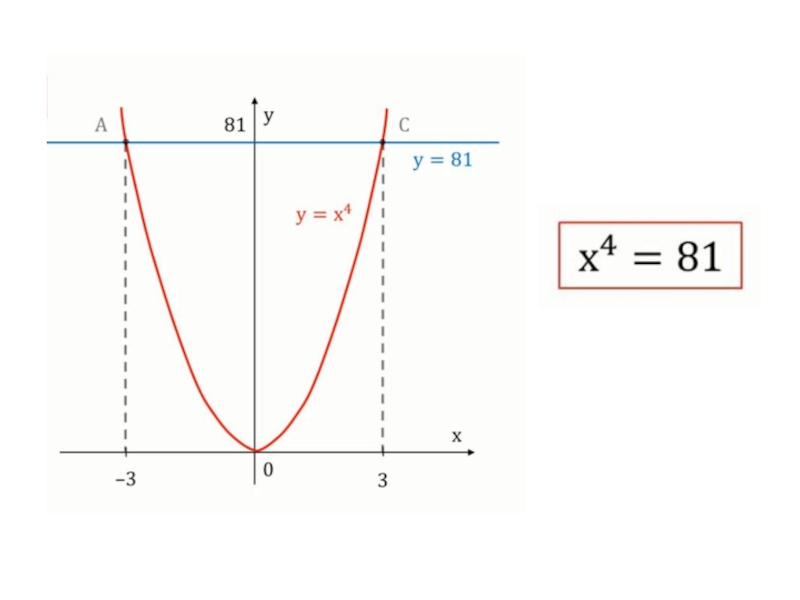
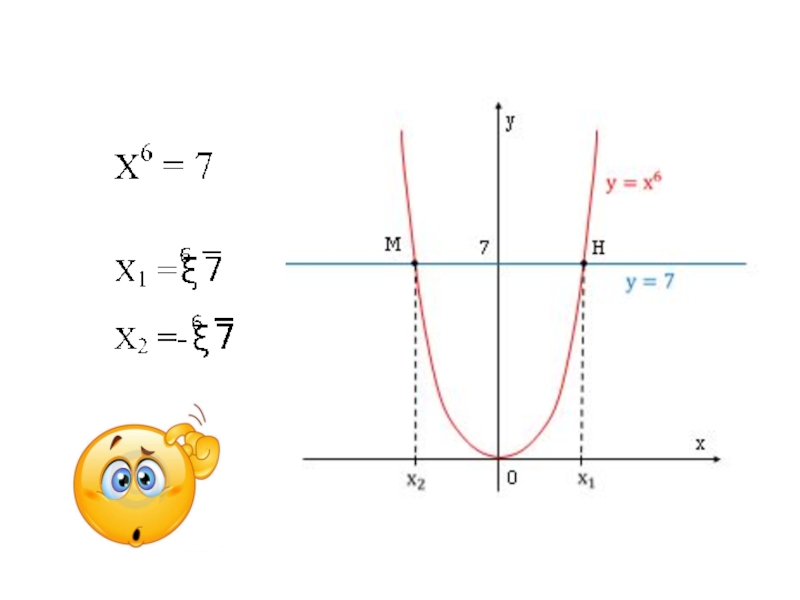
- 10. Корень n-ой степени из числаa ≥ 0, n ≥ 2если:
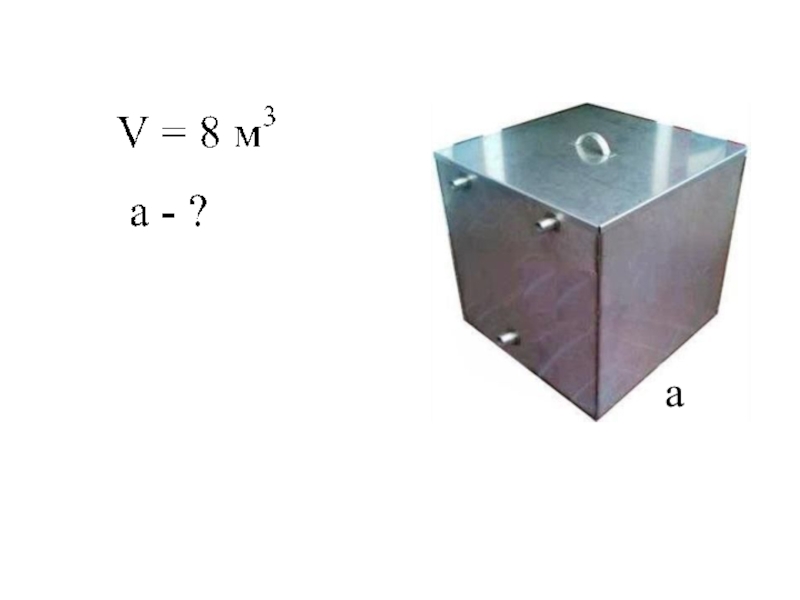
- 11. № 3341.2.
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. a
- 18. 1. С каким математическим понятием мы работали
- 19. Слайд 19
- 20. Слайд 20
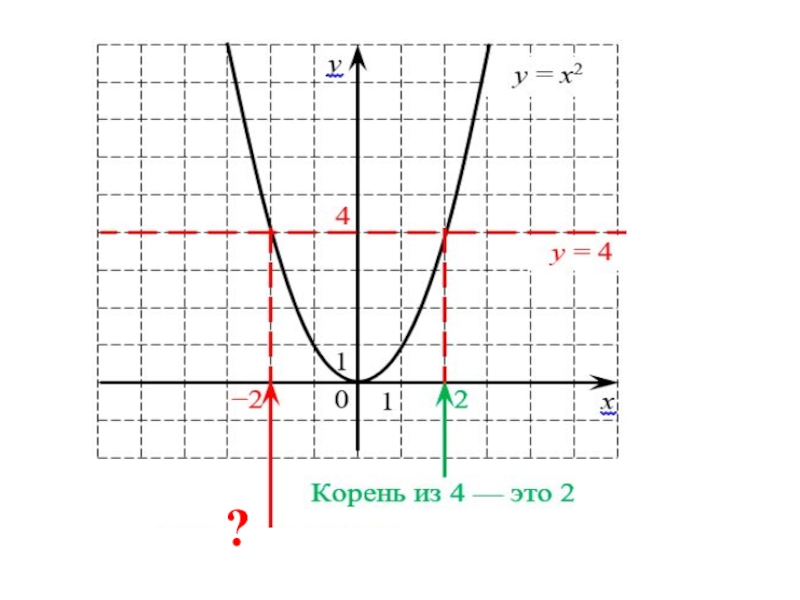
- 21. ?
- 22. Слайд 22
«Тяжело на уроке, легко на экзамене…»
Слайд 8Выражение:
Знак корня (знак радикала) в математике — условное обозначение для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак используется для кубических корней, — для корней4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение .
История
Знак корня происходит из строчной латинской буквы r (начальной в лат. radix — корень), сросшейся с надстрочной чертой: в старину надчёркивание выражения использовались вместо нынешнего заключения его в скобки, так что есть всего лишь видоизменённый древний способ записи чего-то вроде .
Впервые такое обозначение использовал немецкий математик Томас Рудольф в 1525 году.
называют радикалом (от латинского слова радикс, что
означает «корень»).
Слайд 181. С каким математическим понятием мы работали сегодня
корень n–ой степени
2. Что мы применяли для вычислений корня n–ой степени
оределение корня n–ой степени
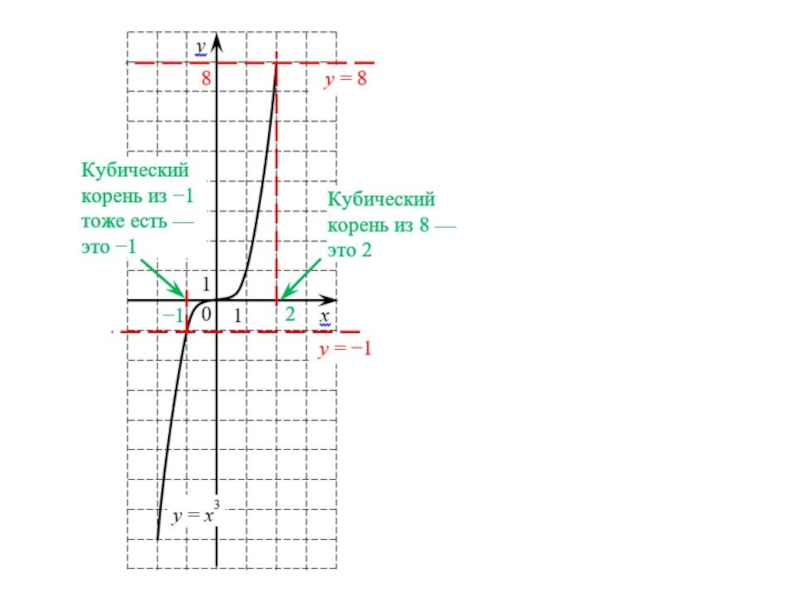
3. Сколько корней имеет уравнение хn = а, если n – нечетное число (например: х7 = 5)
один корень
4. Сколько корней имеет уравнение хn= а, если n –четное число (например: х12=а)
зависит от а:
если а – отрицательное, то нет корней;
если а = 0, то один корень;
если а – положительное, то два корня.
2. Что мы применяли для вычислений корня n–ой степени
оределение корня n–ой степени
3. Сколько корней имеет уравнение хn = а, если n – нечетное число (например: х7 = 5)
один корень
4. Сколько корней имеет уравнение хn= а, если n –четное число (например: х12=а)
зависит от а:
если а – отрицательное, то нет корней;
если а = 0, то один корень;
если а – положительное, то два корня.