- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по ТОНКМ с методикой обучения на тему Математические понятия
Содержание
- 1. Презентация по ТОНКМ с методикой обучения на тему Математические понятия
- 2. В начальном курсе математики
- 3. Понятие – это форма
- 4. Существенные и несущественные свойства
- 5. 1. Противоположенные стороны 2.
- 6. Существенные свойства – это
- 7. Слайд 7
- 8. Объем понятия – множество
- 9. Рассмотрим понятие «треугольник» и «прямоугольный треугольник»
- 10. Объем понятия «треугольник» больше
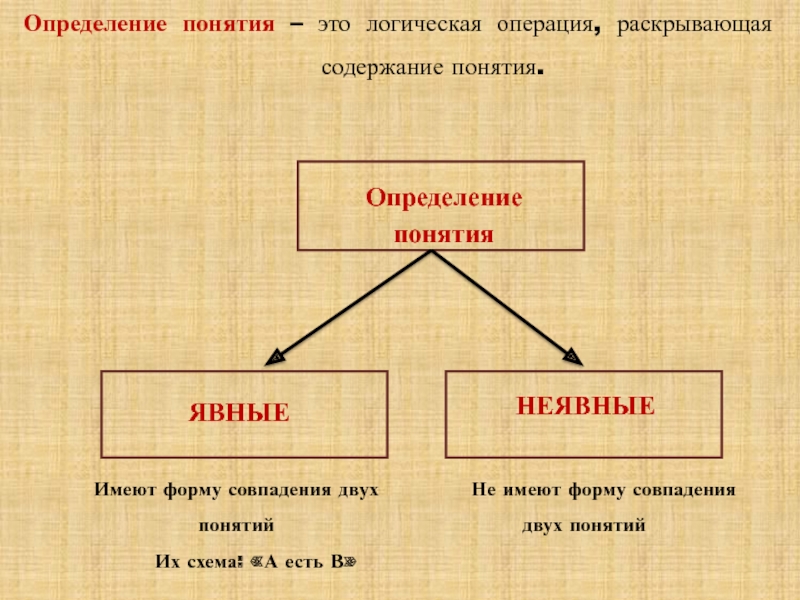
- 11. Определение понятия – это логическая операция, раскрывающая содержание понятия.
- 12. Пример: Квадрат – это
- 13. Пример: Определение. Дробь, у
- 14. Генетическое определение – указан
- 15. 3. Отрицательные определения -
- 16. Слайд 16
- 17. Слайд 17
- 18. В начальной школе в
- 19. Пример: Квадрат – это четырехугольник, у которого
- 20. Запрещается порочный круг, то есть
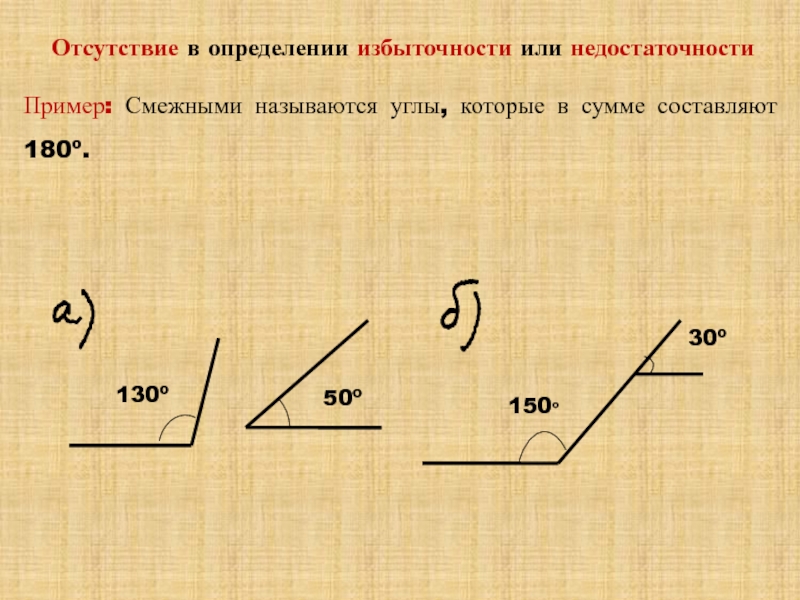
- 21. Отсутствие в определении избыточности или недостаточностиПример: Смежными называются углы, которые в сумме составляют 180º.
- 22. Сумма данных углов составляет
- 23. Пример. Квадратом называется прямоугольник, у которого все
Слайд 1
Математические понятия
План
Профессиональный аспект темы
Математическое понятие:
Существенные и несущественные
Объем понятия.
Содержание понятия.
Связь между объемом и содержанием.
Определение понятий:
Виды определений.
Требования к определению понятий.
Алгоритм построения определения понятия.
Основные выводы
Слайд 2
В начальном курсе математики изучаются различные понятия, которые
числа и операции над ними;
алгебраические понятия;
геометрические понятия;
величины и их измерение.
Учителю необходимы теоретические знания о видах и структуре определений математических понятий и объектов для того, чтобы осуществлять процесс формирования понятий у учащихся.
Слайд 3
Понятие – это форма мышления о целостной совокупности
Математические понятия имеют особенности: математические объекты, о которых составляют понятие, в реальности не существуют.
Пример: В геометрии изучается форма и размер предметов, но не изучается их масса, цвет и т.д., поэтому вместо «предмет» говорят «геометрическая фигура».
Слайд 5
1. Противоположенные стороны
2. Углы прямые
3. Противоположенные стороны
4. Диагонали равны
5. Диагонали точкой пересечения делятся пополам
6. Диагональ делит на два равных треугольника
2. MNKL – прямоугольник
АВСД – прямоугольник
4. MNKL – красный
3. АВСД – синий
5. АВ, СД – большая сторона
7. АД – меньшая сторона
6. MK, NL – большая сторона
8. KL – меньшая сторона
Слайд 6
Существенные свойства – это свойства, присущие данному объекту,
Несущественные свойства – это свойства, отсутствие которых не влияет на существование объекта.
Математическое понятие – это совокупность всех существенных свойств объекта.
Слайд 8
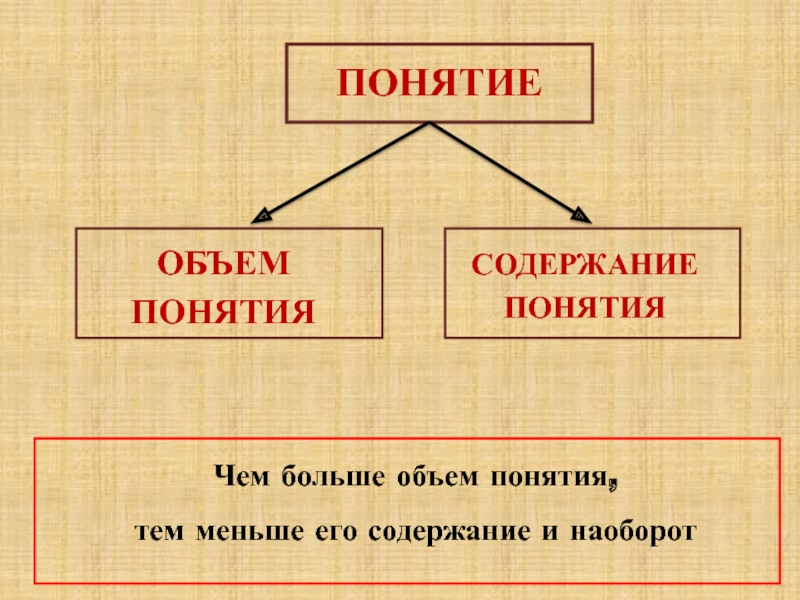
Объем понятия – множество всех объектов, обозначаемых одним
Содержание понятия – множество всех существенных свойств объекта.
Характеристика понятия –
термин,
объем,
содержание.
Пример. Дать характеристику понятию «квадрат».
Термин – квадрат
Объем понятия – множество различных квадратов
Содержание – четыре прямых угла, равные стороны, равные диагонали…
Слайд 10
Объем понятия «треугольник» больше объема понятия «прямоугольный треугольник»,
Слайд 12
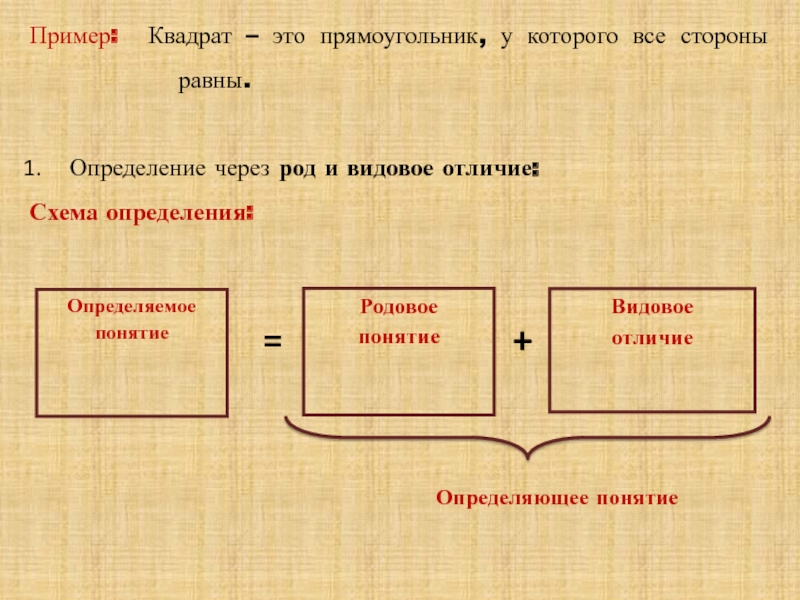
Пример: Квадрат – это прямоугольник, у которого все
Определение через род и видовое отличие:
Схема определения:
Слайд 13
Пример:
Определение. Дробь, у которой числитель меньше знаменателя,
Определяемое понятие – правильная дробь (термин)
Родовое понятие – дробь
Видовое отличие – числитель меньше знаменателя.
Слайд 14
Генетическое определение – указан способ происхождения данного понятия.
Пример:
Термин – треугольник
Род – фигура
Способ построения – взять три точки, не лежащие на одной прямой и соединить каждую пару отрезками.
Слайд 15
3. Отрицательные определения - не задают свойства объекта,
Пример: Скрещивающиеся прямые - это прямые которые не лежат в одной плоскости.
Определяемое понятие – скрещивающиеся прямые
Родовое понятие – прямые
Видовое отличие – не лежат в одной плоскости.
Слайд 18
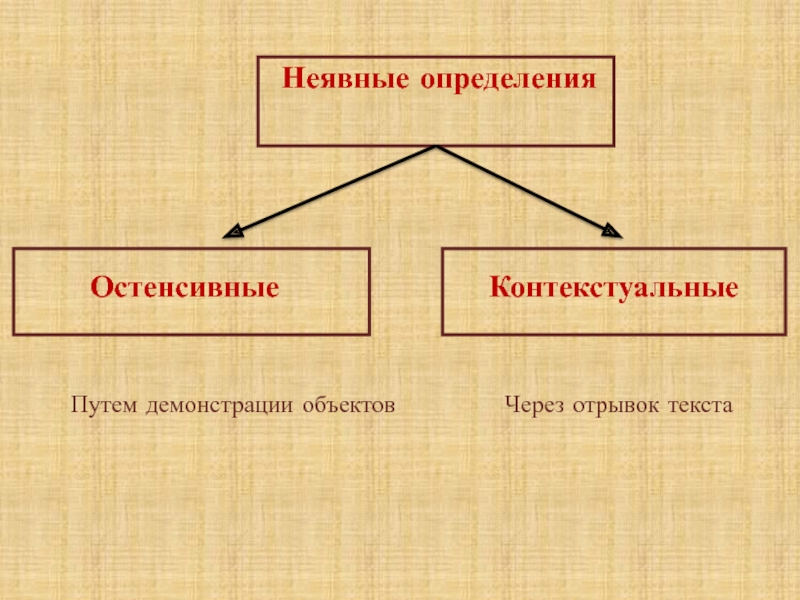
В начальной школе в основном используются неявные определения.
Требования к определению понятия:
1. Определение должно быть соразмерным, то есть объемы определяемого и определяющего понятия должны совпадать.
Слайд 19Пример: Квадрат – это четырехугольник, у которого все стороны равны.
Определяемое
Объем – множество квадратов
Определяющее понятие – четырехугольник – множество четырехугольников, у которых все стороны равны, а это множество ромбов.
Но не всякий ромб есть квадрат, то есть объемы понятий не совпадают определение несоразмерно.
Слайд 20 Запрещается порочный круг, то есть нельзя определять через само
Пример: Равные треугольники – это треугольники которые равны.
Умножение чисел – это действие при помощи которого находят произведение чисел.
Слайд 21Отсутствие в определении избыточности или недостаточности
Пример: Смежными называются углы, которые в
Слайд 22
Сумма данных углов составляет 180º, но они не
одна сторона общая
две другие являются продолжением одна другой
Слайд 23Пример. Квадратом называется прямоугольник, у которого все стороны равны и углы
Избыточное свойство – «иметь прямые углы».
Задание:
Назвать определяемое понятие (термин)
Указать ближайшее родовое понятие
Сформулировать видовое отличие
Проверить выполнены ли требования к определению понятия.