оси вращения»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по ПМ 01. МДК 01.04 Раздел 4.1 Электрический привод для специальности 13.02.11 на тему Приведение движения электропривода к одной оси вращения
Содержание
- 1. Презентация по ПМ 01. МДК 01.04 Раздел 4.1 Электрический привод для специальности 13.02.11 на тему Приведение движения электропривода к одной оси вращения
- 2. Расчетные схемы механической части электропривода:Механическая часть электропривода
- 3. Расчетные схемы механической части электропривода:Обычно в качестве
- 4. Приведение моментов сопротивления и сил к валу
- 5. Приведение моментов сопротивления и сил к валу
- 6. Приведение моментов инерции к валу электродвигателя:
- 7. Учет потерь в передачах:Потери энергии (мощности) в
- 8. Учет потерь в передачах:СледовательноМс↑ = (Мм ωм)
- 9. Задача на приведение момента инерции к валу
- 10. Задача на приведение момента инерции к валу
- 11. Решение:1. Определим скорость подъема груза Vм: Vм =
- 12. Контрольные вопросы:С какой целью осуществляется приведение моментов
Расчетные схемы механической части электропривода:Механическая часть электропривода (ЭП) может представлять сложную кинематическую схему с большим числом движущихся элементов, при этом одни элементы совершают вращательное движение, другие – поступательное (например, в подъемниках, кранах, строгальных станках и др.).
Слайд 1Лекция №3 по дисциплине «Теория электропривода»
Тема: «Приведение движения электропривода к одной
Слайд 2Расчетные схемы механической части электропривода:
Механическая часть электропривода (ЭП) может представлять сложную
кинематическую схему с большим числом движущихся элементов, при этом одни элементы совершают вращательное движение, другие – поступательное (например, в подъемниках, кранах, строгальных станках и др.). Каждый элемент обладает определенной упругостью (т.е. под нагрузкой может деформироваться), а в соединительных элементах могут быть воздушные зазоры. Значит, механическая схема ЭП является многомассовой, с упругими связями и зазорами, расчет динамики которой составляет определенные трудности (нужно использовать программы расчетов на ЭВМ).
В инженерных расчетах, не требующих большой точности, в системах с незначительными упругостями элементов и небольшими зазорами (т.е. с большой жесткостью) принимают допущение, что механические связи элементов являются абсолютно жесткими. При таком допущении движение одного элемента дает полную информацию о движении и других элементов.
В инженерных расчетах, не требующих большой точности, в системах с незначительными упругостями элементов и небольшими зазорами (т.е. с большой жесткостью) принимают допущение, что механические связи элементов являются абсолютно жесткими. При таком допущении движение одного элемента дает полную информацию о движении и других элементов.
Слайд 3Расчетные схемы механической части электропривода:
Обычно в качестве такого первоначального элемента принимают
вал двигателя. Тогда расчетная схема механизма многомассовой механической части ЭП (рис. 1, а, 2, а) сводится к одному обобщенному жесткому механическому звену (рис. 1, б, 2, б), имеющему эквивалентную массу с моментом инерции J, угловую скорость вращения ω, угол поворота φ, и на которое звено действуют электромагнитный момент двигателя М и суммарный приведенный к валу двигателя статический момент сопротивления Мс (включающий все механические потери в системе, в том числе и в двигателе).
Рис.1
Рис.2
Слайд 4Приведение моментов сопротивления и сил к валу электродвигателя:
Сначала примем допущение, что
передаточный механизм ПМ (рис. 1, а) идеальный, т.е. не имеет потерь энергии, не обладает массой и осуществляет только количественное преобразование механической энергии от двигателя к производственному механизму. Учет потерь в ПМ рассмотрим несколько позже.
Приведение статических моментов сопротивления к валу осуществляется из условия равенства передаваемой мощности на любом валу (см. рис. 1, а):
Мс ω = Мм ωм.
Из этого равенства находим выражение для определения приведенного статического момента Мс:
Мс = Мм(ωм / ω ) = Мм /(ω / ωм) = Мм / i,
где i = ω / ωм – передаточное число ПМ.
Следовательно, статический момент на валу электродвигателя при отсутствии потерь в ПМ равен моменту сопротивления Мм на валу исполнительного механизма (ИМ), деленному на передаточное число i ПМ. В этом и заключается приведение момента сопротивления ИМ к валу электродвигателя.
Приведение статических моментов сопротивления к валу осуществляется из условия равенства передаваемой мощности на любом валу (см. рис. 1, а):
Мс ω = Мм ωм.
Из этого равенства находим выражение для определения приведенного статического момента Мс:
Мс = Мм(ωм / ω ) = Мм /(ω / ωм) = Мм / i,
где i = ω / ωм – передаточное число ПМ.
Следовательно, статический момент на валу электродвигателя при отсутствии потерь в ПМ равен моменту сопротивления Мм на валу исполнительного механизма (ИМ), деленному на передаточное число i ПМ. В этом и заключается приведение момента сопротивления ИМ к валу электродвигателя.
Слайд 5Приведение моментов сопротивления и сил к валу электродвигателя:
При поступательном движении ИМ
(см. рис. 2, а) и допущении об идеальности передачи из условия равенства передаваемой мощности от электродвигателя ЭД к поднимаемому грузу имеем равенство
Мс ω = Fc V,
где Мс – эквивалентный статический момент на валу ЭД одномассовой системы (см. рис. 2, б);
Fc – сила сопротивления в установившемся режиме;
V – линейная скорость подъема груза.
Тогда из этого равенства получаем
Мс = Fc V / ω = Fc ρ,
где ρ – радиус приведения поступательного движения к вращательному.
Мс ω = Fc V,
где Мс – эквивалентный статический момент на валу ЭД одномассовой системы (см. рис. 2, б);
Fc – сила сопротивления в установившемся режиме;
V – линейная скорость подъема груза.
Тогда из этого равенства получаем
Мс = Fc V / ω = Fc ρ,
где ρ – радиус приведения поступательного движения к вращательному.
Слайд 7Учет потерь в передачах:
Потери энергии (мощности) в ПМ учитывают двумя способами:
приближенным (с помощью КПД)
уточненным (путем вычисления всех составляющих потерь).
Рассмотрим первый способ.
Механическая часть ЭП включает ротор ЭД, вращающийся с угловой скоростью ω и приложенным моментом М, передаточный механизм ПМ с КПД ηп и передаточным числом i и исполнительный механизм ИМ, вращающийся со скоростью ωм и приложенным моментом сопротивления Мм. При направлении энергии от ЭД к ИМ имеем двигательный режим работы ЭП, а при обратном потоке энергии – тормозной. В установившемся режиме работы ЭП, который мы и будем рассматривать для учета потерь в ПМ, движущий момент М на валу ЭД равен приведенному к валу статическому моменту Мс, который учитывает момент сопротивления Мм ИМ и момент потерь в ПМ, т.е. М = Мс. Для наглядности обозначим Мс в двигательном режиме ЭП через Мс↑, а в тормозном – через Мс↓. Тогда, исходя из закона сохранения энергии, можно записать равенства:
ω Мс↑ ηп = Мм ωм для двигательного режима,
Мм ωм ηп = Мс↓ ω для тормозного режима,
Слайд 8Учет потерь в передачах:
Следовательно
Мс↑ = (Мм ωм) / (ω ηп) =
Мм / (i ηп) = Мм' / ηп,
Мс↓ = Мм ωм ηп / ω = Мм ηп / i = Мм' ηп,
где Мм' – момент ИМ, приведенный к валу ЭД без учета потерь в ПМ.
Мс↓ = Мм ωм ηп / ω = Мм ηп / i = Мм' ηп,
где Мм' – момент ИМ, приведенный к валу ЭД без учета потерь в ПМ.
Слайд 9Задача на приведение момента инерции к валу двигателя:
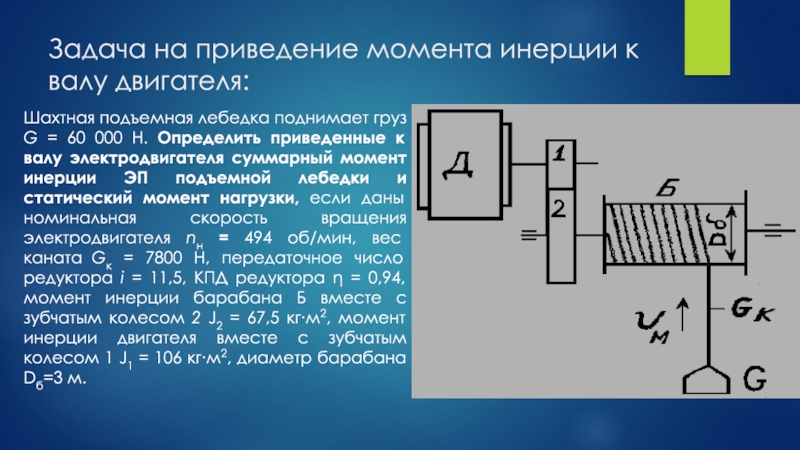
Шахтная подъемная лебедка поднимает
груз G = 60 000 H. Определить приведенные к валу электродвигателя суммарный момент инерции ЭП подъемной лебедки и статический момент нагрузки, если даны номинальная скорость вращения электродвигателя nн = 494 об/мин, вес каната Gк = 7800 Н, передаточное число редуктора i = 11,5, КПД редуктора η = 0,94, момент инерции барабана Б вместе с зубчатым колесом 2 J2 = 67,5 кг∙м2, момент инерции двигателя вместе с зубчатым колесом 1 J1 = 106 кг∙м2, диаметр барабана Dб=3 м.
Слайд 10Задача на приведение момента инерции к валу двигателя:
1. Определим скорость подъема
груза Vм:
Vм = π Dб nн / (i 60)
2. Определим суммарный приведенный к валу электродвигателя момент инерции подъемной лебедки:
J = J1 + J2 / i2 + ((G + Gк) / g2)(Vм / ωн)2
где ωн = 2π nн / 60
3. Приведенный к валу электродвигателя момент сопротивления нагрузки:
Мс↑ = (G + Gк) Rб / (i η)
или
Мс↑ = ((G + Gк) / 10) ρ / η
Vм = π Dб nн / (i 60)
2. Определим суммарный приведенный к валу электродвигателя момент инерции подъемной лебедки:
J = J1 + J2 / i2 + ((G + Gк) / g2)(Vм / ωн)2
где ωн = 2π nн / 60
3. Приведенный к валу электродвигателя момент сопротивления нагрузки:
Мс↑ = (G + Gк) Rб / (i η)
или
Мс↑ = ((G + Gк) / 10) ρ / η
Слайд 11Решение:
1. Определим скорость подъема груза Vм:
Vм = 3,14 ∙ 3 ∙
494 / (11,1 ∙ 60) = 6,75 м/с.
2. Определим суммарный приведенный к валу электродвигателя момент инерции подъемной лебедки:
J = 106 + 67,5/(11,5)2 + ((60 000 + 7 800) / (9,81)2 ∙(6,75 / 51,7)2) = 118,4 кг∙м2,
где ωн = 3,14 ∙ 494 / 30 = 51,7 рад/с.
3. Приведенный к валу электродвигателя момент сопротивления нагрузки:
Мс↑ = (60 000 + 7 800)∙1,5 / (11,5∙0,94) = 9 400 Н∙м
или
Мс↑ = (60 000 + 7 800) / 10 ∙ 6,75 / 51,7 / 0,94 = 9 400 Нм.
2. Определим суммарный приведенный к валу электродвигателя момент инерции подъемной лебедки:
J = 106 + 67,5/(11,5)2 + ((60 000 + 7 800) / (9,81)2 ∙(6,75 / 51,7)2) = 118,4 кг∙м2,
где ωн = 3,14 ∙ 494 / 30 = 51,7 рад/с.
3. Приведенный к валу электродвигателя момент сопротивления нагрузки:
Мс↑ = (60 000 + 7 800)∙1,5 / (11,5∙0,94) = 9 400 Н∙м
или
Мс↑ = (60 000 + 7 800) / 10 ∙ 6,75 / 51,7 / 0,94 = 9 400 Нм.
Слайд 12Контрольные вопросы:
С какой целью осуществляется приведение моментов электропривода к одной оси
вращения?
С какой целью и как осуществляется приведение моментов инерции электропривода к одной оси вращения?
Что такое радиус приведения? В каком случае он используется при приведении момента инерции?
Как учитывается КПД исполнительного механизма при работе привода в двигательном режиме? В тормозном (генераторном) режиме?
С какой целью и как осуществляется приведение моментов инерции электропривода к одной оси вращения?
Что такое радиус приведения? В каком случае он используется при приведении момента инерции?
Как учитывается КПД исполнительного механизма при работе привода в двигательном режиме? В тормозном (генераторном) режиме?