- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Числа Фибоначчи
Содержание
- 1. Презентация по математике Числа Фибоначчи
- 2. Актуальность темы. В мире есть закономерности, которые
- 3. Последовательность Фибоначчи проиллюстрирована самой природой. Эта
- 4. После Фибоначчи осталось большое число задач.
- 5. Числа Фибоначчи 1, 1, 2, 3,
- 6. 1, 1, 2, 3, 5, 8, 13,
- 7. Если принять центром человеческого тела точку пупа,
- 8. Пропорция φ обычно отмечается в тех местах,
- 9. Слайд 9
- 10. Слайд 10
- 11. Числа Фибоначчи в живой природе. Чёткая,
- 12. Цикорий-21 леп.
- 13. Гипотеза.Необычное явление, как числа Фибоначчи, не
- 14. Цели :Изучить числовую последовательность Фибоначчи ;Найти примеры использования чисел Фибоначчи в окружающем нас мире.
- 15. Задачи:Изучить литературу по данной теме. Описать числовой
- 16. Астеническое телосложение Астеническое телосложение подразумевает природную худобу
- 17. Слайд 17
- 18. Нормостеническое телосложение Нормостеник обладает пропорциональной мышечной
- 19. Слайд 19
- 20. Гиперстеническое телосложение Гиперстеники обладают округлыми формами, у
- 21. Слайд 21
- 22. ВыводыПроанализировав результаты, представленные в таблицах, можно с
- 23. ЗаключениеМы убедились, что у Природы есть свои
- 24. Список литературы и сайтов.1. Воробьев Н. Н.
- 25. Спасибо за внимание.
Слайд 1
Загадка чисел
Фибоначчи
автор: Верёменко Валерия, учащаяся 7 «Б
МОБУ СОШ
Слайд 2Актуальность темы.
В мире есть закономерности, которые могут быть описаны с
Попытаемся проникнуть за завесу тайны создания нашей Вселенной.
Слайд 3 Последовательность Фибоначчи проиллюстрирована самой природой. Эта последовательность, известная всем по фильму «Код
Извечное стремление человека познать себя и окружающий мир двигало науку вперёд.
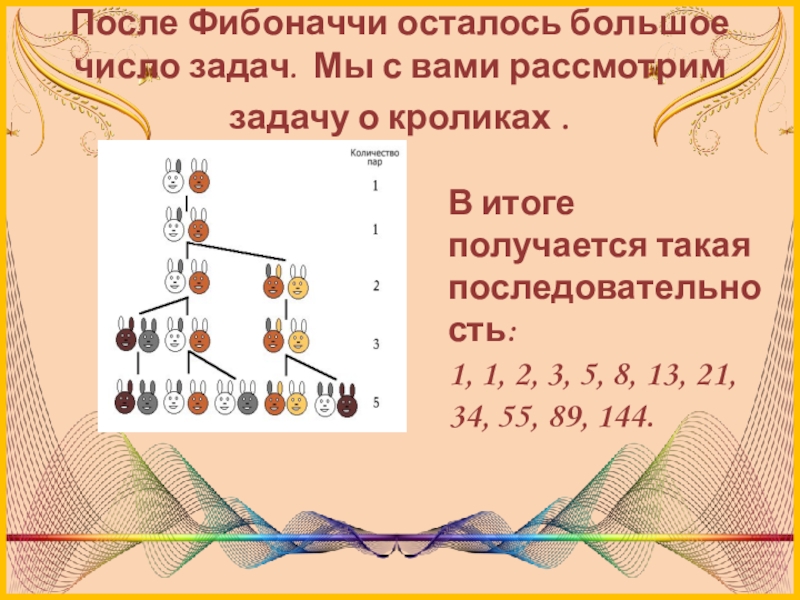
Слайд 4 После Фибоначчи осталось большое число задач. Мы с вами рассмотрим задачу
В итоге получается такая последовательность:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
Слайд 5 Числа Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
Свойства последовательности :
Каждое третье число Фибоначчи четное;
Каждое четвертое делится на три;
Каждое пятнадцатое оканчивается нулем;
Два соседних числа взаимно просты;
Слайд 61, 1, 2, 3, 5, 8, 13, . . .
Так отношение
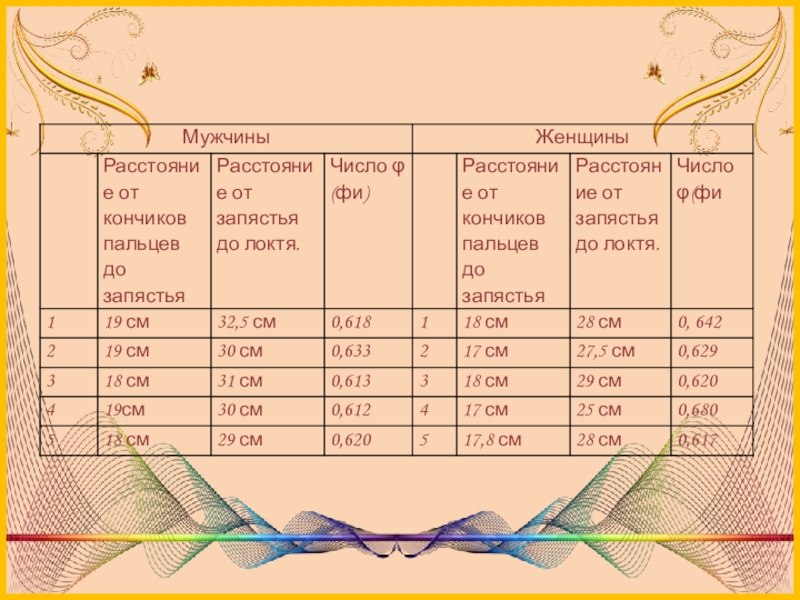
Слайд 7Если принять центром человеческого тела точку пупа, а расстояние между ступней
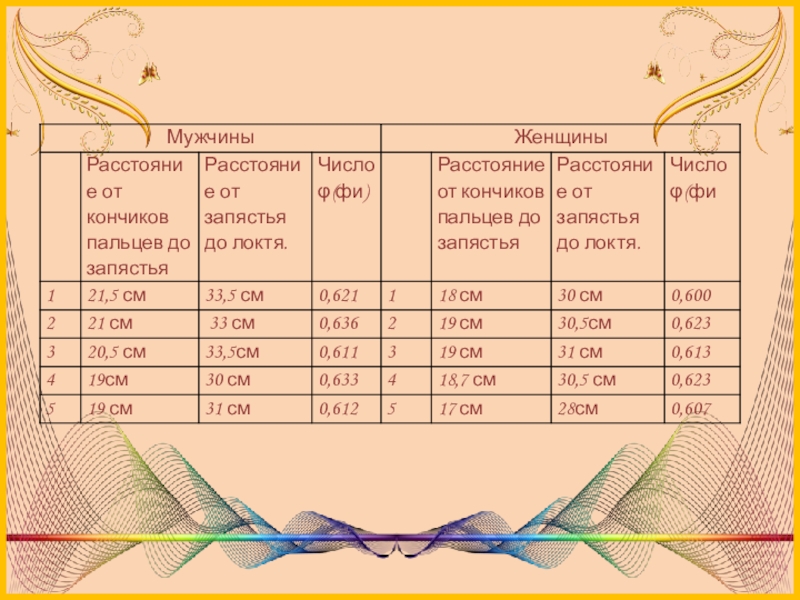
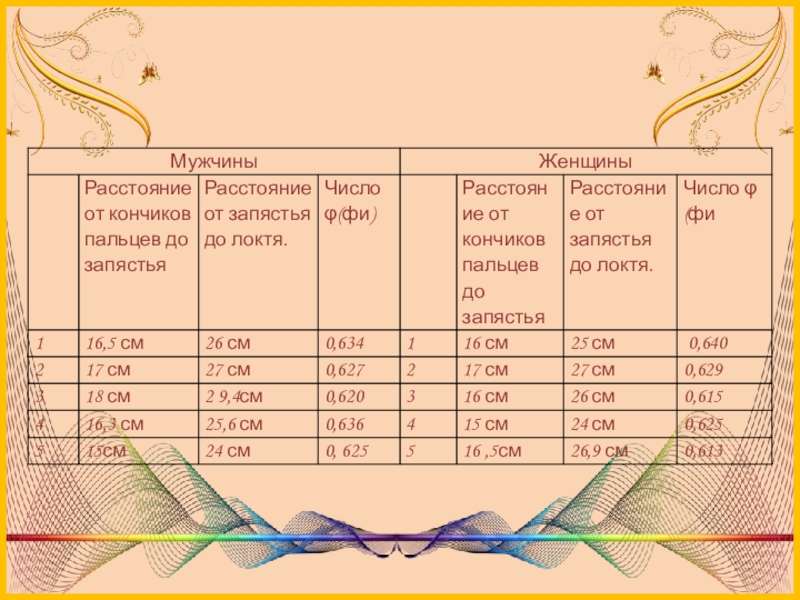
Расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1.618
Расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618
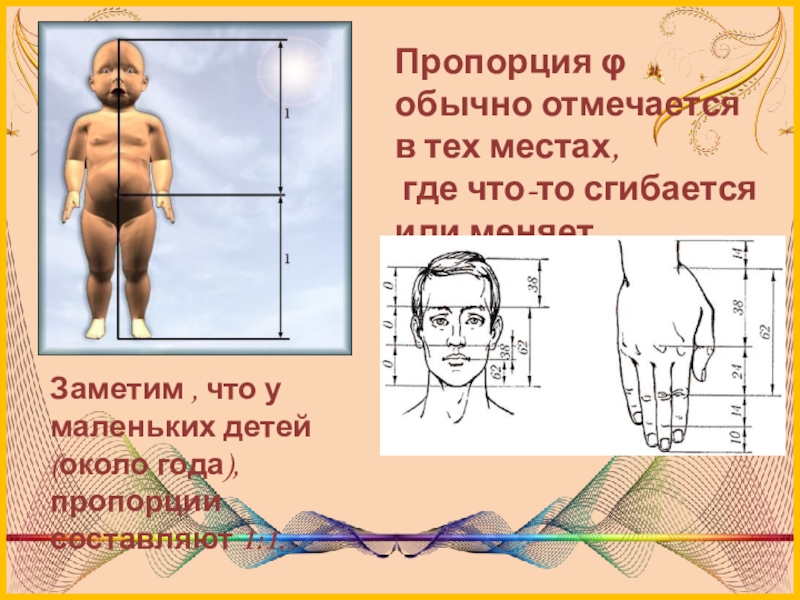
Слайд 8Пропорция φ обычно отмечается в тех местах,
где что-то сгибается или
Заметим , что у маленьких детей (около года), пропорции составляют 1:1.
Слайд 9
Рука человека.
У
Слайд 11
Числа Фибоначчи в живой природе.
Чёткая, симметричная форма цветов также подчинена
У многих цветов количество лепесточков – именно числа из ряда Фибоначчи. Например:
Ирис- 3 леп. Лютик -5 леп. Златоцвет-8 леп.
Слайд 13 Гипотеза.
Необычное явление, как числа Фибоначчи, не может не привлекать внимание.
Слайд 14Цели :
Изучить числовую последовательность Фибоначчи ;
Найти примеры использования чисел Фибоначчи в
Слайд 15Задачи:
Изучить литературу по данной теме. Описать числовой ряд Фибоначчи , коэффициент
Увидеть математические закономерности, в строении человека.
2. Провести измерения у людей длины кисти и предплечья.
3. Оформить результаты исследований в таблицах.
4. Выводы.
5. Заключение.
Слайд 16Астеническое телосложение
Астеническое телосложение подразумевает природную худобу и тонкость кости. Обычно у
Слайд 18
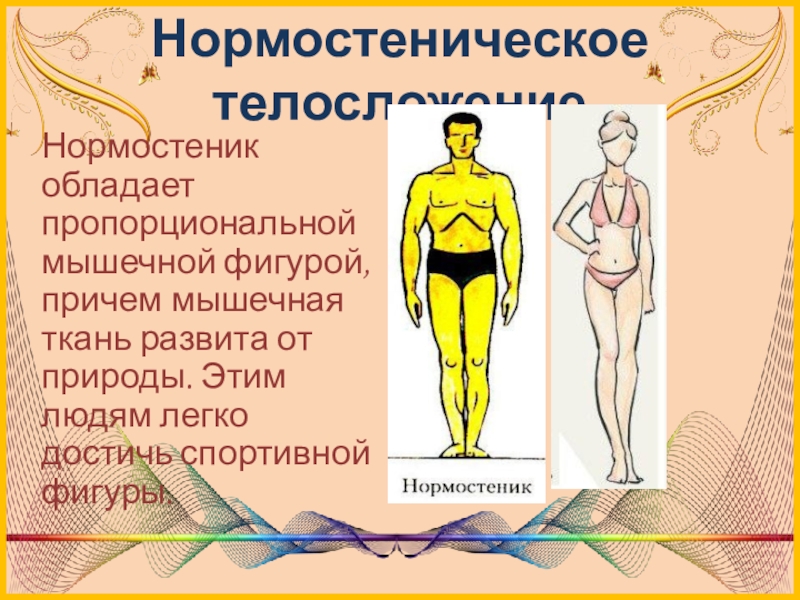
Нормостеническое телосложение
Нормостеник обладает пропорциональной мышечной фигурой, причем мышечная ткань развита от
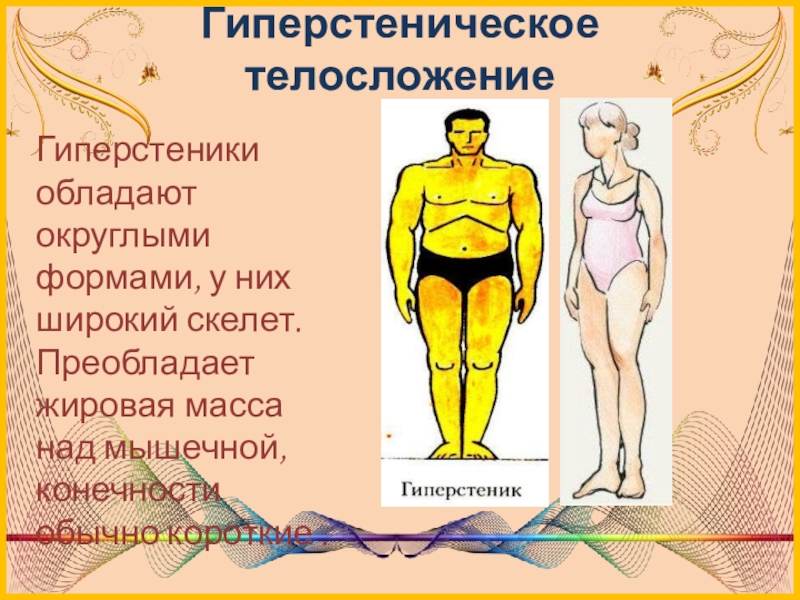
Слайд 20Гиперстеническое телосложение
Гиперстеники обладают округлыми формами, у них широкий скелет. Преобладает жировая
Слайд 22Выводы
Проанализировав результаты, представленные в таблицах, можно с уверенностью сказать, что наша
Слайд 23Заключение
Мы убедились, что у Природы есть свои законы, выраженные с помощью
В этой работе было показано, что в строении человека, окружающих нас растениях, живых организмах проявляют себя числа Фибоначчи и это отражает гармоничность их строения.
Работа отражает много интересного и познавательного. Например, теперь можно поискать числа Фибоначчи в окружающей нас природе.
Слайд 24Список литературы и сайтов.
1. Воробьев Н. Н. Числа Фибоначчи. – М.,
2. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три
взгляда на природу гармонии.-М., 1990.
3. http://www.tutoronline.ru/blog/chisla-fibonachchi-ishhem-sekret-mirozdanija
4. http://x-uni.com/referat/221823
5. http://revolution.allbest.ru/mathematics/00258246_0.html
6. https://ru.wikipedia.org/wiki/Числа_Фибоначчи
7. http://investments.academic.ru/1499/Фибоначчи
8. http://vestnik-nou.narod.ru/solotoe_sechenie.htm