- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по инженерной графике на тему Основные положения начертательной геометрии. Проекции точки
Содержание
- 1. Презентация по инженерной графике на тему Основные положения начертательной геометрии. Проекции точки
- 2. Раздел : Основы начертательной геометрии
- 3. Тема: Основные положения начертательной геометрии. Проекции точкиПланИсторическая
- 4. Выполнение чертежей зданий
- 5. Проектирование зданий
- 6. Дать правильный ответ Лист бумаги определенного размера
- 7. В своем классическом произведении
- 8. Начертательная геометрия является разделом геометрии, в котором
- 9. AVSCBS - центр проецирования,А, В,C - точки
- 10. sACBВ С А Метод в котором лучи
- 11. В А аІ вІ 3. ПРОЕКЦИЯ
- 12. Плоскости проекций делят пространство на 8 трехгранных
- 13. Слайд 13
- 14. Постоянная чертежаЧтобы получить ортогональные проекции точки на
- 15. V
- 16. Построение проекций точек
- 17. XYZYаIвIвIIаIIав651545903575В (45; 75; 65)А (90; 35; 15)Построить
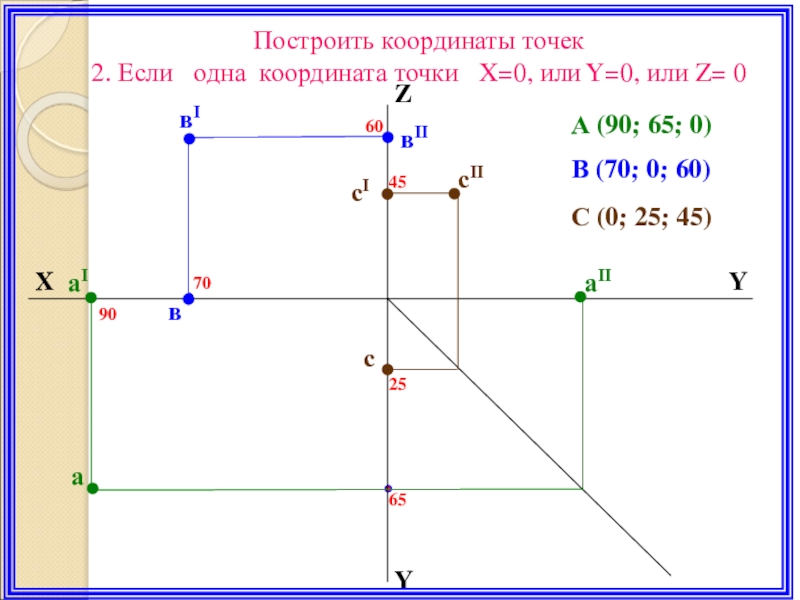
- 18. XYZYаIвIвIIаIIав60709065В (70; 0; 60)А (90; 65; 0)Построить
- 19. XYZYаIвIвIIаIIав5575В (0; 0; 55)А (75; 0; 0)С
- 20. ЧЧЕЕЕЕЕЕРРТТТТЖЖЯЯЗЗЫЫККККХХННИИИЕЕРТЖЯЗЫККХНИИЧЕТ- - - И
- 21. ЧЧЕЕЕЕЕЕРРТТТТЖЖЯЯЗЗЫЫККККХХННИИИЕЯЗЫККХНИИТ- - ИЕРТЖЧЕ-
Слайд 1предмет
Инженерная графика
Подготовил преподаватель
специалист 1 категории
ГПОУ «Макеевский политехнический колледж»
Крекова
Слайд 3Тема: Основные положения начертательной геометрии. Проекции точки
План
Историческая справка
Методы проецирования
Проекции точки
Д/З:
Выучить
2) Выполнить комплексные чертежи точек на формате А3
Боголюбов К.С. Индивидуальные задания по курсу черчение: задания №13,14,15
Слайд 6Дать правильный ответ
Лист бумаги определенного размера – это…
Чертежные инструменты -
Виды чертежных инструментов
Линия видимого контура - …
Какой линией выполняются надписи - …
Толщина линия видимого контуру равна - …
Толщина надписи равна - ...
Размер формата А4
Размер формата А3
Отношение линейного размера к действительному размеру - это …
Масштаб уменьшения - это...
Привести примеры масштаба уменьшения
Масштаб увеличения - это...
Привести примеры увеличение масштаба
Масштаб натуральная величина - это...
Слайд 7 В своем классическом произведении "Geometry descriptive" (Начертательная геометрия),
Начертательная геометрия, как научная дисциплина, возникла давно. В 1760-1770 годах выдающийся французский математик, геометр Гаспар Монж, рассматривал задачи о размещены укрепления в связи от расположения артиллерии противника, разработал основы начертательной геометри
1. ИСТОРИЧЕСКАЯ СПРАВКА
«Начертательная геометрия»
Основоположником начертательной геометрии и метода ортогонального проецирования является французский математик, геометр Гаспар Монж (1746-1818гг.).
Слайд 8Начертательная геометрия является разделом геометрии, в котором изучаются законы и методы
В начертательной геометрии чертеж выполняется с помощью метода проекций и называются проекционными чертежами.
Метод построения изображения геометрической формы на плоскости называется проецирование
Плоскость, на которую накладывается изображение от геометрической формы, называется плоскость проекций.
Линия пересечения двух плоскостей проекций называется ось проекций
Изображение которое строится на плоскости проекций с помощью метода проецирования называется проекция.
Линии, которые соединяют проекции на плоскостях называется линии связи.
Лучи, которые соединяют геометрическую форму и проекцию называется проецирующий луч
Чертеж (эпюр) точки, который состоит из двух трех ортогональных проекциях называется комплексным чертежом
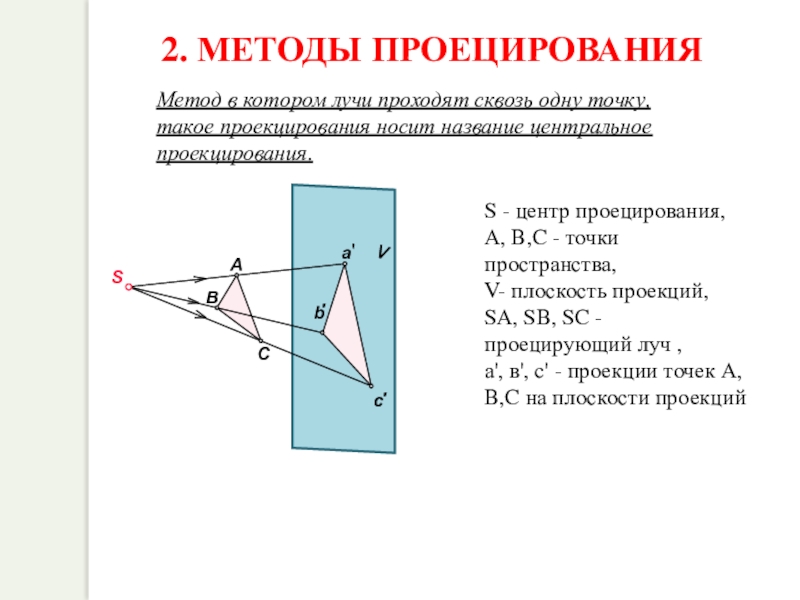
Слайд 9
A
V
S
C
B
S - центр проецирования,
А, В,C - точки пространства,
V- плоскость проекций,
SА, SВ,
а', в', c' - проекции точек А, В,C на плоскости проекций
2. МЕТОДЫ ПРОЕЦИРОВАНИЯ
Метод в котором лучи проходят сквозь одну точку, такое проекцирования носит название центральное проекцирования.
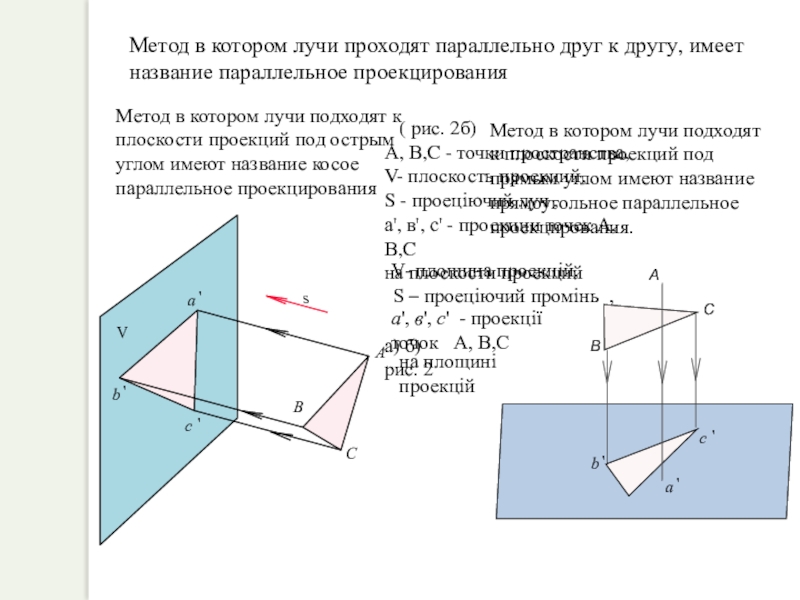
Слайд 10
s
A
C
B
В
С
А
Метод в котором лучи проходят параллельно друг к
Метод в котором лучи подходят к плоскости проекций под острым углом имеют название косое параллельное проекцирования
Метод в котором лучи подходят к плоскости проекций под прямым углом имеют название прямоугольное параллельное проекцирования.
( рис. 2б)
А, В,C - точки пространства,
V- плоскость проекций,
S - проеціючий луч ,
а', в', c' - проекции точек А, В,C
на плоскости проекций
а) б)
рис. 2
V- площина проекцій,
S – проеціючий промінь ,
а', в', c' - проекції
точок А, В,C
на площині проекцій
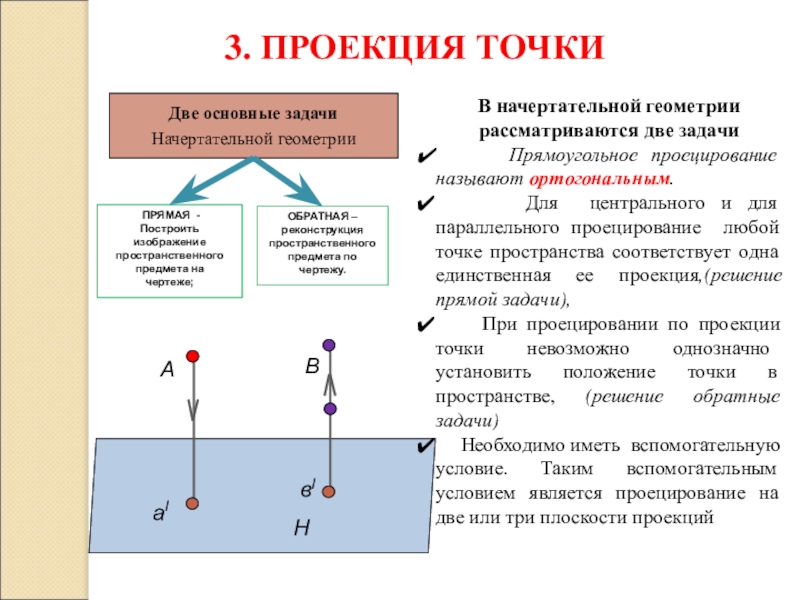
Слайд 11
В
А
аІ
вІ
3. ПРОЕКЦИЯ ТОЧКИ
В начертательной геометрии рассматриваются
Прямоугольное проецирование называют ортогональным.
Для центрального и для параллельного проецирование любой точке пространства соответствует одна единственная ее проекция,(решение прямой задачи),
При проецировании по проекции точки невозможно однозначно установить положение точки в пространстве, (решение обратные задачи)
Необходимо иметь вспомогательную условие. Таким вспомогательным условием является проецирование на две или три плоскости проекций
Две основные задачи
Начертательной геометрии
ПРЯМАЯ -
Построить
изображение
пространственного
предмета на
чертеже;
ОБРАТНАЯ –
реконструкция
пространственного
предмета по
чертежу.
H
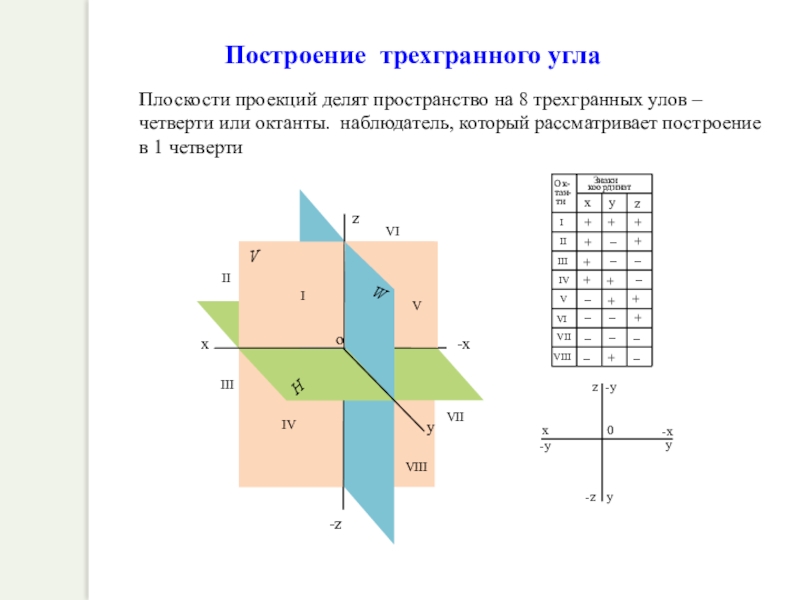
Слайд 12Плоскости проекций делят пространство на 8 трехгранных улов – четверти или
x
y
-x
-z
II
VI
VIII
V
I
VII
z
o
W
V
III
IV
H
Построение трехгранного угла
Слайд 13
V
W
900
900
х
у
H
z
у
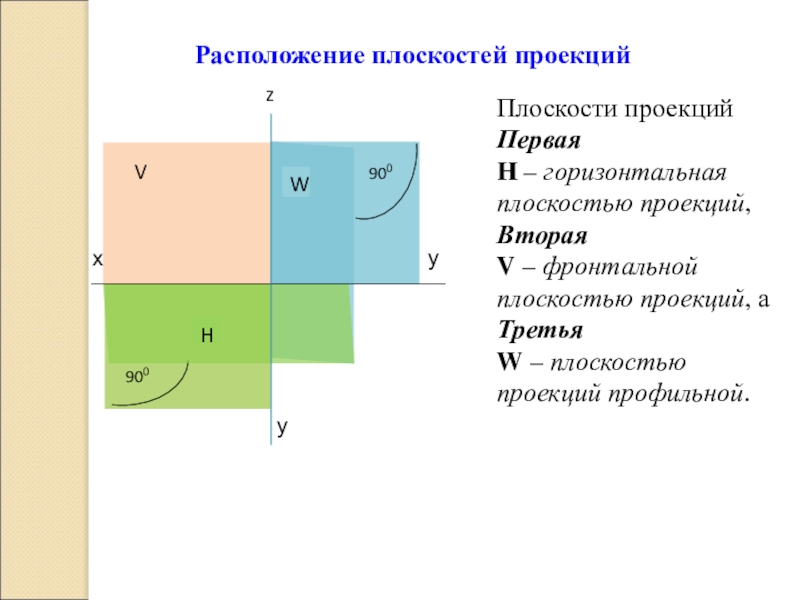
Плоскости проекций
Первая
H – горизонтальная плоскостью проекций,
Вторая
V – фронтальной плоскостью проекций, а
Третья
W – плоскостью проекций профильной.
Расположение плоскостей проекций
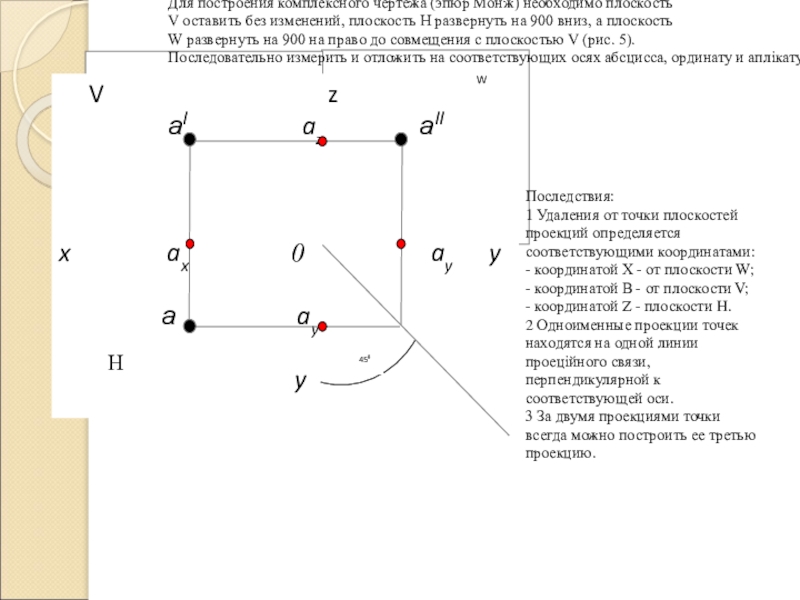
Слайд 14Постоянная чертежа
Чтобы получить ортогональные проекции точки на три взаимно-перпендикулярные плоскости проекций,
H - горизонтальная плоскость проекций;
V - фронтальная плоскость проекций;
W- профильная плоскость проекций;
О - начало координат;
Х, У, Z - оси проекции;
А - точка в пространстве;
а - горизонтальная,
аІ - фронтальная
аІІ - профильная проекции точки
V
W
х
у
H
z
у
Построение комплексного чертежа точки А
W
H
450
А
0
аІІ
аІ
а
аІІ
Слайд 15
V
аІ az аІІ
x ax 0 ay y
а ay
y
H
W
450
Последствия:
1 Удаления от точки плоскостей проекций определяется соответствующими координатами:
- координатой Х - от плоскости W;
- координатой В - от плоскости V;
- координатой Z - плоскости H.
2 Одноименные проекции точек находятся на одной линии проеційного связи, перпендикулярной к соответствующей оси.
3 За двумя проекциями точки всегда можно построить ее третью проекцию.
Проекции точки на три плоскости проекций
Для построения комплексного чертежа (эпюр Монж) необходимо плоскость
V оставить без изменений, плоскость H развернуть на 900 вниз, а плоскость
W развернуть на 900 на право до совмещения с плоскостью V (рис. 5).
Последовательно измерить и отложить на соответствующих осях абсцисса, ординату и аплікату точки А.
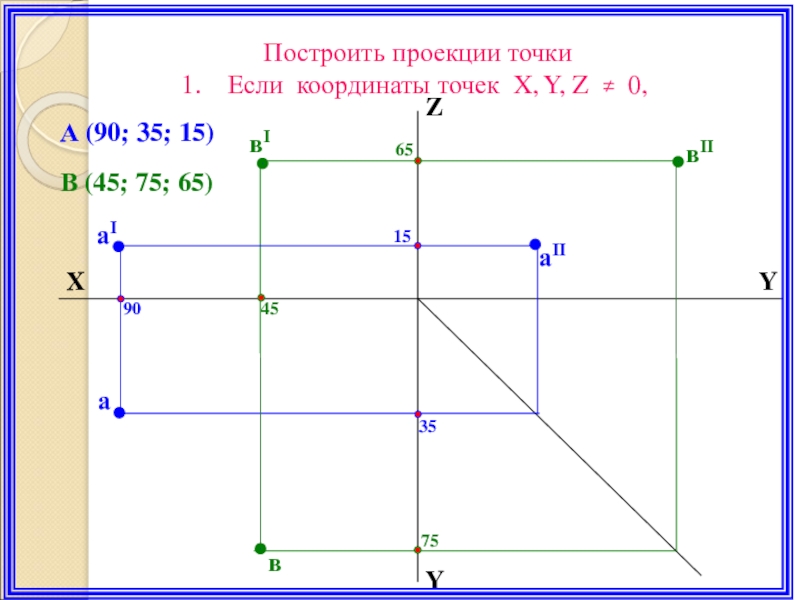
Слайд 17X
Y
Z
Y
аI
вI
вII
аII
а
в
65
15
45
90
35
75
В (45; 75; 65)
А (90; 35; 15)
Построить проекции точки
Если координаты точек
Слайд 18
X
Y
Z
Y
аI
вI
вII
аII
а
в
60
70
90
65
В (70; 0; 60)
А (90; 65; 0)
Построить координаты точек
2. Если
С (0; 25; 45)
25
45
сI
сII
с
Слайд 19X
Y
Z
Y
аI
вI
вII
аII
а
в
55
75
В (0; 0; 55)
А (75; 0; 0)
С (0; 30; 0)
30
с
сI
сII
Построить координаты
3. если две координаты точек: Y=Z=0, X=Z=0, X=Y=0