- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
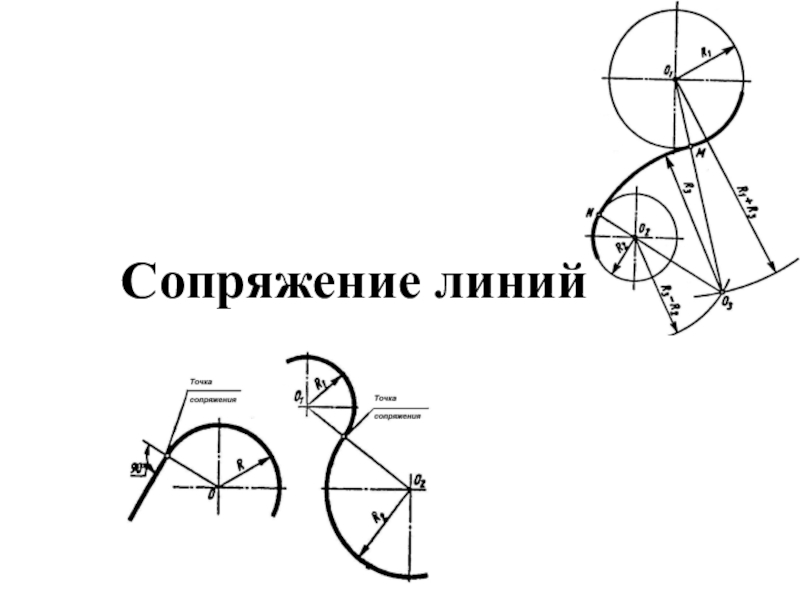
Презентация, доклад по инженерной графике на тему Сопряжение линий
Содержание
- 1. Презентация по инженерной графике на тему Сопряжение линий
- 2. Сопряжением называют плавный переход одной
- 3. Слайд 3
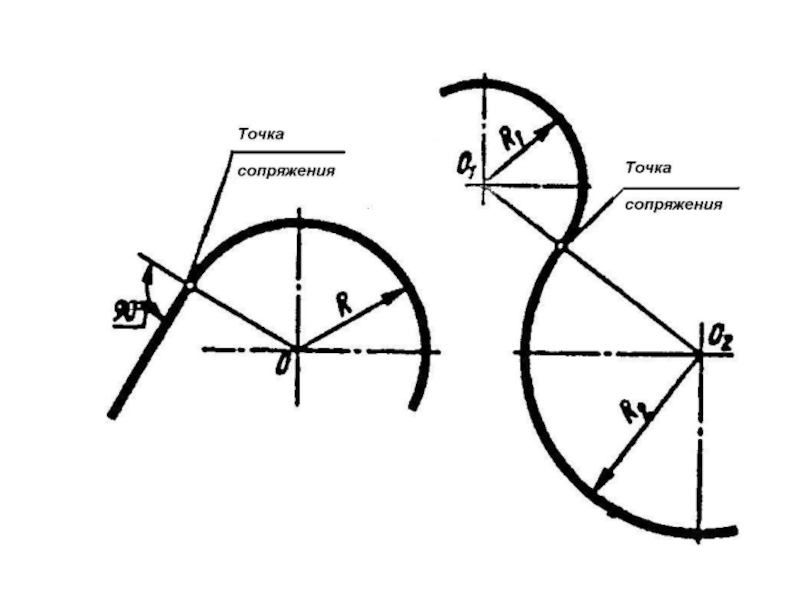
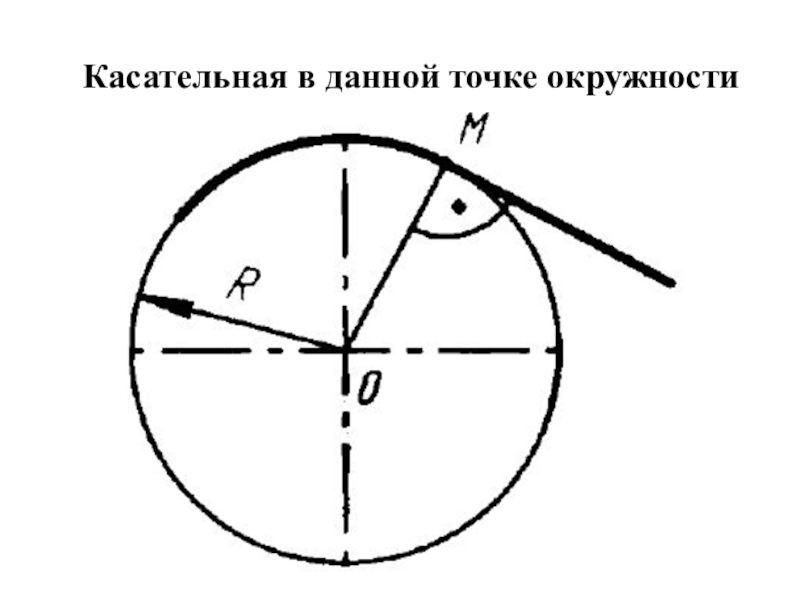
- 4. Касательная в данной точке окружности
- 5. Касательная к окружности из внешней точки
- 6. Сопряжение двух пересекающихся прямых дугой заданного радиуса
- 7. Слайд 7
- 8. Сопряжение двух параллельных прямых. Построение выполняют следующим
- 9. Слайд 9
- 10. Сопряжение дуги и прямой линии дугой заданного
- 11. 2. По общему правилу находят
- 12. Слайд 12
- 13. Кронштейн
- 14. Сопряжение дуги с прямой внутренним касанием
- 15. Маховик
- 16. Сопряжение дуги с дугойВнутреннее сопряжение.При внутреннем сопряжении
- 17. Внешнее сопряжение. При внешнем сопряжении центры О₁
- 18. Смешанное сопряжение дугПри смешанном сопряжении центр О2 одной
- 19. Слайд 19
- 20. Построение овала по заданному размеру большой оси овала АВ
- 21. 1. Ось АВ делим на три равные части
- 22. 2. Радиусом, равным расстоянию О1О2, из точек деления О1 и О2проводим окружности. Точки пересечения окружностей обозначаем как m и n.
- 23. 3. Соединяем точки m и n с точками О1 и О2 получаем прямые, которые продляем
- 24. 4. Из точек m и n, как из центров, радиусом Rmax,
- 25. Построение овала по двум заданным осям симметрииПроводят
- 26. Слайд 26
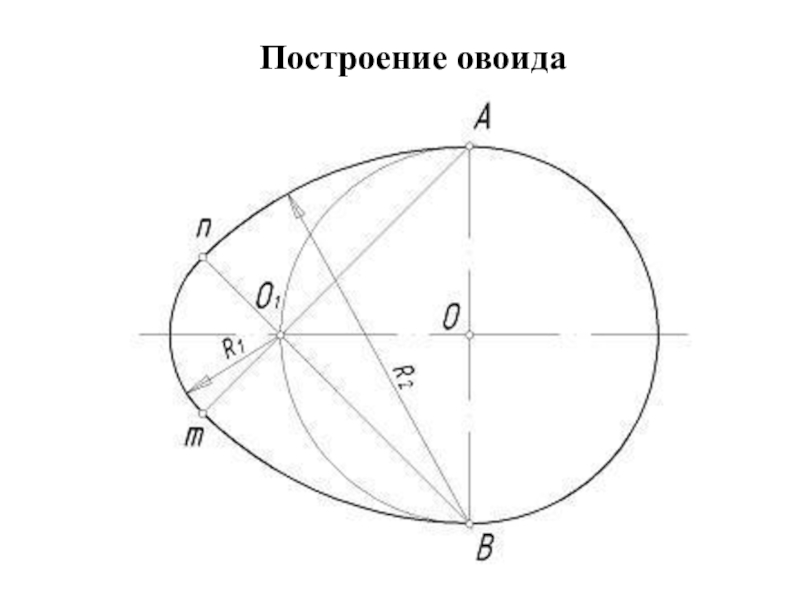
- 27. Построение овоида
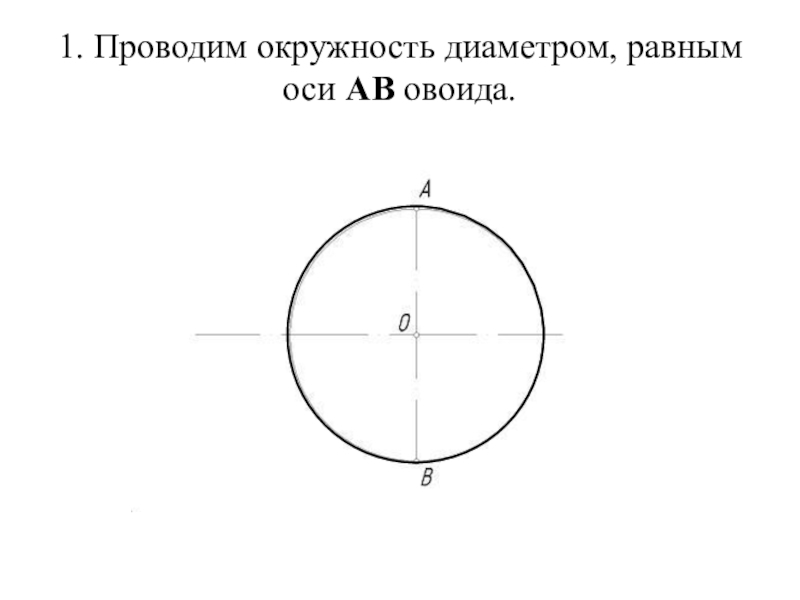
- 28. 1. Проводим окружность диаметром, равным оси АВ овоида.
- 29. 2. Из точек А и В через точку О1 (точка пересечения окружности с осью симметрии)проводят прямые.
- 30. 3. Из точек А и В, как из центров, радиусом R2, равным расстоянию АВ, проводим дуги Аn и Вm.
- 31. 4. Из центра О1 радиусом R1=О1n проводим малую дугу овоида mn.
- 32. Построение завиткаПоследовательность построения завиткаВычерчивается в тонких линиях
- 33. Слайд 33
Сопряжением называют плавный переход одной линии (прямой или кривой) в другую – кривую или прямую. Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений. Затем
Слайд 2
Сопряжением называют плавный переход одной линии (прямой или кривой)
в другую – кривую или прямую.
Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений. Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений.
Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений. Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений.
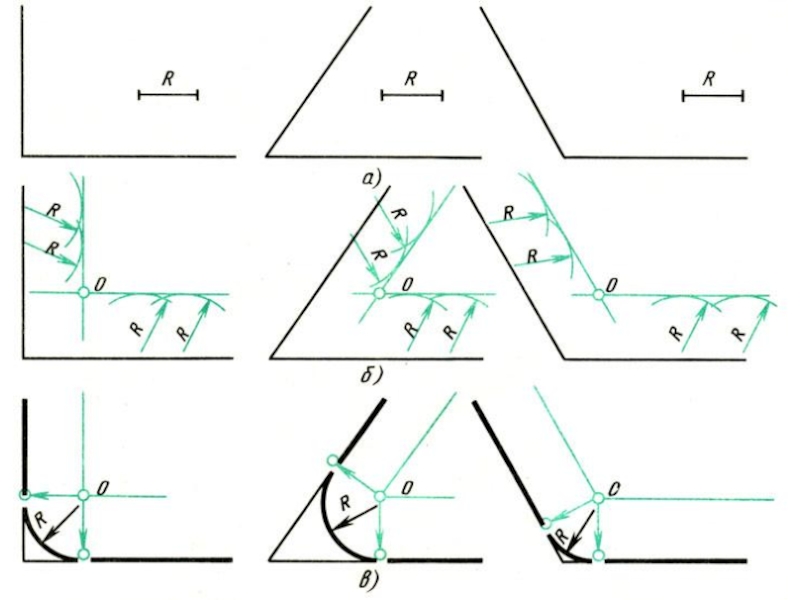
Слайд 6Сопряжение двух пересекающихся прямых дугой заданного радиуса R.
1. Находят
точку О - центр сопряжения, который должен лежать на расстоянии R от сторон угла в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них.
Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.
2. Находят точки сопряжений. Для этого опускают перпендикуляры из точки О на заданные прямые.
3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений.
Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.
2. Находят точки сопряжений. Для этого опускают перпендикуляры из точки О на заданные прямые.
3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений.
Слайд 8Сопряжение двух параллельных прямых.
Построение выполняют следующим образом:
1. Находят центр
сопряжения и радиус дуги. Для этого из точки m на одной прямой восставляют перпендикуляр до пересечения с другой прямой в точке n. Отрезок делят пополам
2. Из точки О - центра сопряжения радиусом
Оm = Оn описывают дугу до точек сопряжения m и n
2. Из точки О - центра сопряжения радиусом
Оm = Оn описывают дугу до точек сопряжения m и n
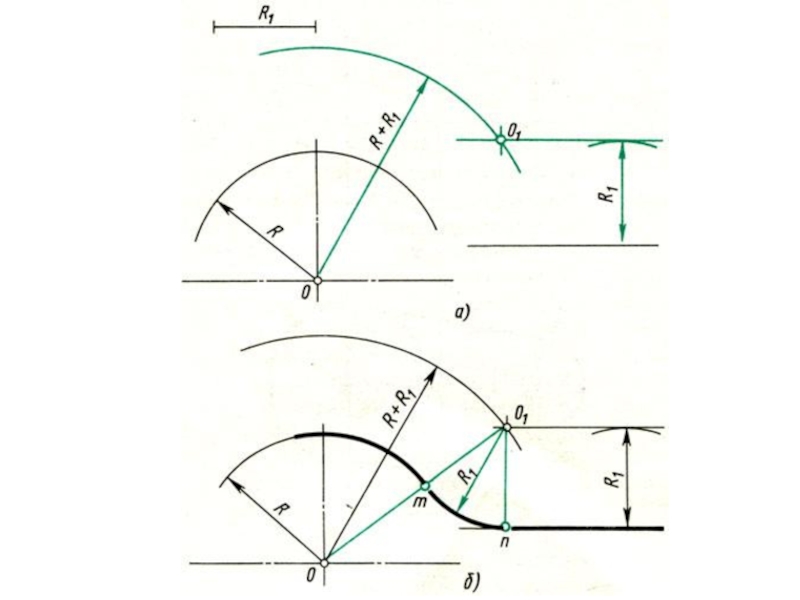
Слайд 10Сопряжение дуги и прямой линии дугой заданного радиуса.
Заданы дуга окружности радиусом
R и прямая. Требуется соединить их дугой радиусом R1.
1. Находят центр сопряжения, который должен находиться на расстоянии R1 от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R1, и вспомогательной дуги, отстоящей от заданной также на расстоянии R1. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R1 Раствором циркуля, равным сумме заданных радиусов R + R1, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O1- центр сопряжения.
1. Находят центр сопряжения, который должен находиться на расстоянии R1 от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R1, и вспомогательной дуги, отстоящей от заданной также на расстоянии R1. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R1 Раствором циркуля, равным сумме заданных радиусов R + R1, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O1- центр сопряжения.
Слайд 11 2. По общему правилу находят точки сопряжения. Соединяют прямой
центры сопрягаемых дуг O1 и О. Опускают из центра сопряжения O1 перпендикуляр на заданную прямую.
3. Из центра сопряжения O1 между точками сопряжения m и n проводят дугу, радиус которой равен R1
3. Из центра сопряжения O1 между точками сопряжения m и n проводят дугу, радиус которой равен R1
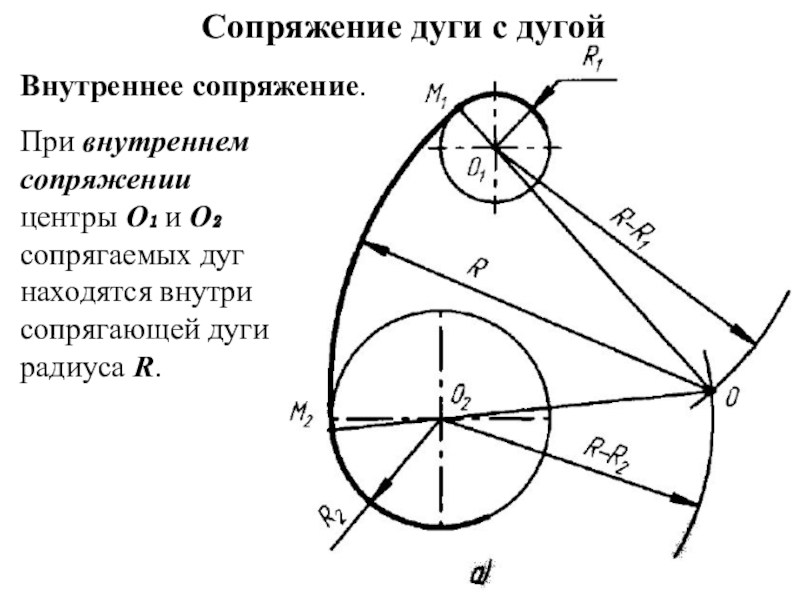
Слайд 16Сопряжение дуги с дугой
Внутреннее сопряжение.
При внутреннем сопряжении
центры О₁ и О₂ сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R.
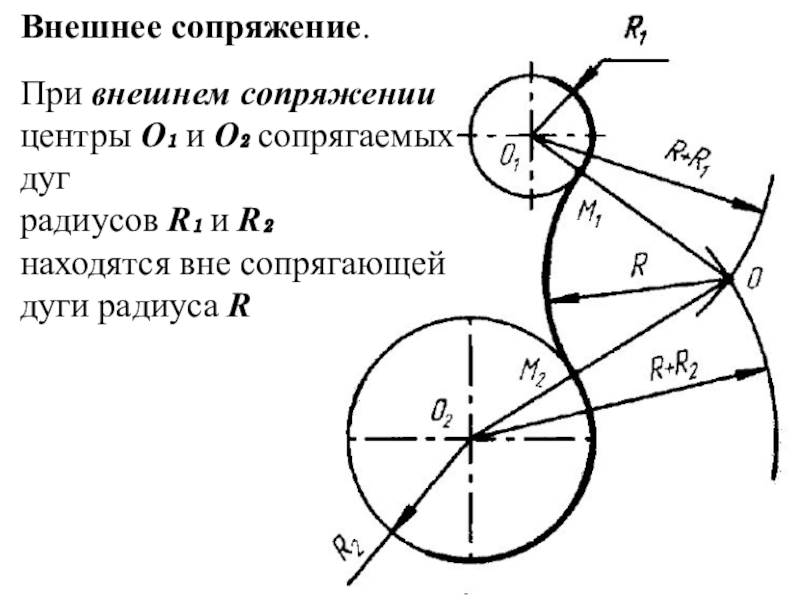
Слайд 17Внешнее сопряжение.
При внешнем сопряжении центры О₁ и О₂ сопрягаемых дуг
радиусов R₁ и R₂
находятся вне сопрягающей дуги радиуса R
Слайд 18Смешанное сопряжение дуг
При смешанном сопряжении центр О2 одной из сопрягаемых дуг лежит
внутри сопрягающей дуги радиуса R, а центр О1 другой сопрягаемой дуги вне ее.
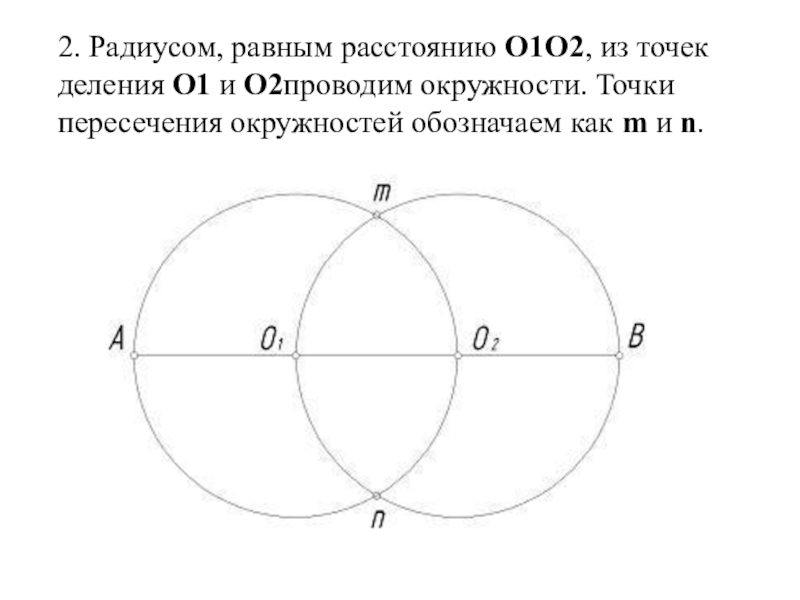
Слайд 222. Радиусом, равным расстоянию О1О2, из точек деления О1 и О2проводим окружности. Точки пересечения окружностей
обозначаем как m и n.
Слайд 233. Соединяем точки m и n с точками О1 и О2 получаем прямые, которые продляем до пересечения с окружностями.
Полученные точки (1,2,3 и 4) являются точками сопряжениями дуг.
Слайд 244. Из точек m и n, как из центров, радиусом Rmax, равным n 2 и m 3, проводим
верхнюю дугу 1 2 и нижнюю дугу 3 4.
Слайд 25Построение овала по двум заданным осям симметрии
Проводят оси АВ и CD.
Из точки их пересечения радиусом ОС проводят дугу до пересечения с большой осью овала АВ в точке N. Точку А соединяют прямой с точкой С и на ней от точки С откладывают отрезок NB, получают точку N₁. В середине отрезка AN₁ восстанавливают перпендикуляр и продолжают его до пересечения с большой и малой осями овала в точках O₁ и n. Расстояние ОО₁ откладывают по большой оси овала вправо от точки О, а расстояние Оn от точки О откладывают по малой оси овала вверх, получают точки n₁ и O₂. Точки n и n₁ являются центрами верхней дуги 12 и нижней дуги 34 овала, точки О₁ и O₂ - центрами дуг 13 и 24. Получают искомый овал.
Слайд 292. Из точек А и В через точку О1 (точка пересечения окружности с осью симметрии)проводят прямые.
Слайд 303. Из точек А и В, как из центров, радиусом R2, равным расстоянию АВ, проводим дуги Аn и Вm.
Слайд 32Построение завитка
Последовательность построения завитка
Вычерчивается в тонких линиях контур «глазка», окружность с
диаметром О₁О₂. Из точек О₁ и О₂, как из центров, проводят две сопряженные между собой полуокружности. Верхние полуокружности из центра О₁, нижние полуокружности из центра О₂. Получаем искомый завиток.
Глазок имеет форму правильного треугольника ОО₁О₂. Стороны треугольника продолжают. Приняв за центры сопряжения вершины треугольника «глазка», проводят в направлении движения часовой стрелки ряд сопряженных между собой дуг. Центром первой дуги является точка О, центр второй - О₁…
Глазок имеет форму правильного треугольника ОО₁О₂. Стороны треугольника продолжают. Приняв за центры сопряжения вершины треугольника «глазка», проводят в направлении движения часовой стрелки ряд сопряженных между собой дуг. Центром первой дуги является точка О, центр второй - О₁…