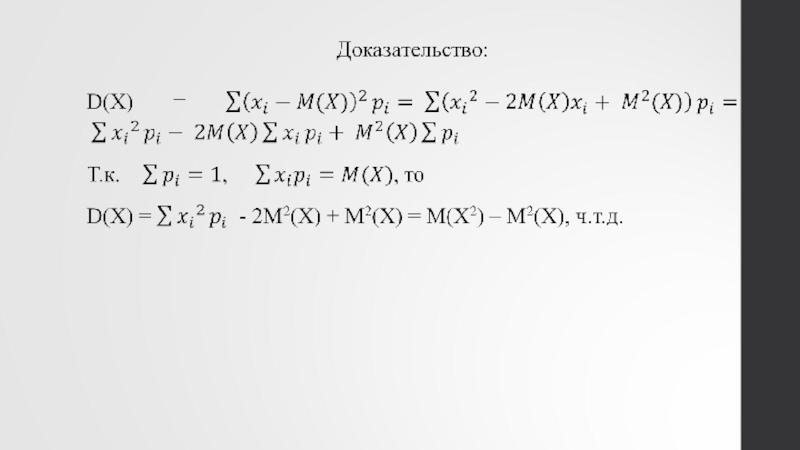- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Теория вероятностей и математическая статистика на тему Числовые характеристики ДСВ
Содержание
- 1. Презентация по дисциплине Теория вероятностей и математическая статистика на тему Числовые характеристики ДСВ
- 2. 1. Мода и медиана ДСВМодой ДСВ называется
- 3. 1. Мода и медиана ДСВМедианой ДСВ называется
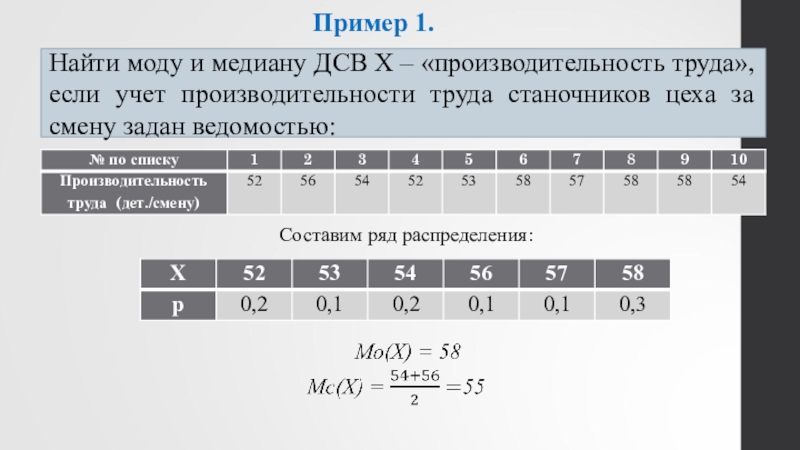
- 4. Пример 1.Найти моду и медиану ДСВ Х
- 5. 2. Математическое ожидание
- 6. 1. Математическое ожидание(!!) Математическое ожидание называют еще
- 7. Пример 2.Найти математическое ожидание случайной величины Х, имеющей следующий закон распределения:М(Х) = 0,3+0,4+0,3+0,8+1 = 2,8
- 8. Пример 3.Из 100 лотерейных билетов в тридцати
- 9. Свойства математического ожиданияСвойство 1. Математическое ожидание постоянной
- 10. Свойства математического ожиданияСвойство 4. Математическое ожидание суммы
- 11. Пример 4.Найти математическое ожидание случайной величины Х·У,
- 12. Пример 5.Найти математическое ожидание суммы числа очков,
- 13. Пусть даны законы распределения ДСВ Х и
- 14. 3. Дисперсия СВДисперсией СВ называется математическое ожидание
- 15. 3. Дисперсия СВ
- 16.
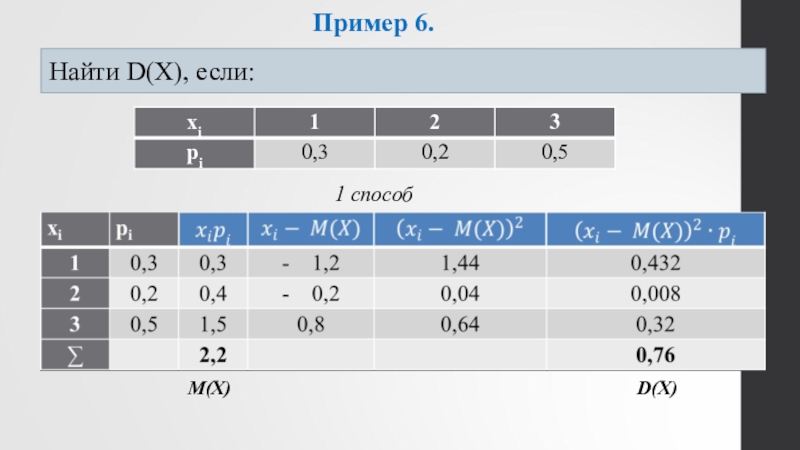
- 17. Пример 6.Найти D(X), если:1 способ М(Х)
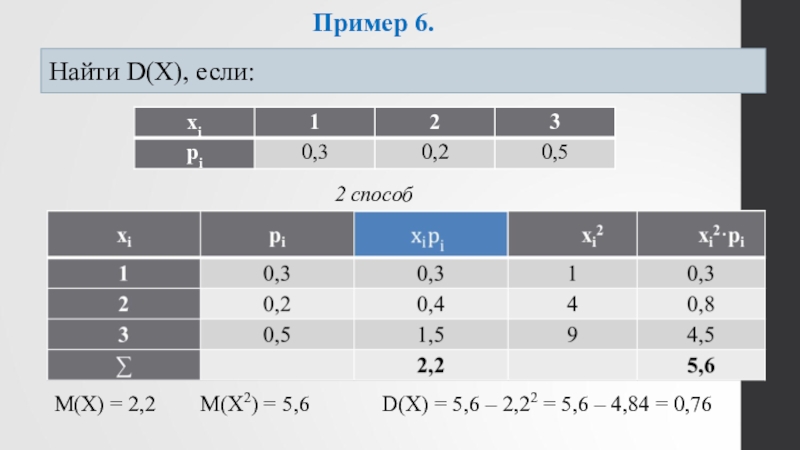
- 18. Пример 6.Найти D(X), если:2 способM(X) = 2,2
- 19. Пример 7.Сравнить дисперсии СВ, заданных законами распределения:
- 20. Свойства дисперсии
- 21. Пример 8.Дисперсия СВ Х равна 5. Найти
- 22. 4. Среднеквадратичное отклонение
- 23. Пример 9.Найти М(Х), D(X) и σ(Х), если
Слайд 1
Числовые характеристики дискретных случайных величин
Беляева Татьяна Юрьевна
ГБПОУ КК «Армавирский машиностроительный техникум»
Преподаватель
Слайд 21. Мода и медиана ДСВ
Модой ДСВ называется такое ее значение, вероятность
Обозначение: Мо(Х)
(!!) Ряд распределений может не иметь моды или иметь не одну, а несколько мод.
Слайд 31. Мода и медиана ДСВ
Медианой ДСВ называется среднее по положению в
Обозначение: Мс(Х)
(!!) В ряду с нечетным количеством членов медиана есть значение ДСВ на «среднем месте». Если в ряду распределения четное число членов, то медиана вычисляется как среднее арифметическое двух значений, стоящих в середине ряда.
Слайд 4Пример 1.
Найти моду и медиану ДСВ Х – «производительность труда», если
Составим ряд распределения:
Слайд 61. Математическое ожидание
(!!) Математическое ожидание называют еще средним значением СВ или
(!!) Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.
Слайд 7Пример 2.
Найти математическое ожидание случайной величины Х, имеющей следующий закон распределения:
М(Х)
Слайд 8Пример 3.
Из 100 лотерейных билетов в тридцати выигрыш составляет 100 тыс.
Мо(Х) = 0
Мс(Х) = 200 тыс.
М(Х) = … = 75 тыс.
Составим ряд распределения СВ Х – «сумма выигрыша»:
Слайд 9Свойства математического ожидания
Свойство 1. Математическое ожидание постоянной величины равно этой постоянной:
М(С) = С.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
М(С·Х) = С·М(Х).
Свойство 3. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей:
М(Х·У) = М(Х) · М(У)
Слайд 10Свойства математического ожидания
Свойство 4. Математическое ожидание суммы случайных величин равно сумме
Свойство 5. Математическое ожидание отклонения случайной величины Х от ее математического ожидания М(Х) равно нулю:
М(Х – М(Х)) = 0
Математическое ожидание M(X) – вполне определенная постоянная. В результате опыта СВ Х принимает одно из ее возможных значений хi. Разность хi – M(X) показывает, насколько отклонилось это значение СВ в данном опыте от М(Х). Очевидно, что эта разность сама является случайной величиной. Эту величину обозначают Х – М(Х) и называют отклонением случайной величины Х от ее математического ожидания.
Слайд 11Пример 4.
Найти математическое ожидание случайной величины Х·У, если независимые случайные величины
М(Х) = 0,2 + 1,2 + 3 = 4,4
М(У) = 5,6 + 1,8 = 7,4
М(ХУ) = 4,4 · 7,4 = 32,56
Слайд 12Пример 5.
Найти математическое ожидание суммы числа очков, которые могут выпасть при
М(Х) = 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3,5
М(У) = 3,5
М(Х + У) = 3,5 + 3,5 = 7
Слайд 13Пусть даны законы распределения ДСВ Х и У:
Математические ожидания обеих
Слайд 143. Дисперсия СВ
Дисперсией СВ называется математическое ожидание квадрата отклонения СВ от
Обозначение: D(Х)
D(X) = M (X – M(X))2
Слайд 18Пример 6.
Найти D(X), если:
2 способ
M(X) = 2,2 M(X2)
Слайд 21Пример 8.
Дисперсия СВ Х равна 5. Найти дисперсию следующих величин:
А) Х
Б) -2Х
В) 3Х + 6
А) 5
В) 20
С) 45
Слайд 23Пример 9.
Найти М(Х), D(X) и σ(Х), если СВ задана следующим рядом
(!!) Для удобства вычислений все результаты можно свести в таблицу. При этом вид таблицы зависит от способа вычисления дисперсии.
Можно также все выкладки производить в строчку, без составления таблиц.