- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций
Содержание
- 1. Презентация по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций
- 2. Аппроксимация, интерполяция, экстраполяция Аппроксимация (приближение) функции f(x)
- 3. ИнтерполяцияИнтерполяция имеет как практическое, так и теоретическое
- 4. Задача интерполяцииПусть функция f(x) задана таблицей своих
- 5. Глобальная интерполяцияФункция f(x) интерполируется на всем интервале
- 6. Интерполяция полиномомФактически задача сводится к определению коэффициентов
- 7. Визуализация интерполируемой функции в MATLABДля примера возьмем исходную функцию Построим график данной функции:>> x=linspace(2,7,1000);>> y=sin(2.*x).*sin(x);>> plot(x,y)
- 8. Интерполяция полиномом: постановка задачиПусть заданы узлы интерполяции:
- 9. Интерполяция полиномом: расчет коэффициентов матричным методомСистема уравнений
- 10. Блок-схема программы интерполяции полиномом
- 11. Расчет коэффициентов полинома матричным методом в MATLABРешаем
- 12. Значения коэффициентов полиномаA =
- 13. Расчет промежуточных значений функции в MATLAB при
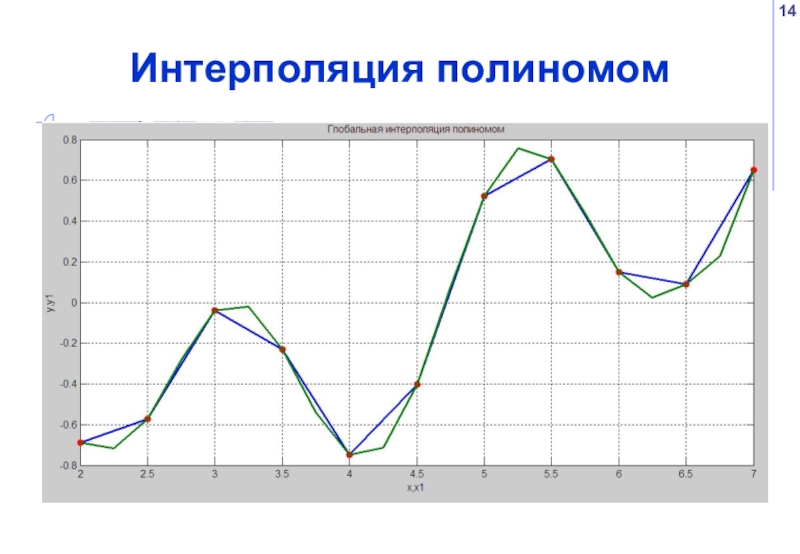
- 14. Интерполяция полиномом
- 15. Глобальная или локальная?Пример:>> x=2:0.25:15; % задаем узловые
- 16. Линейная интерполяция Узловые точки соединяются отрезками
- 17. Локальная интерполяция функции в MATLABДля одномерной табличной
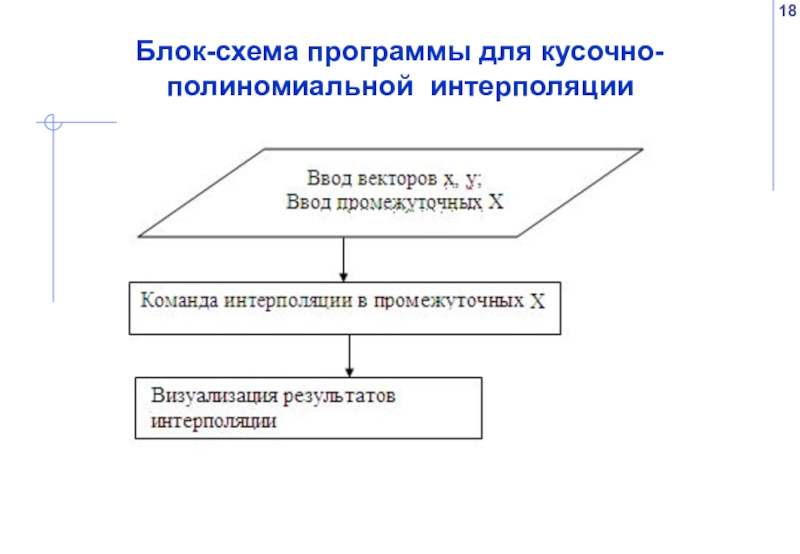
- 18. Блок-схема программы для кусочно-полиномиальной интерполяции
- 19. Ступенчатая интерполяция и ее визуализация в MATLABИспользуем
- 20. Линейная интерполяция и ее визуализация в MATLAB>>
- 21. Интерполяция кубическими сплайнами и ее визуализация в
- 22. Интерполяция многочленами Эрмитами ее визуализация в MATLAB>>
- 23. Сравнение погрешностей методов интерполяции функции yi=sin(2*X).*sin(X) в MATLABФайл-функция для определения погрешности:function p=pogr(X,Y);yi=sin(2.*X).*sin(X);P=abs(yi-Y);p=P;max (p)end
- 24. Погрешность ступенчатой интерполяции:>> X=linspace(2,7,51);>> Y=interp1(x,y,X,'nearest');>> p=pogr(X,Y)ans = 0.3752
- 25. Погрешность линейной интерполяции:>> X=linspace(2,7,51);>> Y1=interp1(x,y,X,'linear');>> p1=pogr(X,Y1)ans = 0.1400
- 26. Погрешность интерполяции кубическими сплайнами:>> X=linspace(2,7,51);>> Y2=interp1(x,y,X,'spline');>> p2=pogr(X,Y2)ans = 0.0545
- 27. Погрешность интерполяции многочленами Эрмита:>> X=linspace(2,7,51);>> Y3=interp1(x,y,X,'cubic');>> p3=pogr(X,Y3)ans = 0.1046Вывод: наименьшую погрешность дает интерполяция кубическими сплайнами
- 28. Аппроксимация функцийАппроксимацией (приближением) функции f(x) называется нахождение
- 29. Аппроксимация функций в MATLABОдна из наиболее известных
- 30. Аппроксимация функции y=sin(2x)·sin(x) полиномами>> x=2:0.5:7;>> y=sin(2.*x).*sin(x);>> p=polyfit(x,y,3)
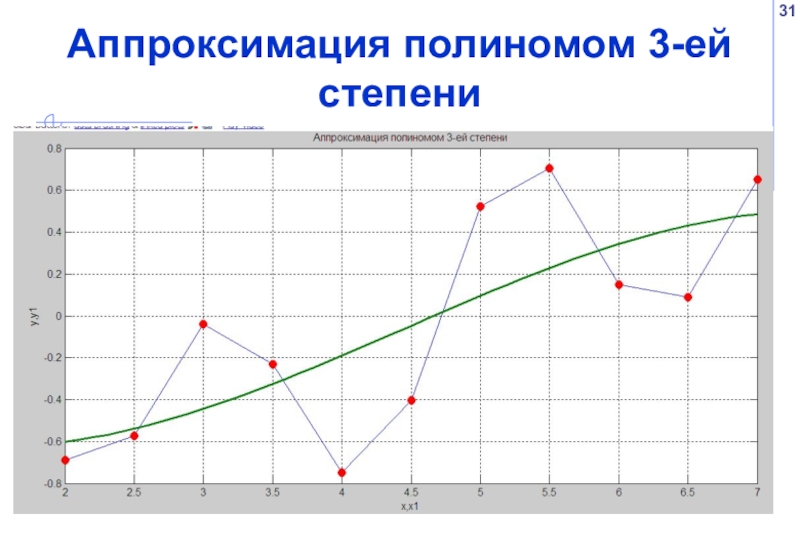
- 31. Аппроксимация полиномом 3-ей степени
- 32. Аппроксимация полиномом 5-й степени>> p1=polyfit(x,y,5) % аппроксимация
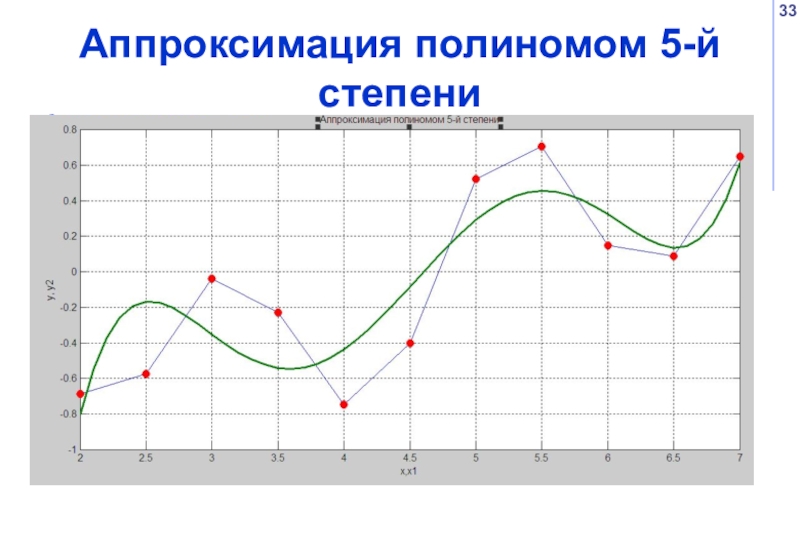
- 33. Аппроксимация полиномом 5-й степени
- 34. Аппроксимация полиномом 7-й степени
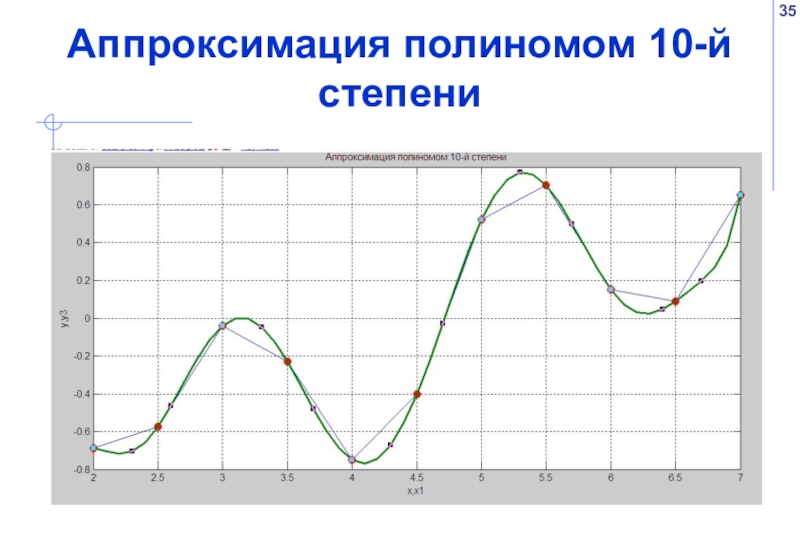
- 35. Аппроксимация полиномом 10-й степени
- 36. Влияние степени полинома на вид приближающей функцииПри
- 37. Аппроксимация полиномом 20-й степени
- 38. Метод наименьших квадратовДля оценки «близости» функций выбирают
- 39. Нахождение приближающей функции в виде линейной функции
- 40. Нахождение приближающей функции в виде линейной функции
- 41. Система уравненийМх, Мх2, Мхy – коэффициенты уравнений, определяемые по формулам:
- 42. ЗадачаВ одной системе координат построить графики табличной
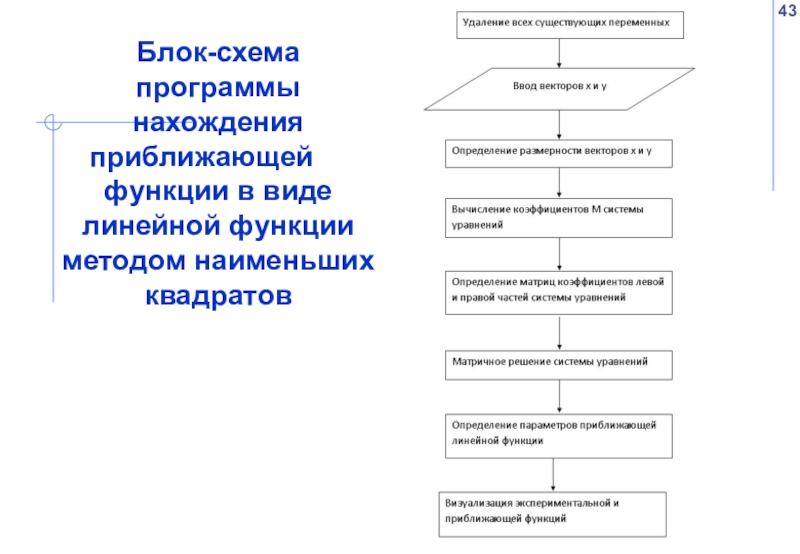
- 43. Блок-схема программы нахождения приближающей функции в виде линейной функции методом наименьших квадратов
- 44. Программа для нахождения приближающей функции в виде
- 45. Нахождение приближающей функции в виде линейной функции
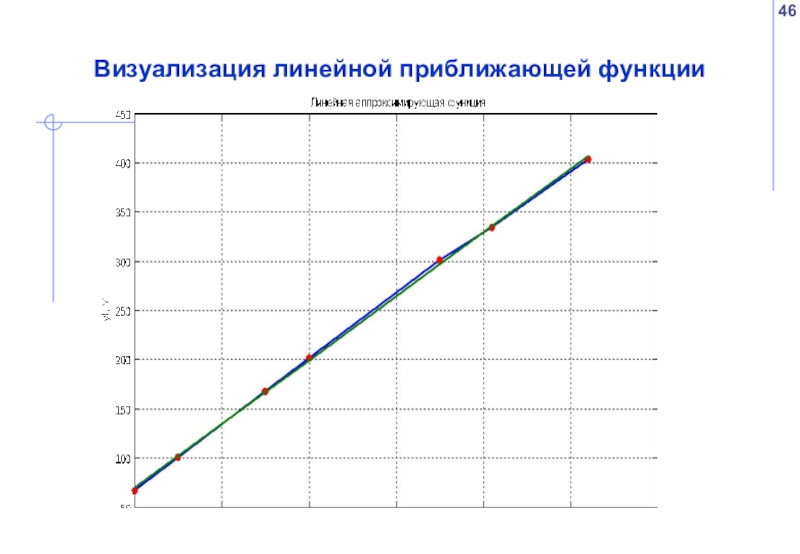
- 46. Визуализация линейной приближающей функции
- 47. Путем построения кубического сплайна с помощью стандартной
- 48. Решение задачи 1>> t=50:50:200;>> E=[0.299 0.645 1.029 1.44];>> t1=180;>> E1=interp1(t,E,t1,'spline')E1 = 1.2731
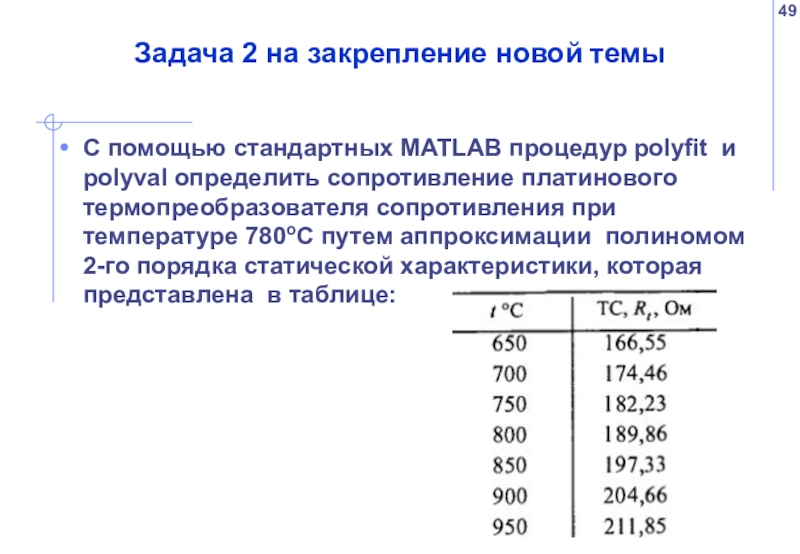
- 49. С помощью стандартных MATLAB процедур polyfit и
- 50. >> t=650:50:950;>> R=[166.55 174.46 182.23 189.86 197.33
Слайд 1Тема занятия Численные методы интерполяции и аппроксимации функции. Интерполяция и аппроксимация
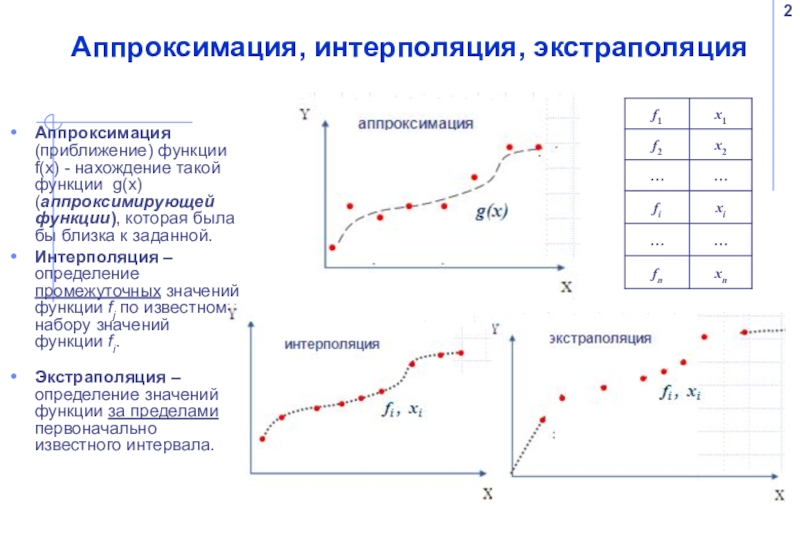
Слайд 2Аппроксимация, интерполяция, экстраполяция
Аппроксимация (приближение) функции f(x) - нахождение такой функции
Интерполяция – определение промежуточных значений функции fj по известному набору значений функции fi.
Экстраполяция – определение значений функции за пределами первоначально известного интервала.
Слайд 3Интерполяция
Интерполяция имеет как практическое, так и теоретическое значение. На практике часто
Слайд 4Задача интерполяции
Пусть функция f(x) задана таблицей своих значений xi, yi: на
Задача интерполяции - найти функцию g(x), принимающую в точках xi те же значения yi
точки xi – узлы интерполяции
условие g(x)= yi – условие интерполяции
Через заданные точки можно провести бесконечно много кривых, для каждой из которых выполнены все условия интерполяции.
Слайд 5Глобальная интерполяция
Функция f(x) интерполируется на всем интервале [a; b] обычно с
Если количество узловых точек равно n, то степень полинома равна n-1, т.е. на единицу меньше количества узлов интерполяции.
Слайд 6Интерполяция полиномом
Фактически задача сводится к определению коэффициентов интерполяционного полинома на основании
Существуют различные численные методы решения данной задачи.
В пакете MATLAB имеются специальные функции для построения интерполяционного полинома.
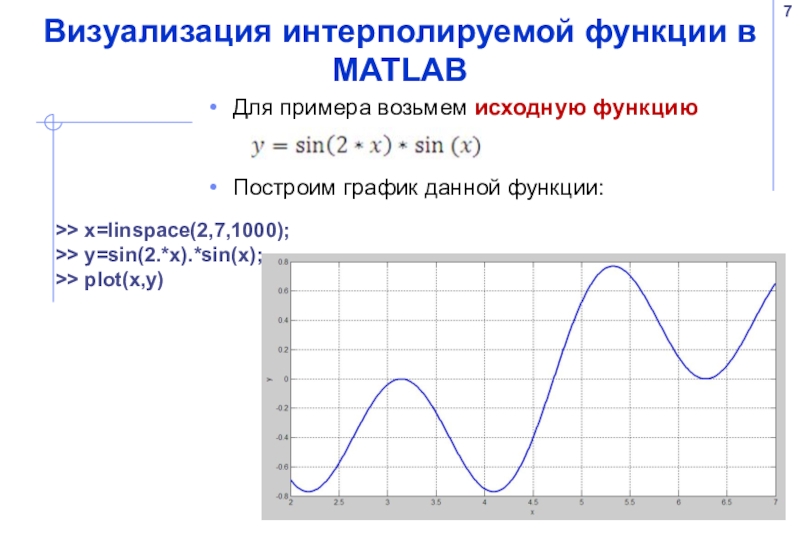
Слайд 7Визуализация интерполируемой функции в MATLAB
Для примера возьмем исходную функцию
Построим график
>> x=linspace(2,7,1000);
>> y=sin(2.*x).*sin(x);
>> plot(x,y)
Слайд 8Интерполяция полиномом: постановка задачи
Пусть заданы узлы интерполяции:
xнач=2; xконечн=7; шаг Δx=0.5
Значения
Требуется найти интерполяционный полином, график которого проходит через узловые точки интерполяции.
Чтобы найти этот полином,
надо определить его коэффициенты ai. Для определения коэффициентов, составляется система уравнений. Если количество узлов интерполяции 11 (в нашем случае), то полином 10 степени. Количество коэффициентов аi также равно11.
Слайд 9Интерполяция полиномом: расчет коэффициентов матричным методом
Система уравнений для нахождения переменных ai
где A- вектор-столбец переменных ai ( коэффициентов полинома): А=(a1 ; a2 ; a3 ; a4; a5 ; a6 ; a7; a8 ; a9 ; a10 ; a11).
W=матрица Вандермонда
Wij=xin-j степени аргументов в узлах интерполяции
Y- вектор-столбец значений f(x) в узлах интерполяции
Y=(y1 ;y2 ;y3 ;y4 ;y5 ;y6; y7 ;y8 ;y9 ;y10 ;y11)
Матричное решение системы линейных алгебраических уравнений: A=inv(W)*Y
W=
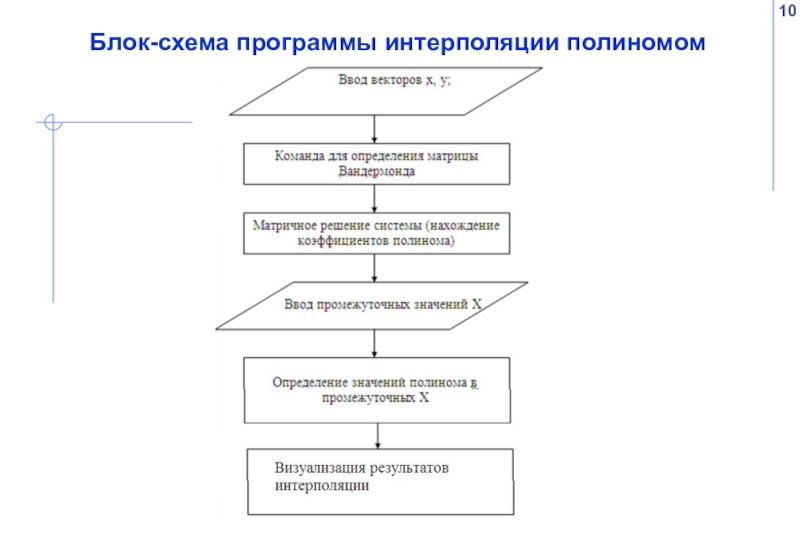
Слайд 11Расчет коэффициентов полинома матричным методом в MATLAB
Решаем данную систему в MATLAB:
>>
>> y=sin(2*x).*sin(x); % определяем значения y в узловых
>> % точках
>> W=vander(x); % определяем матрицу Вандермонда
>> y1=y'; % преобразуем вектор-строку y в вектор->>%столбец
>> A=inv(W)*y1; % решаем систему уравнений, находим >>% значения коэффициентов интерполяционного полинома
Слайд 12Значения коэффициентов полинома
A =
0.00
1.39
-14.24
91.86
-386.76
1067.07
-1882.63
1993.82
-1100.64
215.23
a1=0; a2=-0.08; a3=1.39; a4=-14.24; a5=91.86; a6=-386.76;
a7=1067.07; a8=-1882.63; a9=1993.82; a10=-1100.64; a11=215.23
Интерполяционный полином:
Р=0*а^10-0.08*а^9+1.39а8-
-14.24а7+91.86а6-
-386.76*а^5+1067.07*а^4-
-1882.63*а^3+199.82*а^2-
-1100.64*а+215.23
Слайд 13Расчет промежуточных значений функции в MATLAB при помощи полинома
>> p=a; %
>> x1=2:0.25:7; % задаем промежуточные значения х
>> y1=polyval(p,x1); % вычисляем значения полинома в >>%промежуточных х
>> plot(x,y,x1,y1); %распечатываем графики табличной
>> %функции и интерполирующей функции
Слайд 15Глобальная или локальная?
Пример:
>> x=2:0.25:15; % задаем узловые точки
>> length(x)% определяем размерность
ans =
53 % массив х состоит из 53-х элементов
>> y=sin(2*x).*sin(x); % задаем значения функции в узловых точках
>> W=vander(x); % определяем матрицу Вандермонда
>> y1=y‘ % преобразуем вектор-строку y в вектор столбец
>> a=inv(W)*y1; % вычисляем коэффициенты
Warning: Matrix is close to singular or badly scaled.% предупреждение
Results may be inaccurate. RCOND = 2.790744e-074.
Система плохо обусловлена. Возможна ошибка.
Вывод: При большом количестве узлов интерполяции трудно вычислить интерполяционный полином. MATLAB выдает сообщение о некорректной постановке задачи.
В этом случае применяется локальная интерполяция.
Слайд 16
Линейная интерполяция
Узловые точки соединяются отрезками прямых
xi
xi+1
Интерполяция сплайнами
(spline (англ.) –
Интерполяция квадратичными сплайнами - через узловые точки проводят отрезки квадратичной параболы.
Интерполяция кубическими сплайнами - через узловые точки проводят отрезки кубической параболы.
xi
xi+1
xi-1
Локальная (кусочно-полиномиальная) интерполяция
На каждом интервале [xi , xi+1 ] строится отдельный интерполяционный полином невысокой степени
Слайд 17Локальная интерполяция функции в MATLAB
Для одномерной табличной интерполяции используется функция interp1:
yi = interp1(x, y, xi, method) — позволяет с помощью параметра method задать метод интерполяции:
'nearest' — ступенчатая интерполяция (по соседним элементам);
'linear' — линейная интерполяция (принята по умолчанию);
'spline' — кубическая сплайн-интерполяция;
'cubic' или 'pchip' — интерполяция многочленами Эрмита.
Выходным аргументом interp1 является вектор промежуточных значений аргументов.
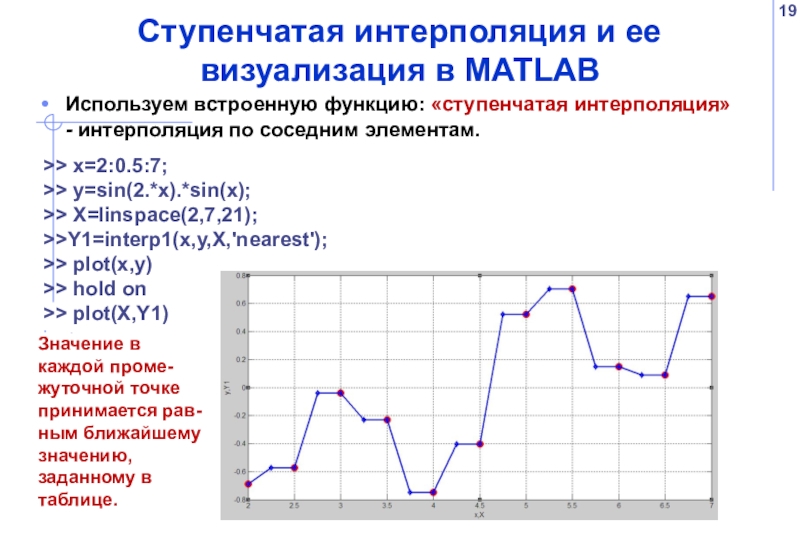
Слайд 19Ступенчатая интерполяция и ее визуализация в MATLAB
Используем встроенную функцию: «ступенчатая интерполяция»
>> x=2:0.5:7;
>> y=sin(2.*x).*sin(x);
>> X=linspace(2,7,21);
>>Y1=interp1(x,y,X,'nearest');
>> plot(x,y)
>> hold on
>> plot(X,Y1)
.
Значение в каждой проме-жуточной точке принимается рав-ным ближайшему значению, заданному в таблице.
Слайд 20Линейная интерполяция и ее визуализация в MATLAB
>> Y=interp1(x,y,X,'linear');
>> plot(x,y)
>> hold on
>>
Используем встроенную функцию: «линейная интерполяция».
Соединение соседних точек отрезками прямых - табличные данные приближаются ломаной линией .
Слайд 21Интерполяция кубическими сплайнами и ее визуализация в MATLAB
>> Y2=interp1(x,y,X,'spline');
>> plot(x,y)
>> hold
>> plot(X,Y2)
Интерполяция кубическими сплайнами – кривыми 3ей степени - обеспечивает отсутствие сильных перегибов кривых в узлах интерполяции. Непрерывность функции и ее 1 и 2 производных на всем интервале интерполирования.
Используем встроенную функцию: «интерполяция кубическими сплайнами».
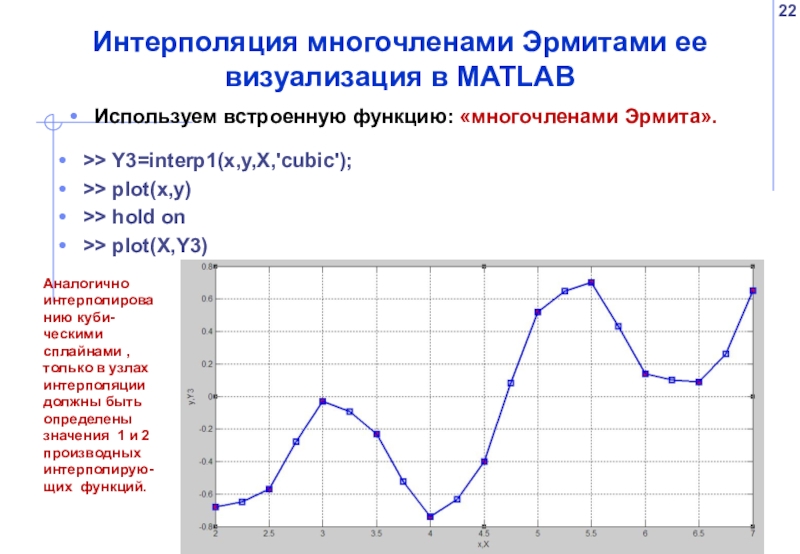
Слайд 22Интерполяция многочленами Эрмитами ее визуализация в MATLAB
>> Y3=interp1(x,y,X,'cubic');
>> plot(x,y)
>> hold on
>>
Используем встроенную функцию: «многочленами Эрмита».
Аналогично интерполированию куби-ческими сплайнами , только в узлах интерполяции должны быть определены значения 1 и 2 производных интерполирую-щих функций.
Слайд 23Сравнение погрешностей методов интерполяции функции yi=sin(2*X).*sin(X) в MATLAB
Файл-функция для определения погрешности:
function
yi=sin(2.*X).*sin(X);
P=abs(yi-Y);
p=P;
max (p)
end
Слайд 24Погрешность ступенчатой интерполяции:
>> X=linspace(2,7,51);
>> Y=interp1(x,y,X,'nearest');
>> p=pogr(X,Y)
ans =
0.3752
Слайд 25Погрешность линейной интерполяции:
>> X=linspace(2,7,51);
>> Y1=interp1(x,y,X,'linear');
>> p1=pogr(X,Y1)
ans =
0.1400
Слайд 26Погрешность интерполяции кубическими сплайнами:
>> X=linspace(2,7,51);
>> Y2=interp1(x,y,X,'spline');
>> p2=pogr(X,Y2)
ans =
0.0545
Слайд 27Погрешность интерполяции многочленами Эрмита:
>> X=linspace(2,7,51);
>> Y3=interp1(x,y,X,'cubic');
>> p3=pogr(X,Y3)
ans =
0.1046
Вывод: наименьшую
Слайд 28Аппроксимация функций
Аппроксимацией (приближением) функции f(x) называется нахождение такой функции g(x) (аппроксимирующей
Особенность метода - аппроксимирующая функция может быть произвольной.
Наиболее часто встречаются аппроксимация прямой линией (линейная регрессия), аппроксимация полиномом (полиномиальная регрессия), аппроксимация линейной комбинацией произвольных функций.
Слайд 29Аппроксимация функций в MATLAB
Одна из наиболее известных аппроксимаций — полиномиальная. В
– polyfit(x, y, n) – возвращает вектор коэффициентов полинома р(х) степени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х).
Слайд 30Аппроксимация функции y=sin(2x)·sin(x) полиномами
>> x=2:0.5:7;
>> y=sin(2.*x).*sin(x);
>> p=polyfit(x,y,3) % аппроксимация полиномом 3-ей
p =
-0.0113 0.1514 -0.3862 -0.3429
>> x1=2:0.1:7;
>> y1=polyval(p,x1);
>> plot(x,y,x1,y1)
Слайд 32Аппроксимация полиномом 5-й степени
>> p1=polyfit(x,y,5) % аппроксимация полиномом 5-й степени
p1 =
0.0444
>> y2=polyval(p1,x1);
>> plot(x,y,x1,y2)
Слайд 36Влияние степени полинома на вид приближающей функции
При увеличении степени полинома график
Если степень полинома равна n-1, где n – количество узловых точек, то аппроксимирующая кривая проходит через узловые точки, т.е. аппроксимация превращается в интерполяцию.
Если степень полинома больше n, то задача имеет бесконечное множество решений, и MATLAB выводит сообщение об этом. При этом форма приближающей кривой на границах интервала далека от формы кривой аппроксимируемой функции.
Слайд 38Метод наименьших квадратов
Для оценки «близости» функций выбирают тот или иной критерий
Критерием близости в методе наименьших квадратов является требование минимальности суммы квадратов отклонений значений аппроксимирующей функции от экспериментальных точек:
Слайд 39Нахождение приближающей функции в виде линейной функции методом наименьших квадратов
Пусть функция
Требуется найти аппроксимирующую (приближающую) функцию g(x).
Приближающую функцию будем определять в виде:
g(x)=a·x+b
Для нахождения данной функции, необходимо определить параметры a и b.
Слайд 40Нахождение приближающей функции в виде линейной функции методом наименьших квадратов
В результате
Для применения критерия близости в методе наименьших квадратов необходимо найти минимум функции:
Слайд 42Задача
В одной системе координат построить графики табличной функции и аппроксимирующей функции.
Решим
Слайд 43Блок-схема программы нахождения приближающей функции в виде линейной функции методом наименьших
Слайд 44Программа для нахождения приближающей функции в виде линейной функции методом наименьших
M-файл нахождения приближающей линейной функции:
clear all % очищаем рабочую область
x=input(‘вектор значений xi>>');% диалоговый ввод переменных хi
y=input(‘вектор значений yi>>'); % диалоговый ввод переменных yi
n=length(x) % определение размерности вектора х
Mx=sum(x)/n % вычисление коэффициента системы уравнений
My=sum(y)/n % вычисление коэффициента системы уравнений
xy=x.*y; % поэлементное перемножение векторов x и y
Mxy=sum(xy)/n % вычисление коэффициента системы уравнений
x2=x.^2; % поэлементное возведение в квадрат вектора х
Mx2=sum(x2)/n % вычисление коэффициента системы уравнений
A=[Mx2 Mx;Mx 1]; % введение матрицы коэффициентов левой части системы…
уравнений
B=[Mxy;My]; % введение матрицы коэффициентов правой части системы уравнений
ab=inv(A)*B; % решение системы уравнений
a=ab(1) % угловой коэффициент приближающей линейной функции
b=ab(2) % свободный член приближающей линейной функции
Y=a*x+b; % аналитическое выражение для приближающей линейной функции
plot(x,y,x,Y) % построение графиков исходной и приближающей функций
Слайд 45Нахождение приближающей функции в виде линейной функции (задача)
вектор значений хi>>[1 1.5
вектор значений yi>>[67 101 168 202 301 334 404]
n =
7
Mx =
3.400000000000000
My =
2.252857142857143e+002
Mxy =
9.724571428571428e+002
Mx2 =
14.742857142857142
a =
64.874326750448859
b =
4.713003334187988
Слайд 47Путем построения кубического сплайна с помощью стандартной MATLAB процедуры interp1 определить
Задача 1 на закрепление новой темы
Слайд 48Решение задачи 1
>> t=50:50:200;
>> E=[0.299 0.645 1.029 1.44];
>> t1=180;
>> E1=interp1(t,E,t1,'spline')
E1 =
Слайд 49С помощью стандартных MATLAB процедур polyfit и polyval определить сопротивление платинового
Задача 2 на закрепление новой темы
Слайд 50>> t=650:50:950;
>> R=[166.55 174.46 182.23 189.86 197.33 204.66 211.85];
>> p=polyfit(t,R,2)
p
-0.0000 0.1976 50.4029
>> R1=polyval(p,780)
R1 =
186.5429
Решение задачи 2


![Презентация по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций Задача интерполяцииПусть функция f(x) задана таблицей своих значений xi, yi: на Задача интерполяцииПусть функция f(x) задана таблицей своих значений xi, yi: на интервале [a; b]:Задача интерполяции - найти](/img/thumbs/d1c702d8655eaeb619b6f0d22f0e94cf-800x.jpg)
![Презентация по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций Глобальная интерполяцияФункция f(x) интерполируется на всем интервале [a; b] обычно с Глобальная интерполяцияФункция f(x) интерполируется на всем интервале [a; b] обычно с помощью единого интерполяционного полинома.Если количество узловых](/img/thumbs/8f866c5974b33742c0f2dd96e7684cda-800x.jpg)





























![Презентация по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций Нахождение приближающей функции в виде линейной функции (задача)вектор значений хi>>[1 1.5 Нахождение приближающей функции в виде линейной функции (задача)вектор значений хi>>[1 1.5 2.5 3.0 4.5 5.1 6.2]вектор значений](/img/tmb/5/445526/0117806c7dd1322d3f09ed6012f9bf65-800x.jpg)

![Презентация по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций Решение задачи 1>> t=50:50:200;>> E=[0.299 0.645 1.029 1.44];>> t1=180;>> E1=interp1(t,E,t1,'spline')E1 = 1.2731 Решение задачи 1>> t=50:50:200;>> E=[0.299 0.645 1.029 1.44];>> t1=180;>> E1=interp1(t,E,t1,'spline')E1 = 1.2731](/img/thumbs/b5cac11d15a9fcce9a8d8d4eb0906a98-800x.jpg)
![Презентация по дисциплине Компьютерное моделирование Аппроксимация и интерполяция функций >> t=650:50:950;>> R=[166.55 174.46 182.23 189.86 197.33 204.66 211.85]; >> p=polyfit(t,R,2)p >> t=650:50:950;>> R=[166.55 174.46 182.23 189.86 197.33 204.66 211.85]; >> p=polyfit(t,R,2)p = -0.0000 0.1976](/img/thumbs/f6b4d3ab1830a25ecc4167331c5efc48-800x.jpg)





