- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку :Теорема и доказательство.Аксиома.
Содержание
- 1. Презентация к уроку :Теорема и доказательство.Аксиома.
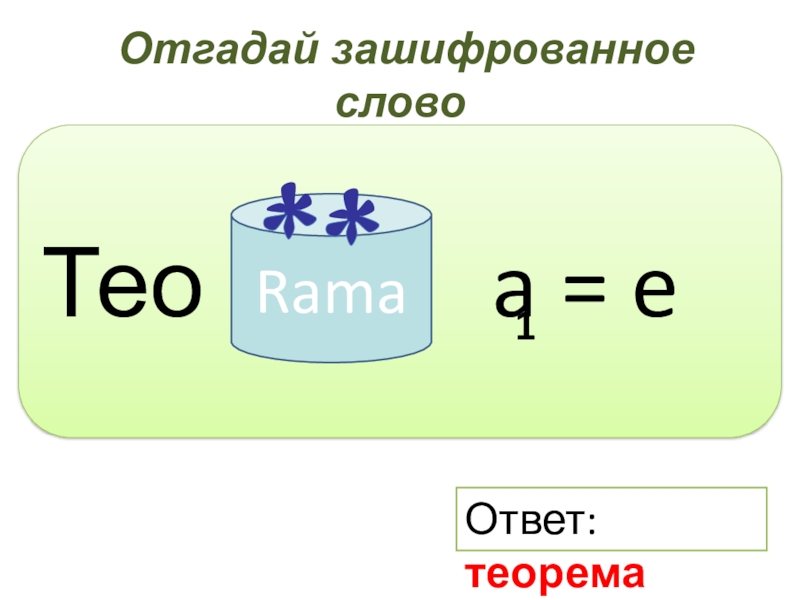
- 2. Отгадай зашифрованное словоТео a = eRama1Ответ: теорема
- 3. Кроссворд
- 4. Слайд 4
- 5. Реши анаграму. КАИСАМО АКСИОМА
- 6. Тема урока: Теорема и доказательство. Аксиома
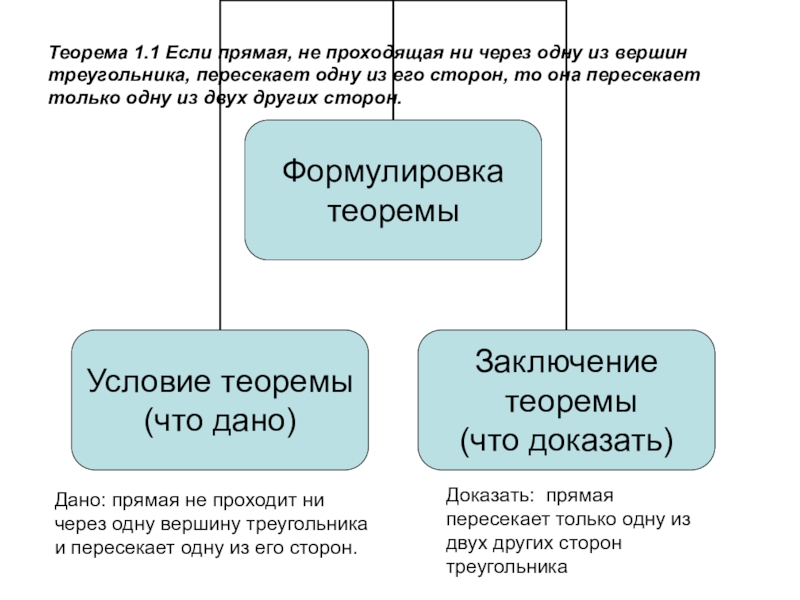
- 7. Теорема 1.1 Если прямая, не проходящая ни
- 8. Теорема 1.1 Если прямая, не проходящая ни
- 9. Теорема 1.1 Если прямая, не проходящая ни
- 10. АксиомаСлово «аксиома» происходит от греческого слова «аксиос» и означает «утверждение, не вызывающее сомнений»
- 11. Вспомним ранее изученные аксиомы, которые мы называли
- 12. III. Каждый отрезок имеет определенную длину, большую
- 13. Самостоятельное решение задач с использованием аксиом планиметрии
- 14. Самопроверка Луч ОВ делит угол АОС
- 15. №2 . Точка С – середина отрезка
- 16. РефлексияНазовите основные понятия урока.Что такое теорема?Что такое аксиома?Что такое доказательство теоремы?В чем смысл доказательства?
- 17. Домашнее заданиеП. 12, 13, все аксиомыТворческое задание: принести рисунки, фотографии на которых запечатлены параллельные прямые.
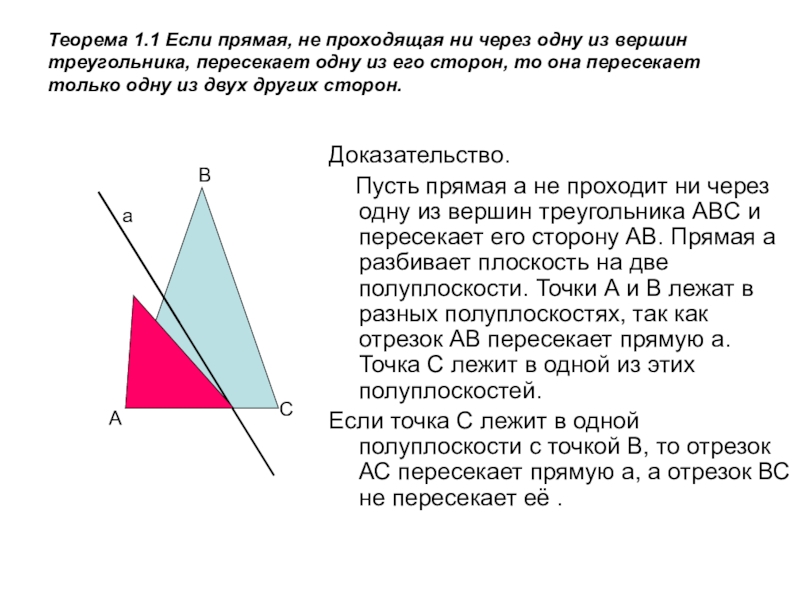
Слайд 7Теорема 1.1 Если прямая, не проходящая ни через одну из вершин
Доказательство.
Пусть прямая а не проходит ни через одну из вершин треугольника ABC и пересекает его сторону АВ. Прямая а разбивает плоскость на две полуплоскости. Точки А и В лежат в разных полуплоскостях, так как отрезок АВ пересекает прямую а. Точка С лежит в одной из этих полуплоскостей.
Если точка С лежит в одной полуплоскости с точкой В, то отрезок АС пересекает прямую а, а отрезок ВС не пересекает её .
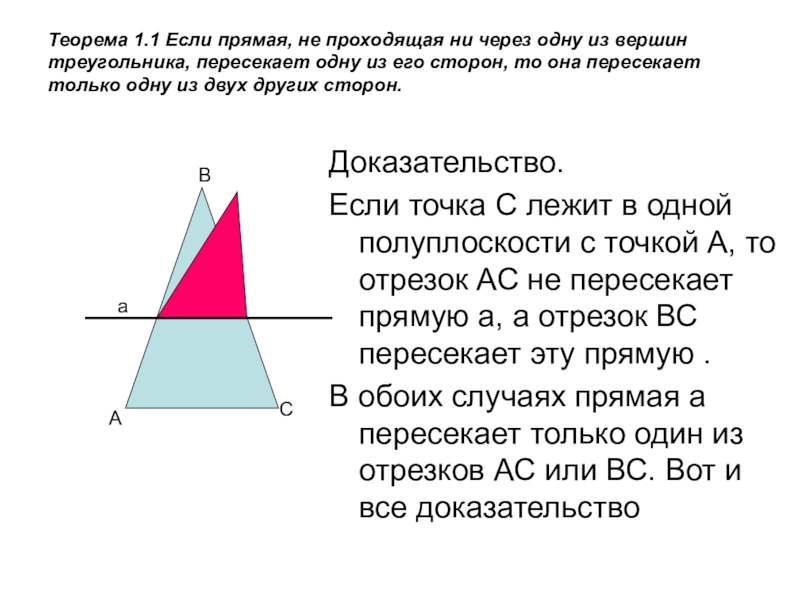
Слайд 8Теорема 1.1 Если прямая, не проходящая ни через одну из вершин
Доказательство.
Если точка С лежит в одной полуплоскости с точкой А, то отрезок АС не пересекает прямую а, а отрезок ВС пересекает эту прямую .
В обоих случаях прямая а пересекает только один из отрезков АС или ВС. Вот и все доказательство
Слайд 9Теорема 1.1 Если прямая, не проходящая ни через одну из вершин
Дано: прямая не проходит ни через одну вершину треугольника и пересекает одну из его сторон.
Доказать: прямая пересекает только одну из двух других сторон треугольника
Слайд 10Аксиома
Слово «аксиома» происходит от греческого слова «аксиос» и означает «утверждение, не
Слайд 11Вспомним ранее изученные аксиомы, которые мы называли основными свойствами:
Какова бы ни
II. Из трех точек на прямой одна и
только одна лежит между двумя
другими.
Слайд 12III. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна
IV. Прямая разбивает плоскость на две полуплоскости.
V.Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
VI. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.
VII. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180, и только один.
VII. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
IX. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Слайд 13Самостоятельное решение задач с использованием аксиом планиметрии
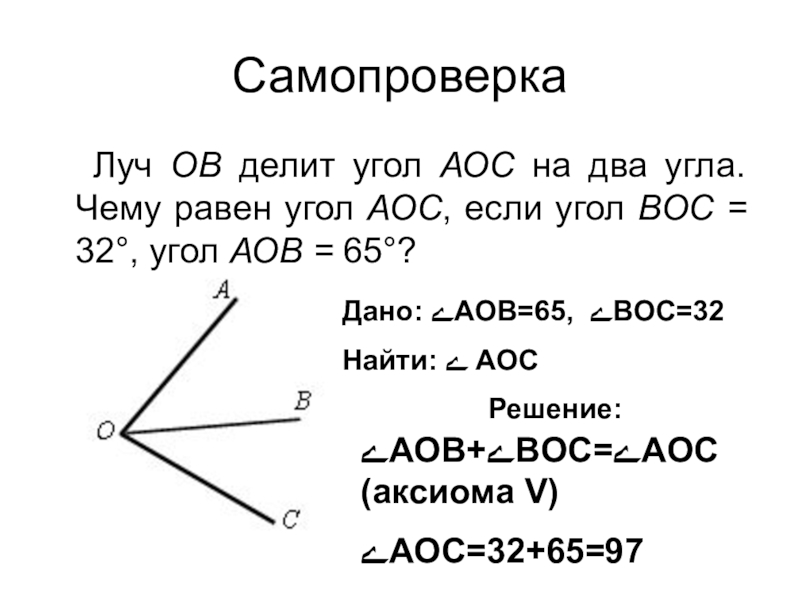
Луч ОВ делит угол АОС
Точка С – середина отрезка АВ, равного 28 см, а точка D – середина отрезка ВС. Чему равна длина отрезка АD?
Слайд 14Самопроверка
Луч ОВ делит угол АОС на два угла. Чему
ےAOB+ےBOC=ےAOC (аксиома V)
ےAOC=32+65=97
Дано: ےAOB=65, ےBOC=32
Найти: ے AOC
Решение:
Слайд 15№2 . Точка С – середина отрезка АВ, равного 28 см,
А
C
В
D
AB=AC+CB (III)
AC=CB, значит 2AC=AB, AC=14 cм.
CD=BD, значит CD=7 cм.
По аксиоме III AD=AC+CD=14+7=21 (cм)
Дано: AB = 28 cм, С-середина AB, D- середина BC
Найти: AD
Решение: