Презентация, доклад к открытому уроку Задание С2: ключевые задачи.

Содержание

Задача 1Найти угол между диагоналями граней куба.

Слайд 1Ключевые задачи
Для заданий с2 из ЕГЭ

Ключевые задачиДля заданий с2 из ЕГЭ

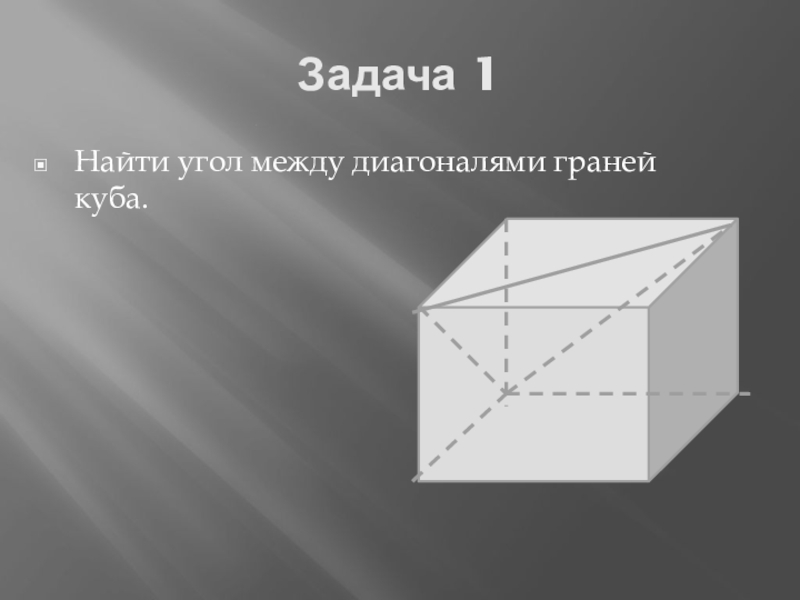
Слайд 2Задача 1
Найти угол между диагоналями граней куба.



Задача 1Найти угол между диагоналями граней куба.

Слайд 3Задача 2
Найти угол между диагональю куба и скрещивающейся с ней диагональю

грани.
Задача 2Найти угол между диагональю куба и скрещивающейся с ней диагональю грани.

Слайд 4задача3
В кубе ABCDA1 B1 C1 D1 диагональ BD1 перпендикулярна плоскостям AB1

C и A1 D C1 и делится ими на три равные части.
задача3В кубе ABCDA1 B1 C1 D1 диагональ BD1 перпендикулярна плоскостям AB1 C и

Слайд 5Задача 4
Найти угол между диагональю куба и плоскостью, проведенной через концы

трех ребер куба, выходящих из той же вершины, что и диагональ.
Задача 4Найти угол между диагональю куба и плоскостью, проведенной через концы трех ребер куба, выходящих из той

Слайд 6задача5
Отрезки, соединяющие середины противолежащих ребер тетраэдра, пересекаются в одной точке и

делятся этой точкой пополам.
задача5Отрезки, соединяющие середины противолежащих ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам.

Слайд 7Расстояние между двумя точками
Расстояние между двумя точками А и В можно

вычислить как длину отрезка АВ, если отрезок АВ удается включить в некоторый треугольник в качестве одной из его сторон.
Расстояние между двумя точкамиРасстояние между двумя точками А и В можно вычислить как длину отрезка АВ, если

Слайд 8Пример 1
В единичном кубе ABCDA1B1C1D1 на диагоналях граней AD1 и

D1B1 взяты точки E и F так, что D1E=1/3 AD1 , D1F=2/3 D1B1. Найдите длину отрезка EF.
Пример 1В единичном кубе ABCDA1B1C1D1 на диагоналях граней AD1 и D1B1 взяты точки E

Слайд 9Дома: решить пример 2.
Пример 2.
Ребра прямоугольного параллелепипеда, основанием которого является квадрат,

равны 1, 4, 4. Найдите расстояние от вершины до центра основания параллелепипеда, не содержащего эту вершину.
Ответ: 3.
Дома: решить пример 2.Пример 2.Ребра прямоугольного параллелепипеда, основанием которого является квадрат, равны 1, 4, 4. Найдите расстояние

Слайд 10Ответы:
1) 125 куб. см;
2) 25 кв. см;
3) 150 кв. см;
4) 5

3;
5) 5 см.
Ответы:1) 125 куб. см;2) 25 кв. см;3) 150 кв. см;4) 5 3;5) 5 см.
Скачать презентацию

Похожие презентации

Дидактическая игра Синквейн Использование дидактических игр как средства развития познавательного интереса на уроках живого мира для детей с ОВЗ в 8 А классе Дидактическая игра Синквейн Использование дидактических игр как средства развития познавательного интереса на уроках живого мира для детей с ОВЗ в 8 А классе 282
Презентация Тема: Фигыль юнәлешләре Презентация Тема: Фигыль юнәлешләре 296
Презентация по теме Теле жап( марийский( государственный) язык Презентация по теме Теле жап( марийский( государственный) язык 202
Презентация к практическому занятию по анатомии и физиологии Кровь. Презентация к практическому занятию по анатомии и физиологии Кровь. 345
Презентация проекта Рисование песком Презентация проекта Рисование песком 464
Обучение в школе или хоумскулинг Обучение в школе или хоумскулинг 193

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть