- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к элективному курсу Развитее пространственных представлений (9 класс)
Содержание
- 1. Презентация к элективному курсу Развитее пространственных представлений (9 класс)
- 2. Геометрия в жизни (многогранники).
- 3. Александрийский маяк В 285 году до н.э.на острове
- 4. Висячие сады Семирамиды Дворец Навуходоносора был построен для
- 5. Галикарнасский мавзолей Лучшие архитекторы того времени построили мавзолей
- 6. Египетские пирамидыОни словно вырастают из песков пустыни
- 7. Храм Артемиды Эфесской Храм достигал 109 метров
- 8. Башня Сююмбике Башня Сююмбике состоит из семи
- 9. Мечеть Кул-Шариф Архитектура этой мечети представляет собой сочетание различных многогранников.
- 10. Никольский собор Нижние ярусы представляют собой параллелепипеды, а верхний ярус – многогранник.
- 11. Платоновы телаПравильные выпуклые многогранники
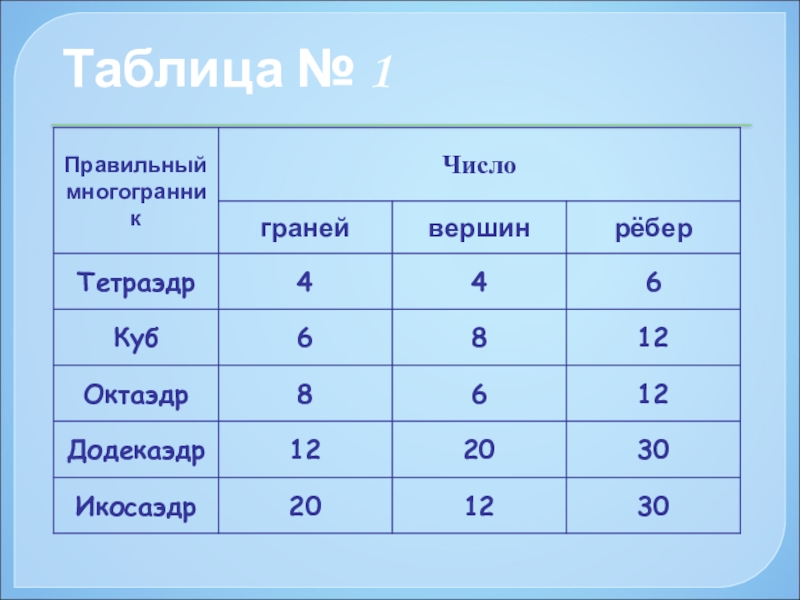
- 12. Правильный тетраэдр Составлен из четырёх равносторонних
- 13. Составлен из восьми равносторонних треугольников. Каждая вершина
- 14. Правильный икосаэдрСоставлен из двадцати равносторонних треугольников. Каждая
- 15. Составлен из шести квадратов. Каждая
- 16. Правильный додекаэдр Составлен из двенадцати правильных пятиугольников.
- 17. Названия многогранников пришли из Древней Греции, в
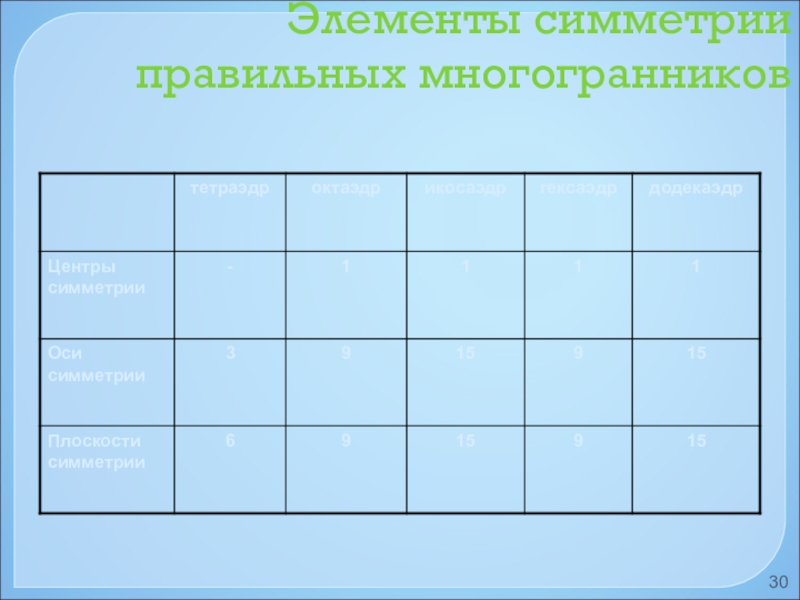
- 18. Таблица № 1
- 19. Сальвадор Дали«Тайная вечеря»
- 20. Правильные многогранники и природа
- 21. Определите количество граней, вершин и рёбер многогранника,
- 22. Правильные многогранники и их построение.
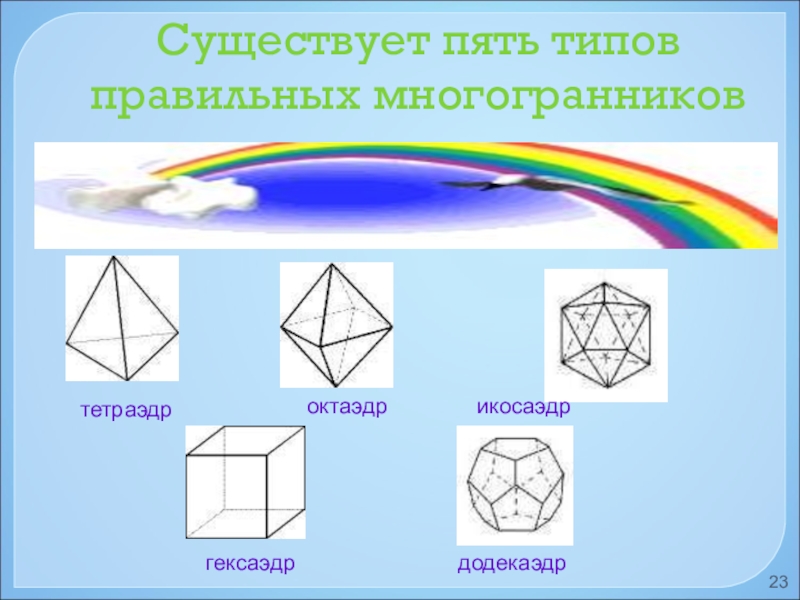
- 23. Существует пять типов правильных многогранниковтетраэдроктаэдрикосаэдргексаэдрдодекаэдр
- 24. Правильным называется многогранник, у которого все грани
- 25. Правильный многогранник, у которого грани правильные треугольники
- 26. ОКТАЭДРПравильный многогранник, у которого грани- правильные
- 27. ИКОСОЭДРПравильный многогранник, у которого грани - правильные
- 28. КУБ -правильный многогранник, у которого грани –
- 29. ДодекаэдрПравильный многогранник, у которого грани правильные пятиугольники
- 30. Элементы симметрии правильных многогранников
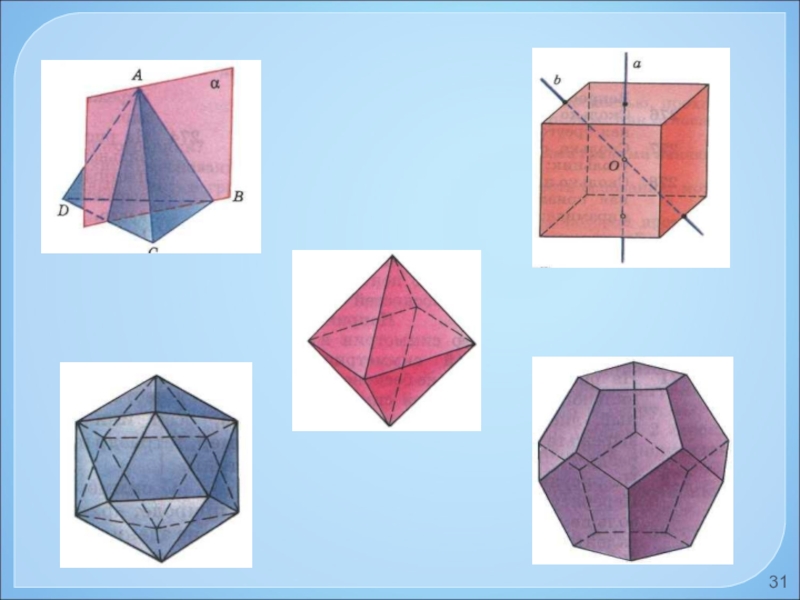
- 31. Слайд 31
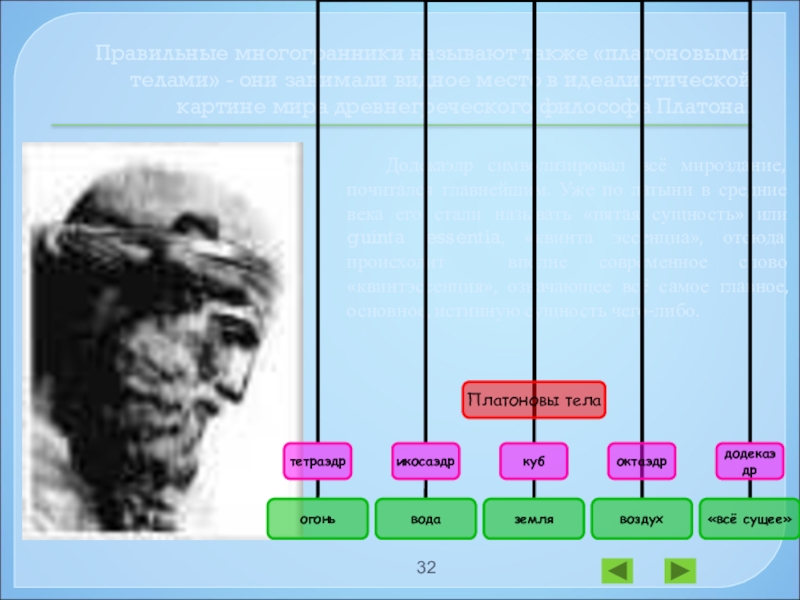
- 32. Правильные многогранники называют также «платоновыми телами» -
- 33. Олицетворение многогранников.
- 34. Дюрер. Меланхолия
- 35. Построение сечений многогранников
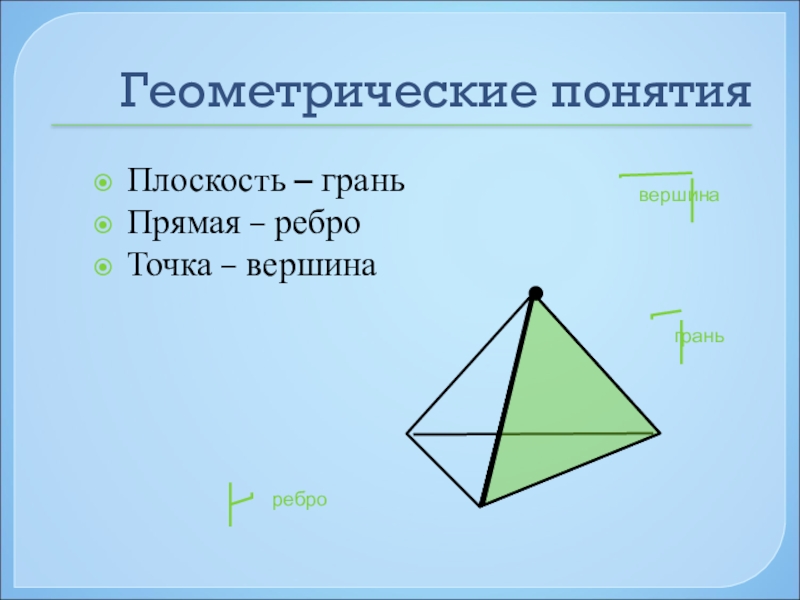
- 36. Геометрические понятияПлоскость – граньПрямая – реброТочка – вершинаграньребровершина
- 37. МногогранникиТетраэдрПараллелепипед
- 38. Геометрические утвержденияЕсли две точки одной прямой лежат в плоскости, то ився прямая лежит в этой плоскости.
- 39. Геометрические утвержденияЕсли две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
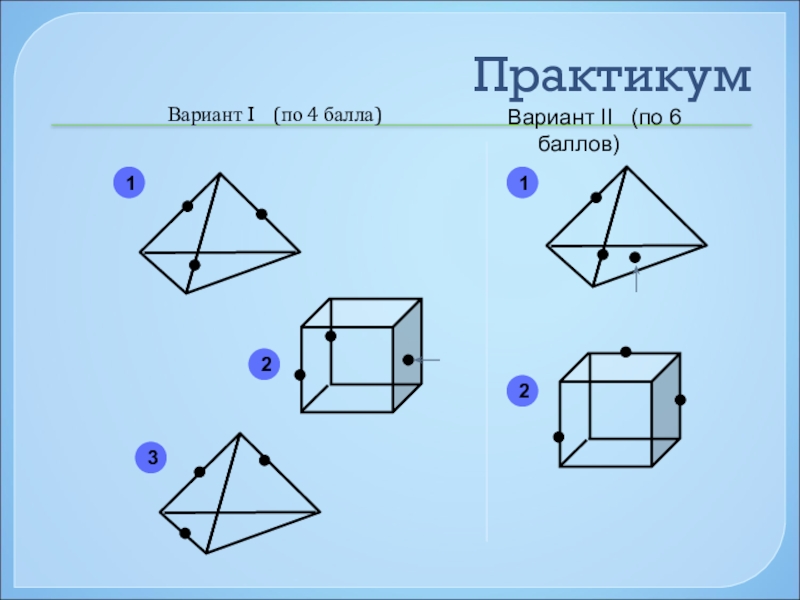
- 40. ПрактикумВариант I (по 4 балла)Вариант II (по 6 баллов)12312
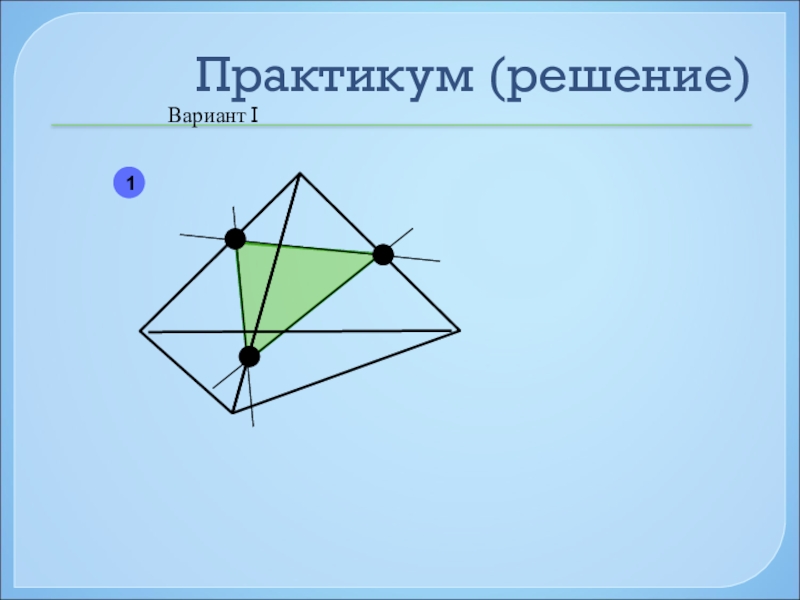
- 41. Практикум (решение)Вариант I1
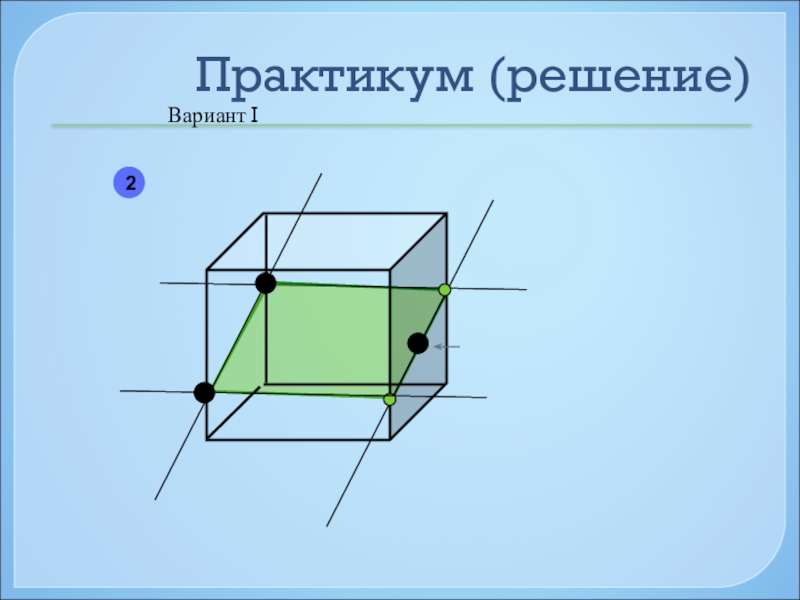
- 42. Практикум (решение)Вариант I2
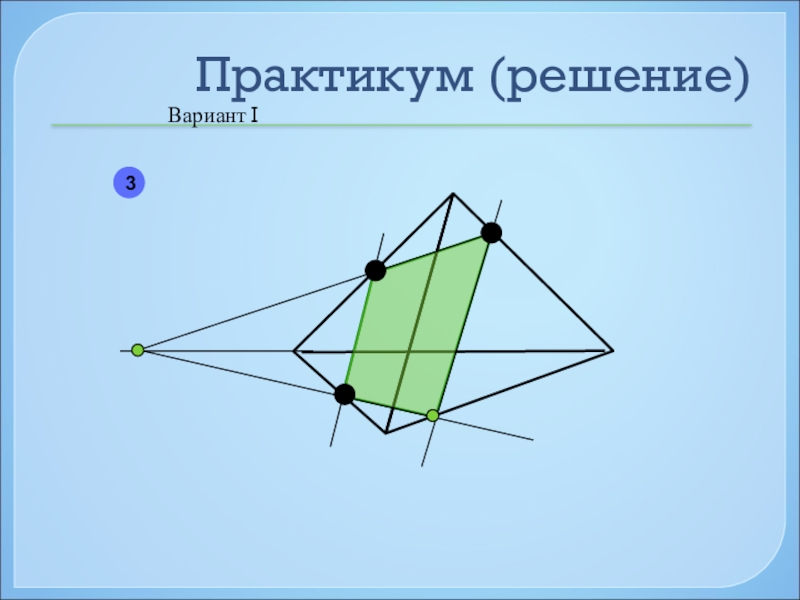
- 43. Практикум (решение)Вариант I3
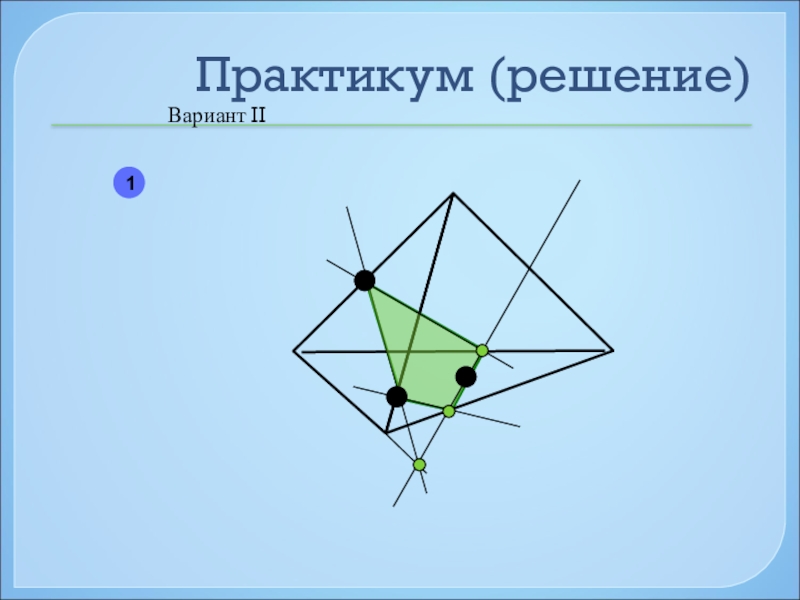
- 44. Практикум (решение)Вариант II1
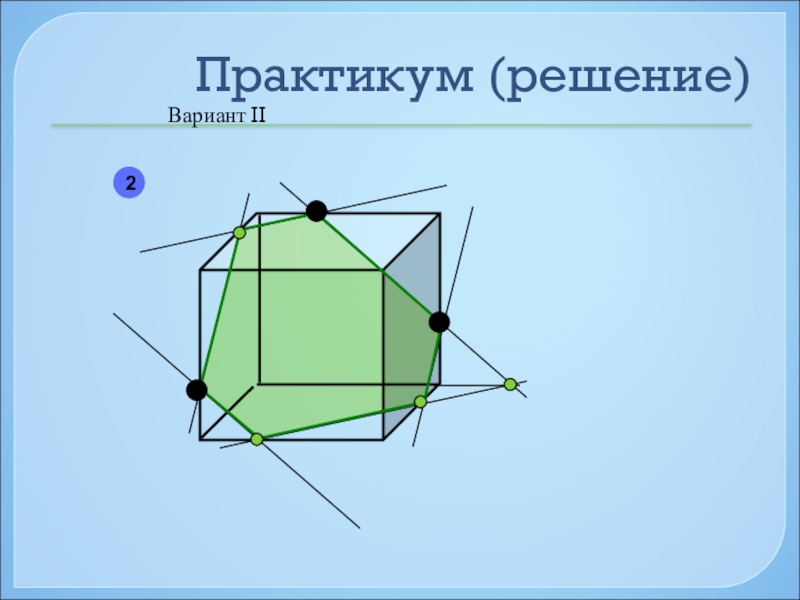
- 45. Практикум (решение)Вариант II2
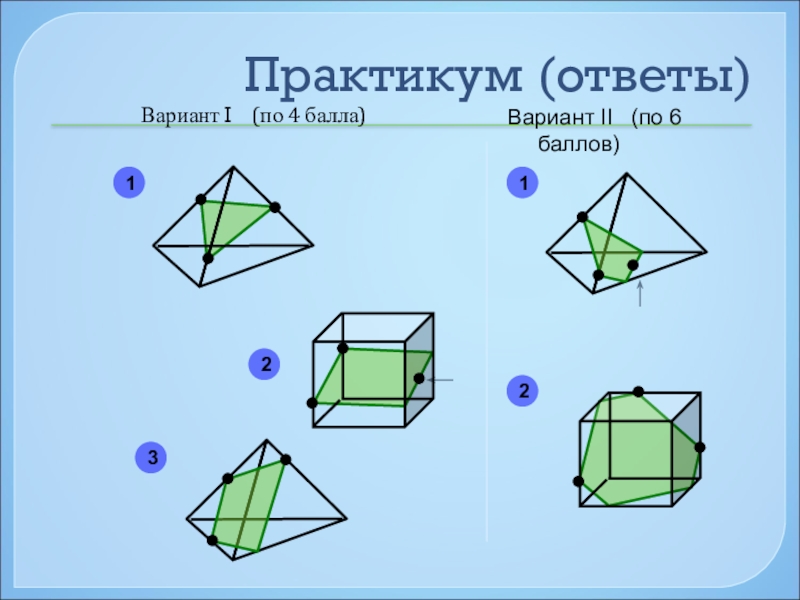
- 46. Практикум (ответы)Вариант I (по 4 балла)Вариант II (по 6 баллов)12312
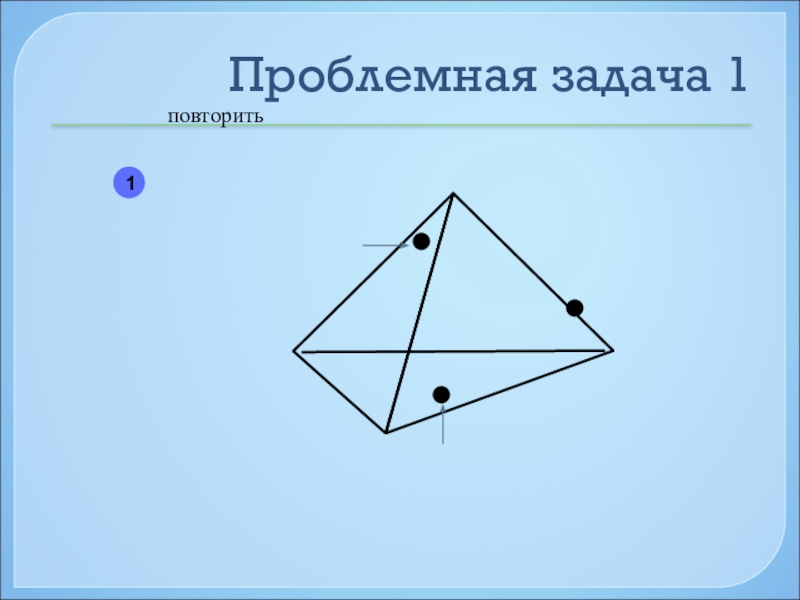
- 47. Проблемная задача 1повторить1
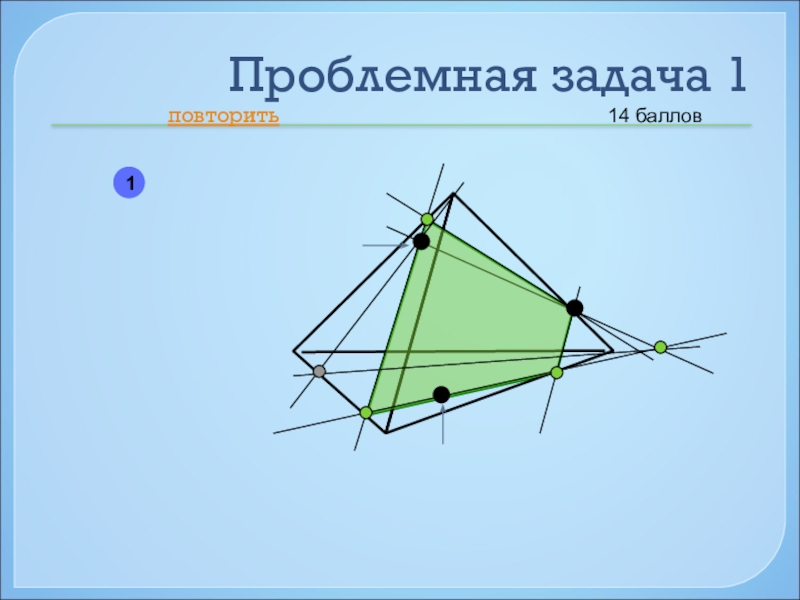
- 48. Проблемная задача 1повторить114 баллов
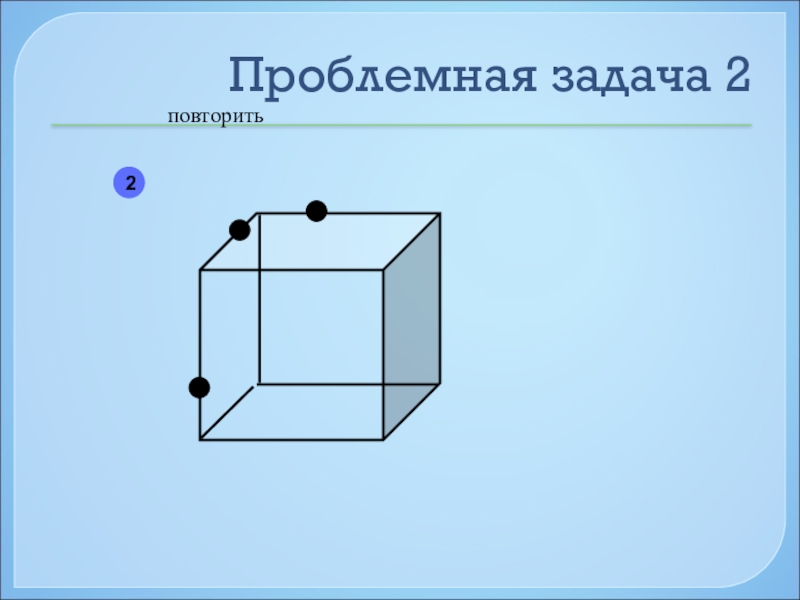
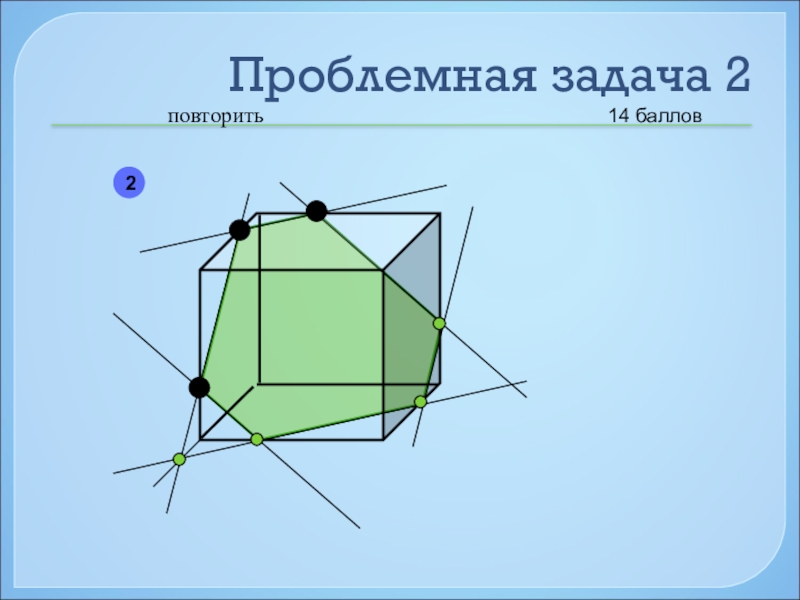
- 49. Проблемная задача 2повторить2
- 50. Проблемная задача 2повторить214 баллов
- 51. Инструкция для построения сеченийПредставьте ситуацию:Ваш одноклассник заболел
- 52. Построение с помощью куба
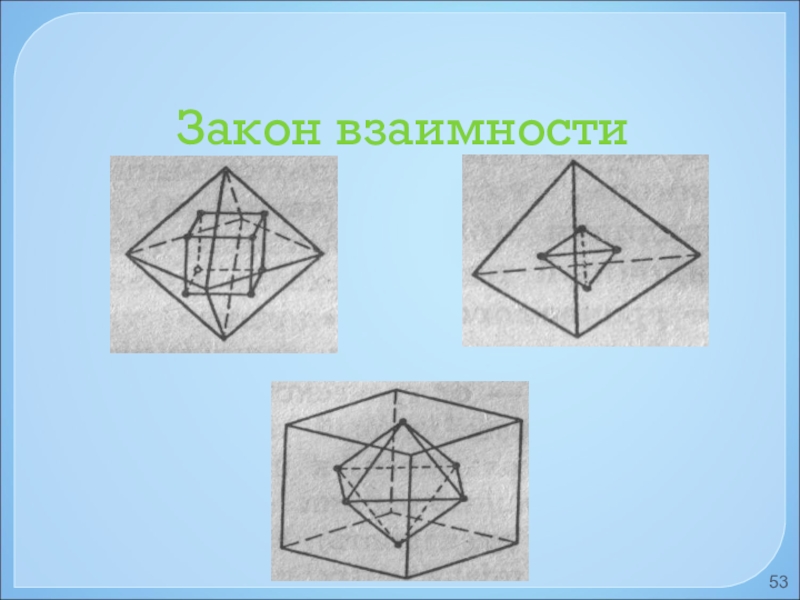
- 53. Закон взаимности
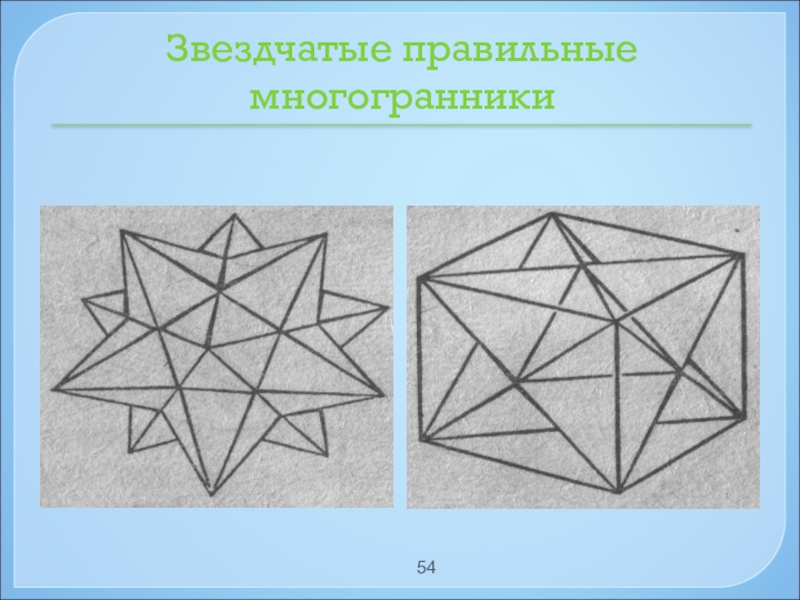
- 54. Звездчатые правильные многогранники
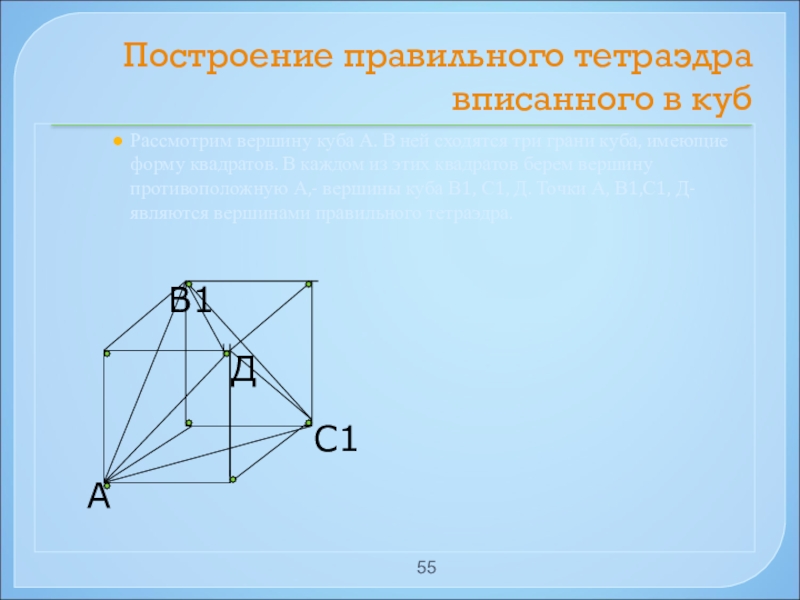
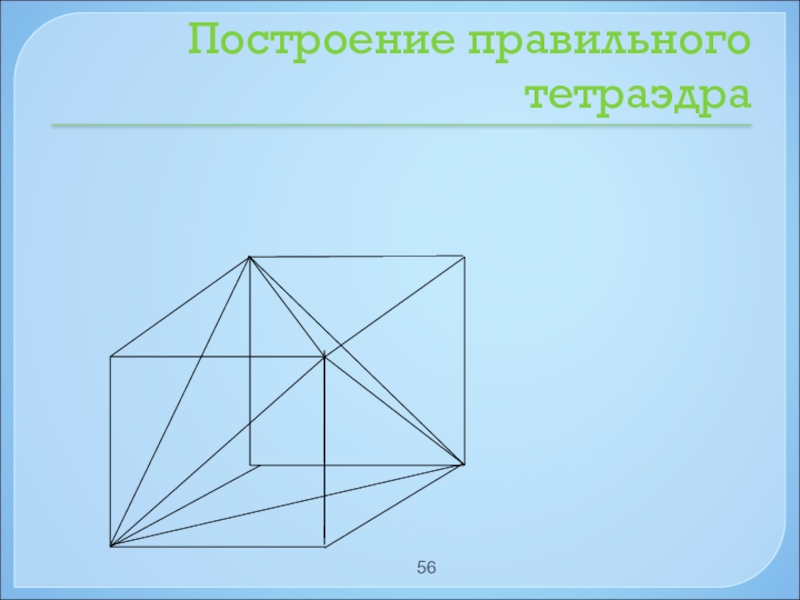
- 55. Построение правильного тетраэдра вписанного в кубРассмотрим вершину
- 56. Построение правильного тетраэдра
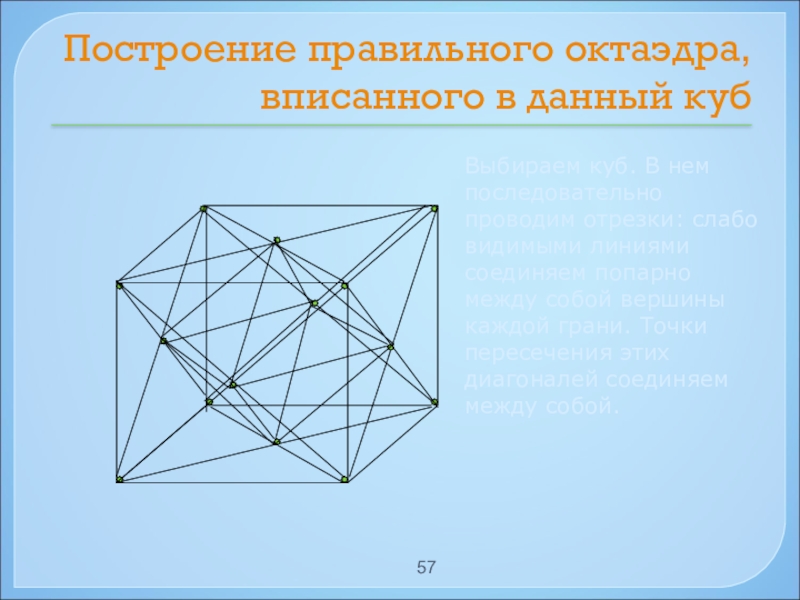
- 57. Построение правильного октаэдра, вписанного в данный кубВыбираем
- 58. Описать около данного куба правильный октаэдрЧерез центры
- 59. Построение икосаэдра, вписанного в кубПоместим на средних
- 60. Построение додекаэдра, описанного около кубаНа каждой грани
- 61. Лобачевский и его геометрия Проблема: Почему возникла "новая" геометрия?
- 62. Гипотеза:Любая теория современной науки считается единственно верной,
- 63. Видите движение на этой картинке?
- 64. Эксперимент «Иллюзии зрения»На рисунке буквы расположены параллельно
- 65. Николай Иванович Лобачевский (1792 – 1856 гг.)Все!
Слайд 1Элективный курс
Развитие пространственных представлений
Учителя математики
высшей категории МОУ «Гимназия
Пшатовой Галины Владимировны
Слайд 3Александрийский маяк
В 285 году до н.э.на острове Фарос архитектор Сострат Книдский
Слайд 4Висячие сады Семирамиды
Дворец Навуходоносора был построен для его жены Семирамиды на
Висячие сады украшали северо- западную часть дворца. На сводчатых арках из кирпича были расположены террасы, напоминающие уступы гор. Поверх кирпичей залит асфальт, на нем – свинцовые плиты, а на них насыпан слой плодородной земли и посажены деревья, кусты и цветы. Издали кажется, что эти сады как бы висят в воздухе.
Слайд 5Галикарнасский мавзолей
Лучшие архитекторы того времени построили мавзолей в виде почти квадратного
Слайд 6Египетские пирамиды
Они словно вырастают из песков пустыни - колоссальные, величествен-ные, подавляющие
Слайд 7Храм
Артемиды Эфесской
Храм достигал 109 метров в длину, 50 - в
Слайд 8Башня Сююмбике
Башня Сююмбике состоит из семи ярусов, нижние ярусы представляют
Слайд 9Мечеть
Кул-Шариф
Архитектура этой мечети представляет собой сочетание различных многогранников.
Слайд 10Никольский собор
Нижние ярусы представляют собой параллелепипеды, а верхний ярус – многогранник.
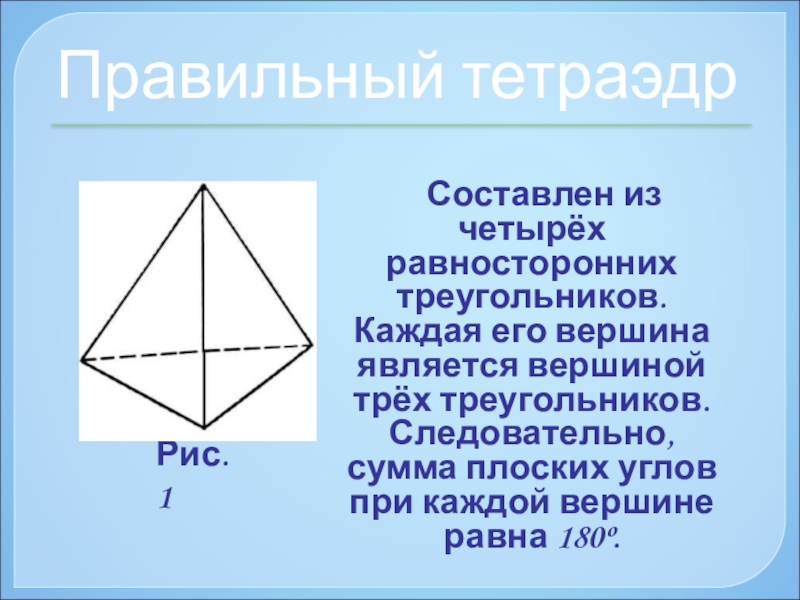
Слайд 12Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина
Рис. 1
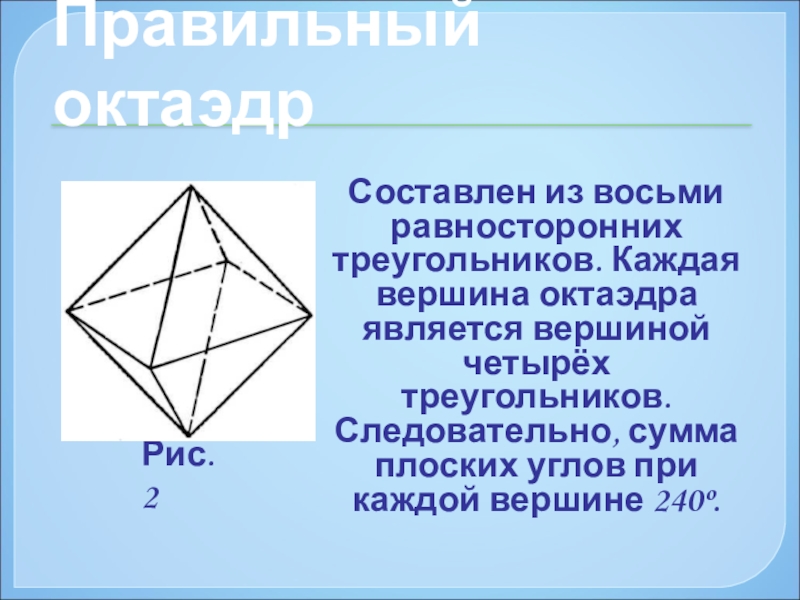
Слайд 13Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх
Правильный октаэдр
Рис. 2
Слайд 14Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной
Рис. 3
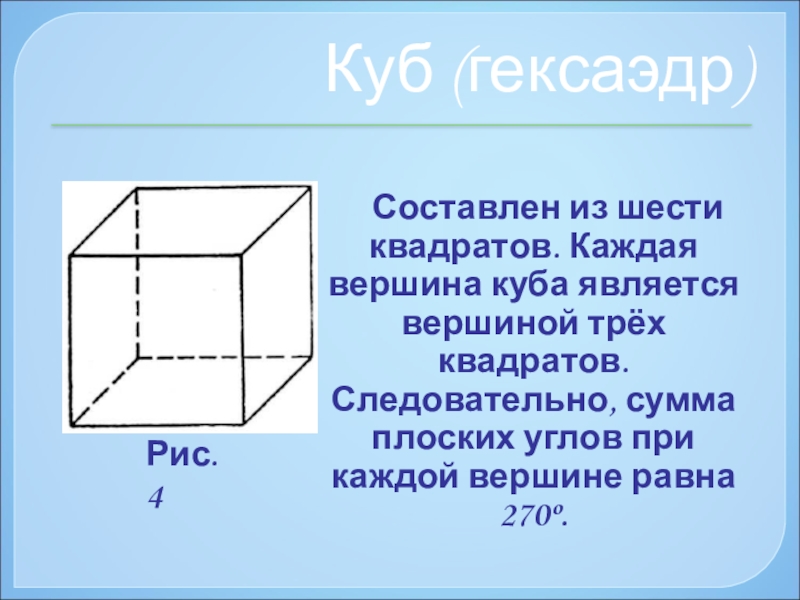
Слайд 15 Составлен из шести квадратов. Каждая вершина куба является вершиной
Куб (гексаэдр)
Рис. 4
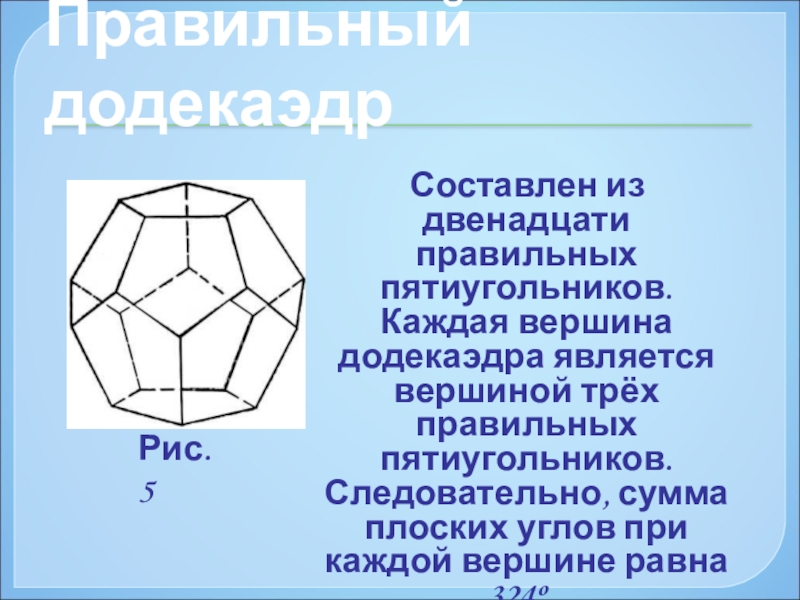
Слайд 16Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является
Рис. 5
Слайд 17Названия многогранников
пришли из Древней Греции,
в них указывается число граней:
«эдра»
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
Слайд 20Правильные многогранники и природа
Правильные многогранники встречаются в
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.
При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых имеет форму правильного октаэдра.
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.
Феодария
(Circjgjnia icosahtdra)
Рис. 8
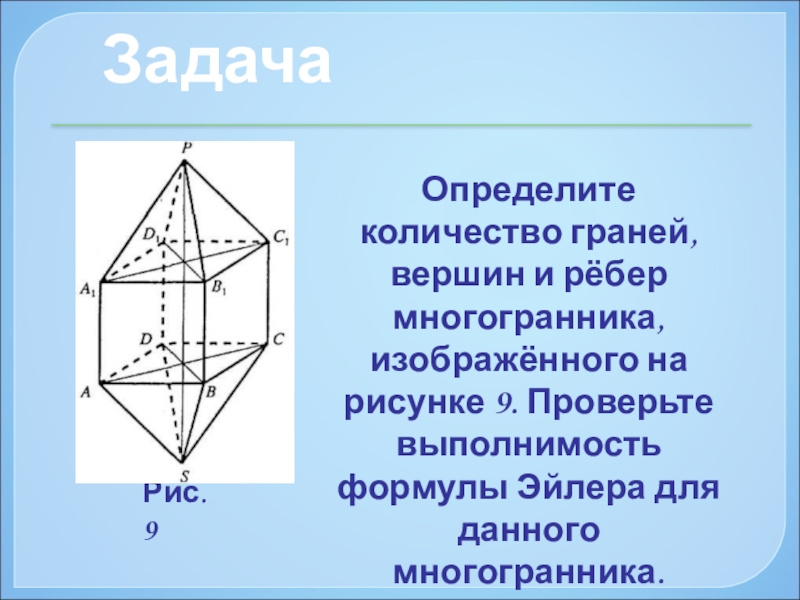
Слайд 21Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке 9.
Задача
Рис. 9
Слайд 24Правильным называется многогранник, у которого все грани являются правильными многоугольниками, и
Приведён пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.
Слайд 25
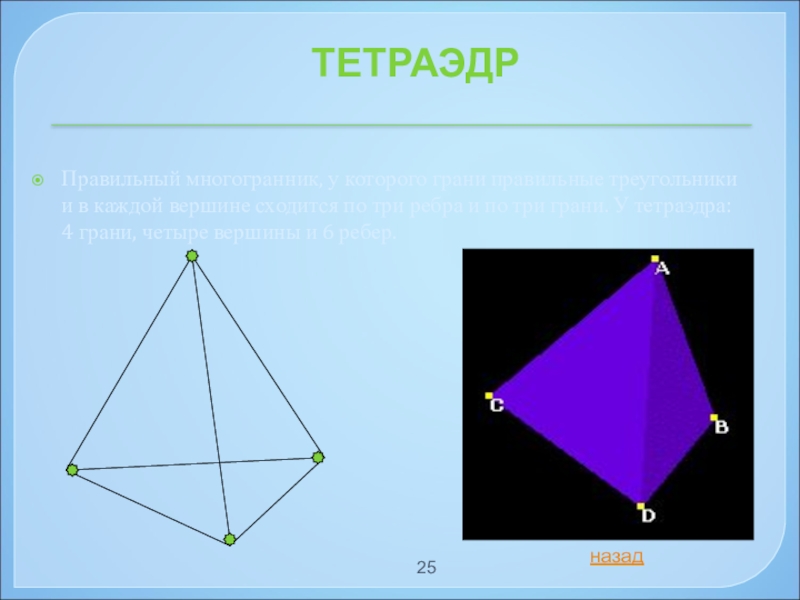
Правильный многогранник, у которого грани правильные треугольники и в каждой вершине
назад
ТЕТРАЭДР
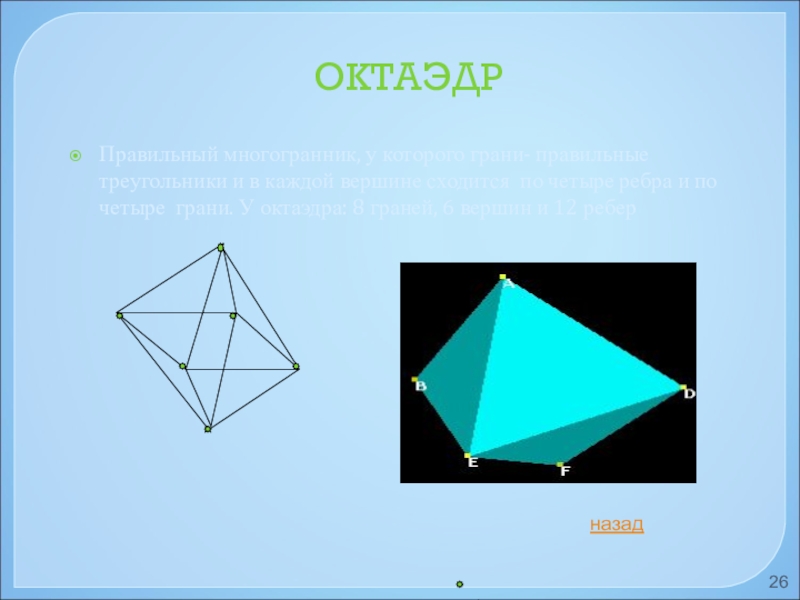
Слайд 26 ОКТАЭДР
Правильный многогранник, у которого грани- правильные треугольники и в каждой
назад
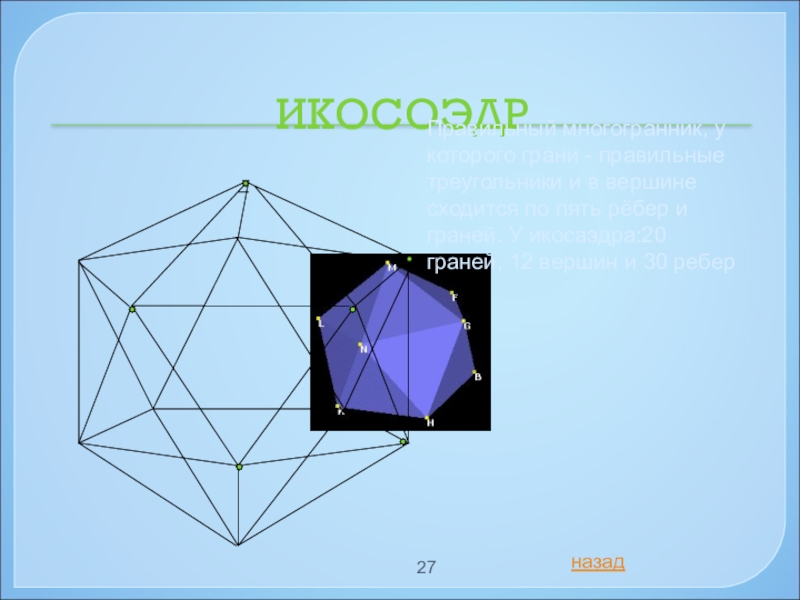
Слайд 27ИКОСОЭДР
Правильный многогранник, у которого грани - правильные треугольники и в вершине
назад
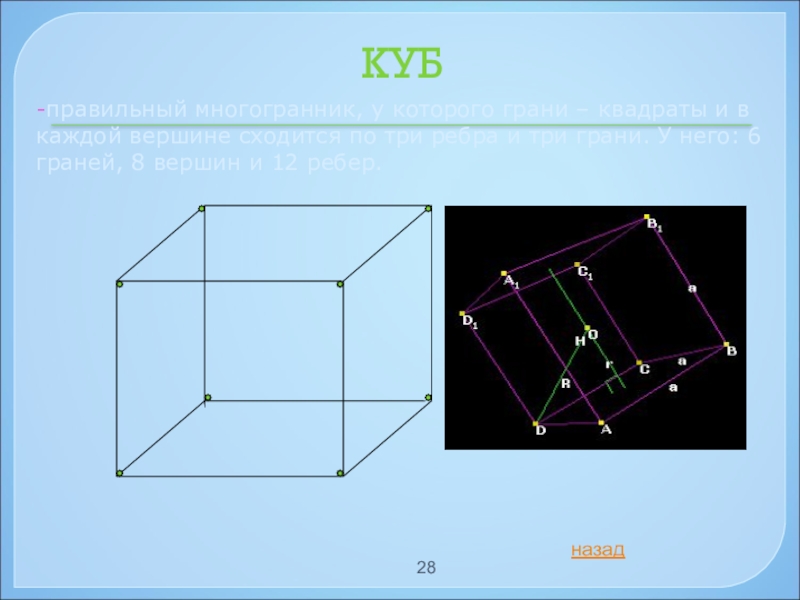
Слайд 28КУБ
-правильный многогранник, у которого грани – квадраты и в каждой
назад
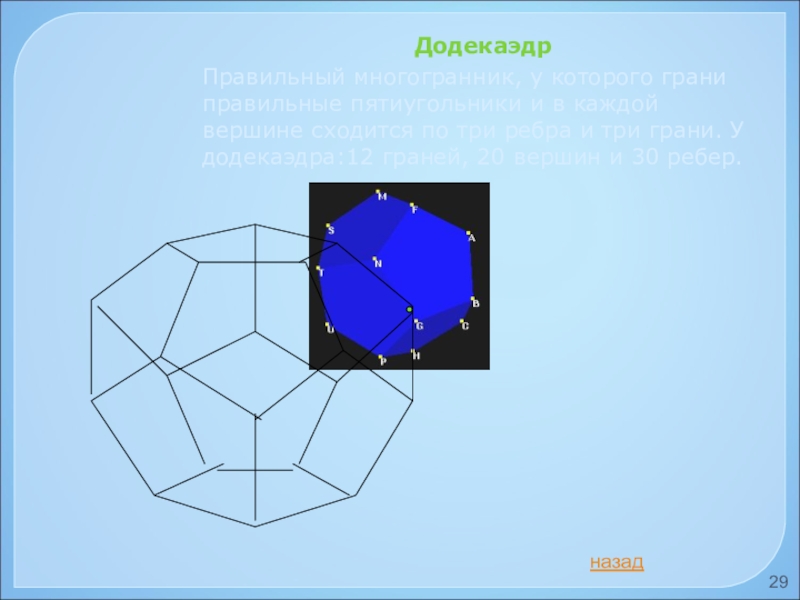
Слайд 29Додекаэдр
Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине
назад
Слайд 32Правильные многогранники называют также «платоновыми телами» - они занимали видное место
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.
Слайд 38
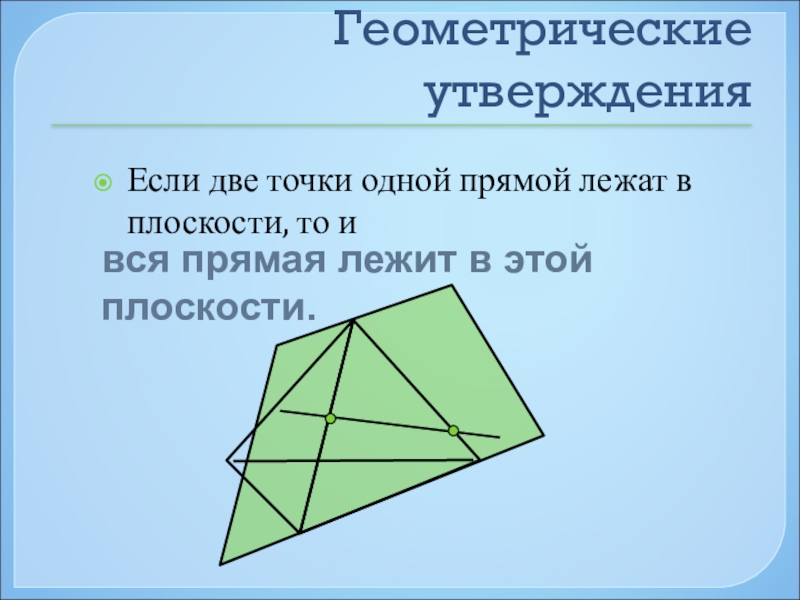
Геометрические утверждения
Если две точки одной прямой лежат в плоскости, то и
вся
Слайд 39Геометрические утверждения
Если две параллельные плоскости пересечены третьей, то
линии их пересечения
Слайд 51Инструкция для построения сечений
Представьте ситуацию:
Ваш одноклассник заболел и пропустил уроки, на
Вам нужно по телефону объяснить эту тему. Сформулируйте и запишите пошаговую инструкцию.
Слайд 55Построение правильного тетраэдра вписанного в куб
Рассмотрим вершину куба А. В ней
С1
В1
А
Д
Слайд 57Построение правильного октаэдра, вписанного в данный куб
Выбираем куб. В нем последовательно
Слайд 58Описать около данного куба правильный октаэдр
Через центры противоположных
граней куба проведем
которые пересекаются в точке О- центре куба- и являются взаимно перпендикулярными. На каждой из этих прямых по обе стороны от точки О отложим отрезки длиной 1,5 а,
Где а- длина ребра куба. Концы этих отрезков являются вершинами правильного октаэдра. Далее последовательно соединяем эти вершины.
O
Слайд 59Построение икосаэдра, вписанного в куб
Поместим на средних линиях граней куба по
Слайд 60Построение додекаэдра, описанного около куба
На каждой грани куба строим « четырехскатную
Слайд 62Гипотеза:
Любая теория современной науки считается единственно верной, пока не создана следующая.
Был мудрым Евклид,
Но его параллели,
Как будто бы вечные сваи легли.
И мысли его, что как стрелы летели,
Всегда оставались в пределах Земли.
А там, во вселенной, другие законы,
Там точками служат иные тела.
И там параллельных лучей миллионы
Природа сквозь Марс, может быть, провела.
Цель:
Найти доказательство того, что истинно утверждение «через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и параллельные ей»
Слайд 64Эксперимент «Иллюзии зрения»
На рисунке буквы расположены параллельно (стоят прямо) или нет?
1
ИТОГИ опроса:
всего параллельно нет
300 3% 97%
Ответ: параллельно.
всего спираль окружности
300 100% 0%
Ответ: окружности.
На рисунке изображена спираль или несколько
окружностей?
2
ВЫВОД: В геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.
Положительный момент: благодаря зрительным искажениям существует живопись.
Если интересно
Слайд 65Николай Иванович Лобачевский
(1792 – 1856 гг.)
Все! Перечеркнуты “Начала”.
Довольно мысль на
Хоть прав почти во всем Евклид,
Но быть не вечно постоянству:
И плоскость свернута в пространство,
И мир
Иной имеет вид...
Краткое описание геометрии Лобачевского.
ВЫВОД: Заменив V постулат евклидовой геометрии на аксиому, Лобачевский пришел к выводу, что можно построить другую геометрию, отличную от евклидовой.