доказательствах, которые, казалось бы, связаны только умом. Но это означало бы, что мы забываем о чувстве математической красоты, чувстве гармонии чисел и формы, геометрической выразительности. Это настоящее эстетическое чувство, знакомое всем математикам.
Б. Мандельброт, американский математик, “отец” теории фракталов
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Фракталы: наука и искусство 21 века
Содержание
- 1. Презентация Фракталы: наука и искусство 21 века
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Фракталы: наука и искусство XXI века
- 9. ЦЕЛЬ РАБОТЫ исследование и изучение основ фрактальной
- 10. ОСНОВНЫЕ НАПРАВЛЕНИЯ РАБОТЫ История появленияОпределение фракталаПримеры фракталовКлассификация фракталовПрименение фракталовЗаключение Фракталы в природе
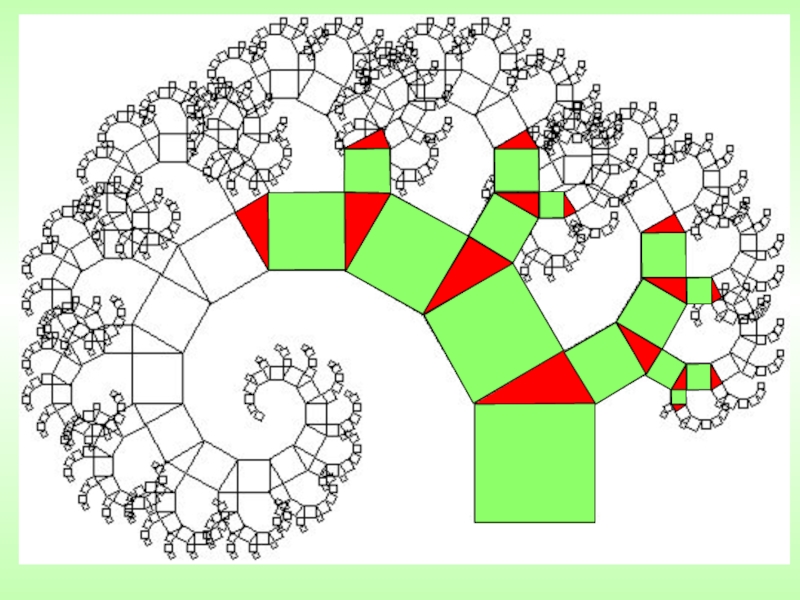
- 11. Фрактал - геометрическая фигура, состоящая из
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. ФРАКТАЛЫ В ПРИРОДЕ
- 16. Примеры фракталов
- 17. Примеры фракталов
- 18. Примеры фракталов
- 19. Примеры фракталов
- 20. Примеры фракталов
- 21. Примеры фракталов
- 22. Примеры фракталов
- 23. Примеры фракталов
- 24. Примеры фракталов
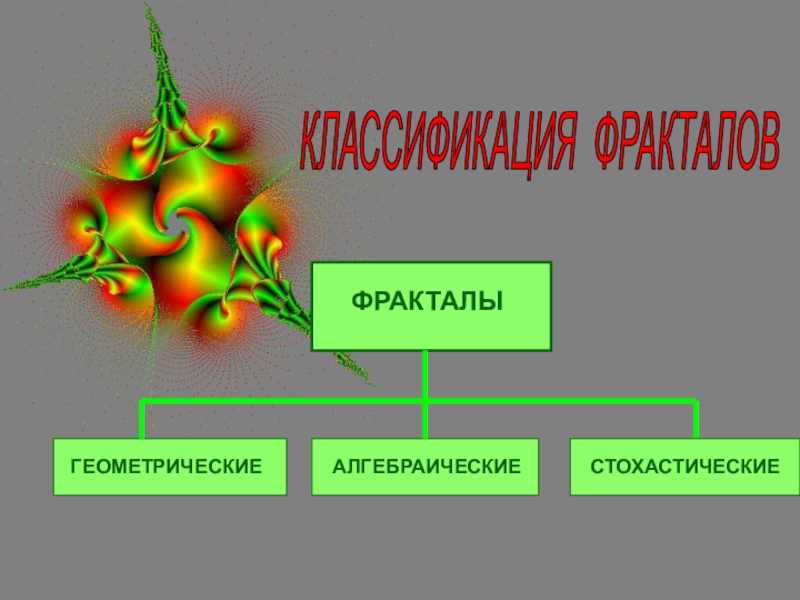
- 25. КЛАССИФИКАЦИЯ ФРАКТАЛОВ ГЕОМЕТРИЧЕСКИЕ
- 26. Это «функции - монстры», которых так
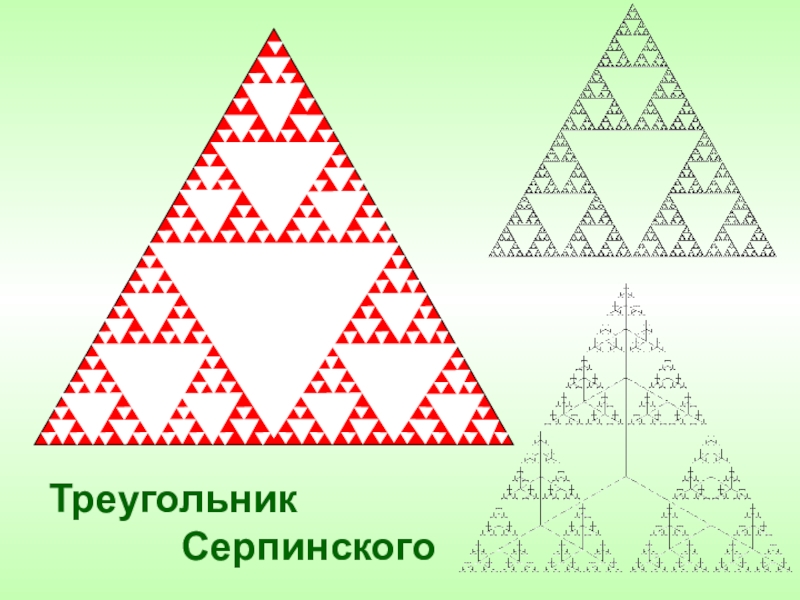
- 27. Треугольник Серпинского
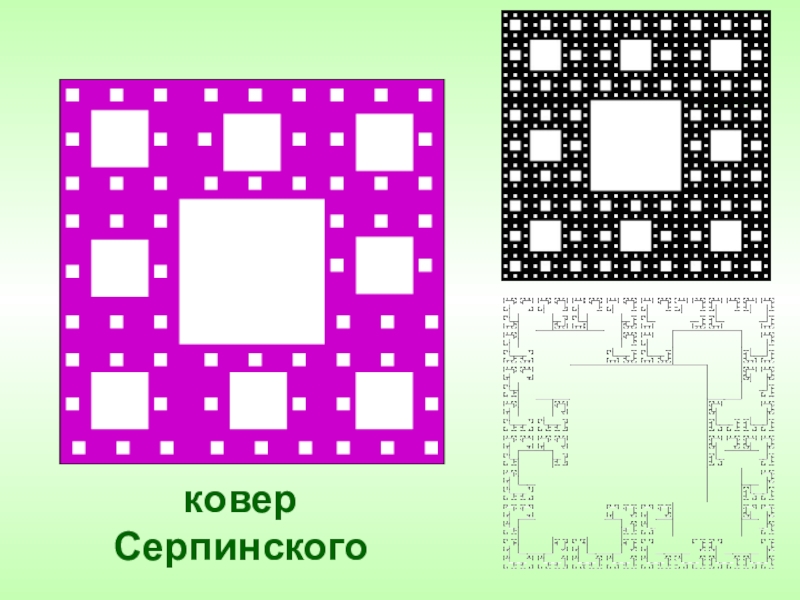
- 28. ковер Серпинского
- 29. Слайд 29
- 30. Слайд 30
- 31. Это фракталы, которые можно построить, используя простые
- 32. Множество ЖюлиаЦвет каждой точки зависит от того,
- 33. Слайд 33
- 34. МНОЖЕСТВО МАНДЕЛЬБРОТА (окрашено лиловым цветом). Картинка получается
- 35. Это фракталы, при
- 36. Слайд 36
- 37. Слайд 37
- 38. 1. Проанализирована и проработана литература по теме
- 39. «Фракталы - это глубокая философская идея, впервые
- 40. Страница авторов: Власова Алина и Симонова
Фракталы: наука и искусство XXI века «Есть в математике нечто, вызывающее человеческий восторг»Ф. Хаусдорф, немецкий математик
Слайд 8Фракталы: наука и искусство XXI века
«Есть в математике нечто, вызывающее человеческий восторг»
Ф. Хаусдорф, немецкий математик
Слайд 9ЦЕЛЬ РАБОТЫ
исследование и изучение основ фрактальной теории, знакомство с математическим
обоснованием графической интерпретации фрактальных образов
МЕТОДЫ ИЗУЧЕНИЯ
Анализ литературы по теме исследования,
Изучение фракталов различного вида,
Разработать классификацию фракталов,
Собрать коллекцию фрактальных образов.
Слайд 10ОСНОВНЫЕ НАПРАВЛЕНИЯ РАБОТЫ
История появления
Определение фрактала
Примеры фракталов
Классификация фракталов
Применение фракталов
Заключение
Фракталы в
природе
Слайд 11
Фрактал - геометрическая фигура, состоящая из частей, которые могут быть
поделены на части, каждая из которых будет представлять уменьшенную копию целого.
Fractal от латинского слова fractus, означает разбитый (поделенный на части).
Основное свойство фракталов: самоподобие, в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.
Fractal от латинского слова fractus, означает разбитый (поделенный на части).
Основное свойство фракталов: самоподобие, в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.
ПОНЯТИЕ ФРАКТАЛА
Слайд 26 Это «функции - монстры», которых так называли за недифференцируемость в
каждой точке.
Геометрические фракталы являются также самыми наглядными, т.к. сразу видна самоподобность.
Для построения геометрических фракталов характерно задание «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.
Геометрические фракталы являются также самыми наглядными, т.к. сразу видна самоподобность.
Для построения геометрических фракталов характерно задание «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.
ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ
Слайд 31Это фракталы, которые можно построить, используя простые алгебраические формулы.
Получают их с
помощью нелинейных процессов в n–мерных пространствах.
Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона
Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона
АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ
Слайд 32Множество Жюлиа
Цвет каждой точки зависит от того, сколько итераций комплексной функции
может
быть сделано, пока точка z не выйдет за пределы круга радиуса r
Здесь z — комплексное число, соответствующее точке .
Множество Жюлиа — это множество таких точек, что отображения вида
не отображают их в окрестность бесконечности. На рисунке эти точки окрашены лиловым цветом.
Картинка получена выбором параметров a = 1.8, и b = 0.2 i и поворотом на 900
Здесь z — комплексное число, соответствующее точке .
Множество Жюлиа — это множество таких точек, что отображения вида
не отображают их в окрестность бесконечности. На рисунке эти точки окрашены лиловым цветом.
Картинка получена выбором параметров a = 1.8, и b = 0.2 i и поворотом на 900
Слайд 34МНОЖЕСТВО МАНДЕЛЬБРОТА (окрашено лиловым цветом). Картинка получается с помощью той же
процедуры, что и выше. Различие состоит в том, что начальное значение для точки z берётся всегда равным нулю, а точке с координатами (х; у) на картинке соответствует комплексный параметр b = x + y i.
Слайд 35
Это фракталы, при построении которых в итеративной системе случайным
образом изменяются какие-либо параметры.
Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.
Стохастические фракталы очень похожи на природные объекты – несимметричные деревья, изрезанные береговые линии.
Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.
Стохастические фракталы очень похожи на природные объекты – несимметричные деревья, изрезанные береговые линии.
СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ
Слайд 381. Проанализирована и проработана литература по теме исследования.
2. Рассмотрены и изучены
различные виды фракталов.
3. Представлена классификация фракталов.
4. Собрана коллекция фрактальных образов для первичного ознакомления с миром фракталов.
5. Составлены программы для построения графического образа фракталов.
3. Представлена классификация фракталов.
4. Собрана коллекция фрактальных образов для первичного ознакомления с миром фракталов.
5. Составлены программы для построения графического образа фракталов.
ЗАКЛЮЧЕНИЕ
Слайд 39«Фракталы - это глубокая философская идея, впервые позволившая связать традиции востока
и запада. К сожалению пока это жутко трудно понять, еще труднее объяснить».
неизвестный философ
неизвестный философ
Слайд 40Страница авторов: Власова Алина и Симонова Лариса Научный руководитель: учитель математики Приходько
Ю.В.
МОУ «Ржаницкая средняя
общеобразовательная школа"
с. Ржаница- 2011
