- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентационный материал по дисциплине Основы архитектуры, устройство и функционирование вычислительных систем
Содержание
- 1. Презентационный материал по дисциплине Основы архитектуры, устройство и функционирование вычислительных систем
- 2. Минимизация, или сокращение выражения, для ПФ необходима,
- 3. Для минимизации ПФ используют два основных метода: метод Квайна; метод карт Карно (диаграмм Вейча)
- 4. Метод Квайна применяется к функциям, заданным в
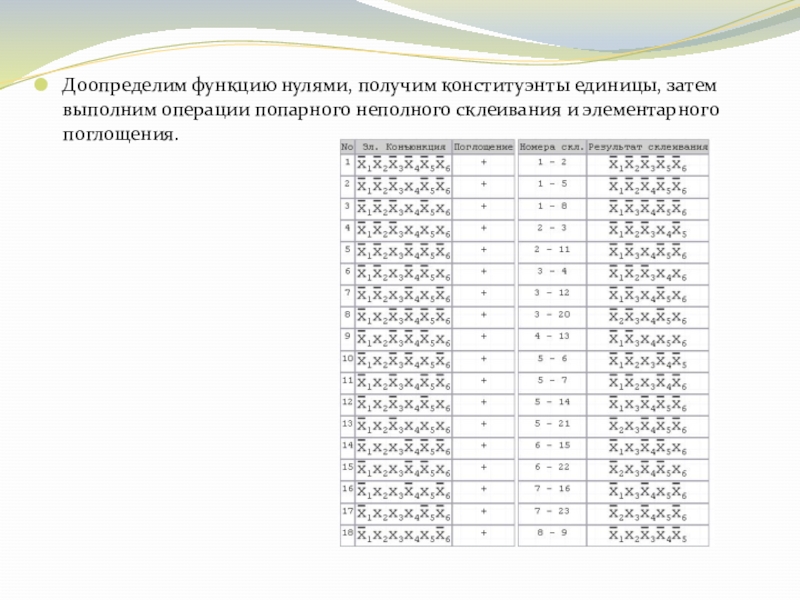
- 5. Доопределим функцию нулями, получим конституэнты единицы, затем выполним операции попарного неполного склеивания и элементарного поглощения.
- 6. Метод диаграмм Вейча (карт Карно) Метод диаграмм
- 7. Карта Карно — графический способ минимизации переключательных
- 8. Слайд 8
- 9. Принципы минимизацииОсновным методом минимизации логических функций, представленных
- 10. Слайд 10
- 11. В случае функции трёх переменных приходится иметь
- 12. Слайд 12
- 13. Слайд 13
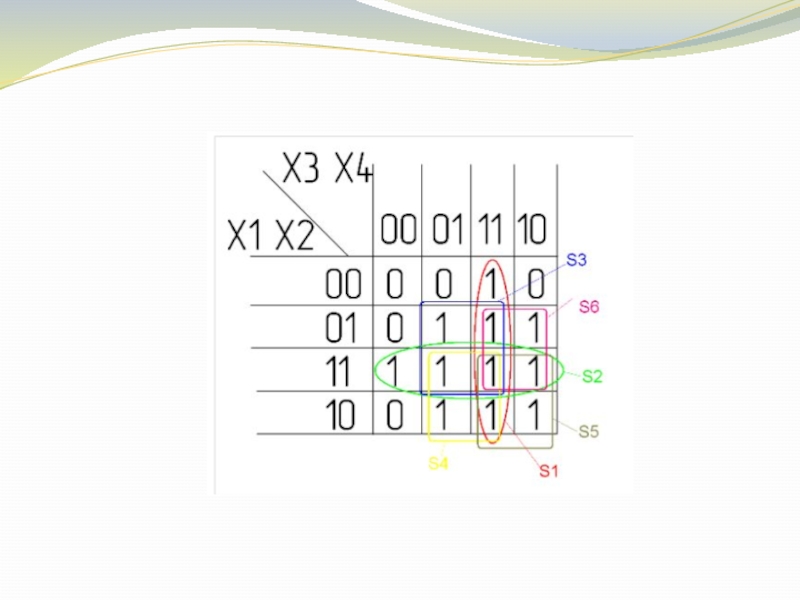
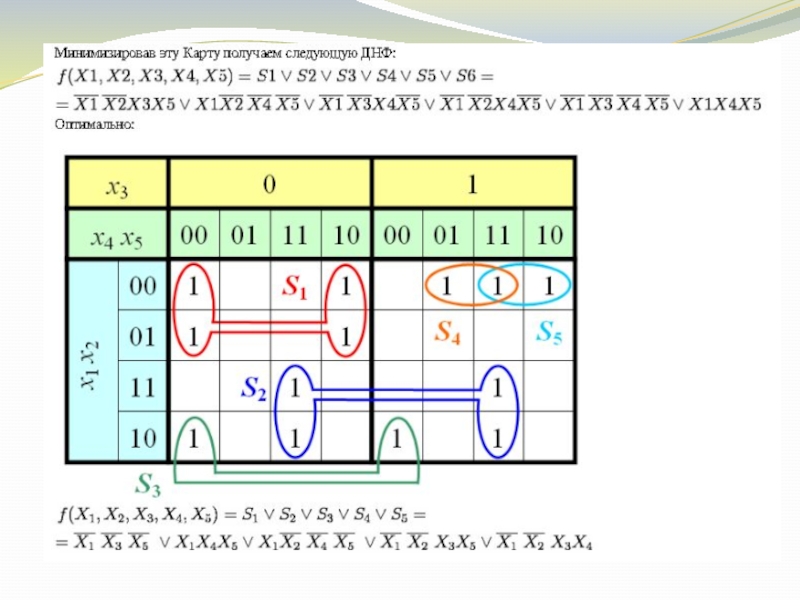
- 14. Пример Карты Карно на пять переменных
- 15. Слайд 15
Минимизация, или сокращение выражения, для ПФ необходима, чтобы обеспечить минимум затрат оборудования при построении функциональной схемы в заданном базисе (наборе) логических элементов. Чаще всего используется набор И, ИЛИ, НЕ, а минимизация ПФ ведется в ДНФ. В
Слайд 2Минимизация, или сокращение выражения, для ПФ необходима, чтобы обеспечить минимум затрат
оборудования при построении функциональной схемы в заданном базисе (наборе) логических элементов. Чаще всего используется набор И, ИЛИ, НЕ, а минимизация ПФ ведется в ДНФ. В рамках нормальных форм минимальной будет такая разновидность функции, которая состоит из наименьшего количества дизъюнктивных (конъюнктивных) членов при наименьшем суммарном числе символов переменных. В случае ДНФ в результате минимизации получается минимальная ДНФ (МДНФ).
Слайд 3Для минимизации ПФ используют два основных метода:
метод Квайна;
метод
карт Карно (диаграмм Вейча)
Слайд 4Метод Квайна применяется к функциям, заданным в СДНФ (возможно задание и
в СКНФ), и проводится в два этапа.
На первом этапе выполняется переход от СДНФ к сокращенной ДНФ путем проведения всех возможных склеиваний друг с другом сначала конъюнкций ранга п, затем ранга n — 1, далее n — 2 и т. д.
На первом этапе выполняется переход от СДНФ к сокращенной ДНФ путем проведения всех возможных склеиваний друг с другом сначала конъюнкций ранга п, затем ранга n — 1, далее n — 2 и т. д.
Слайд 5Доопределим функцию нулями, получим конституэнты единицы, затем выполним операции попарного неполного
склеивания и элементарного поглощения.
Слайд 6Метод диаграмм Вейча (карт Карно)
Метод диаграмм Вейча (карт Карно) удобен
для минимизации ПФ, содержащих обычно не более четырех переменных.
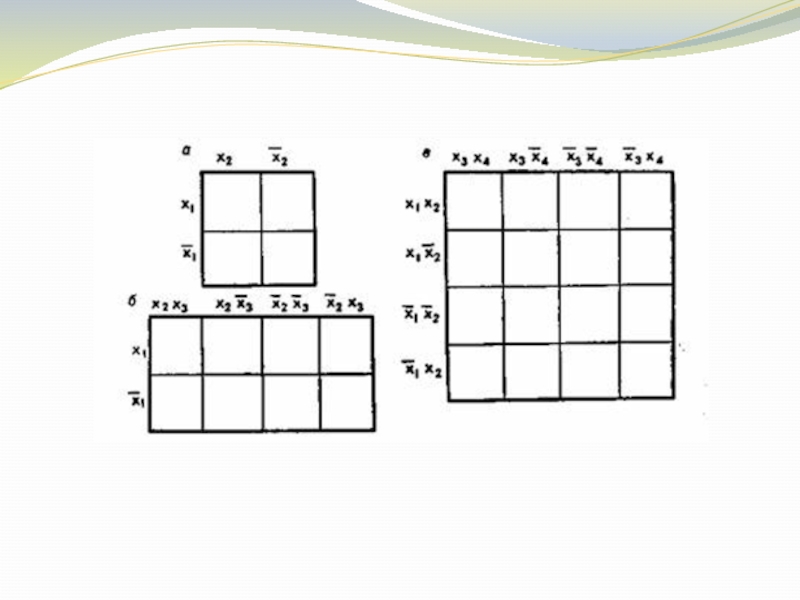
Диаграмма Вейча имеет вид прямоугольника (квадрата), разбитого на 2n клеток, где n — число аргументов ПФ. Каждой клетке диаграммы ставится в соответствие определенная конъюнкция, причем конъюнкции располагают таким образом, чтобы в соседних клетках (в строке или в столбце) они отличались не более чем значением одной переменной. В результате любые две соседние в строке или в столбце конъюнкции склеиваются но соответствующей переменной. Соседними на диаграмме являются также крайние (левая и правая) конъюнкции в одной строке и (нижняя и верхняя) конъюнкции в одном столбце.
Диаграмма Вейча имеет вид прямоугольника (квадрата), разбитого на 2n клеток, где n — число аргументов ПФ. Каждой клетке диаграммы ставится в соответствие определенная конъюнкция, причем конъюнкции располагают таким образом, чтобы в соседних клетках (в строке или в столбце) они отличались не более чем значением одной переменной. В результате любые две соседние в строке или в столбце конъюнкции склеиваются но соответствующей переменной. Соседними на диаграмме являются также крайние (левая и правая) конъюнкции в одной строке и (нижняя и верхняя) конъюнкции в одном столбце.
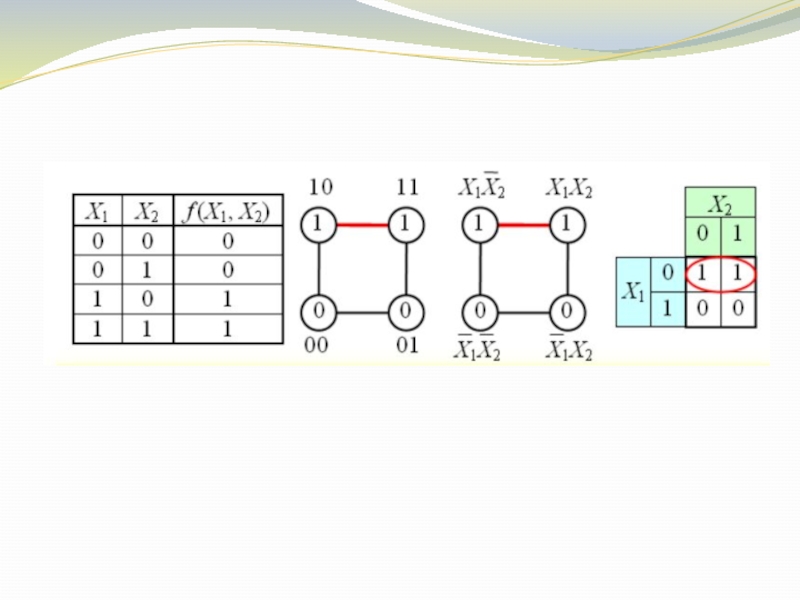
Слайд 7Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную
простоту работы с большими выражениями и устранение потенциальных гонок.
Представляет собой операции попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба
Представляет собой операции попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба
Слайд 9Принципы минимизации
Основным методом минимизации логических функций, представленных в виде СДНФ или
СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.
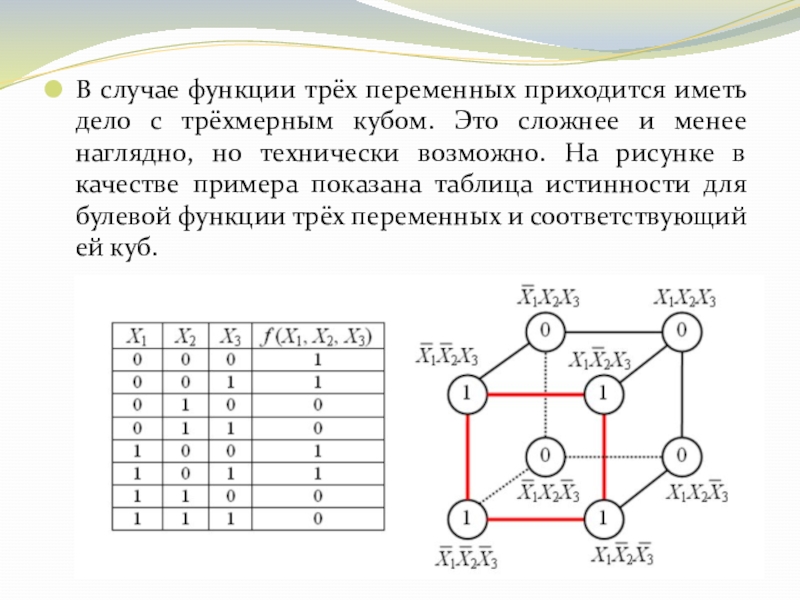
Слайд 11В случае функции трёх переменных приходится иметь дело с трёхмерным кубом.
Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.