- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок по технической механике на тему Растяжение - сжатие
Содержание
- 1. Открытый урок по технической механике на тему Растяжение - сжатие
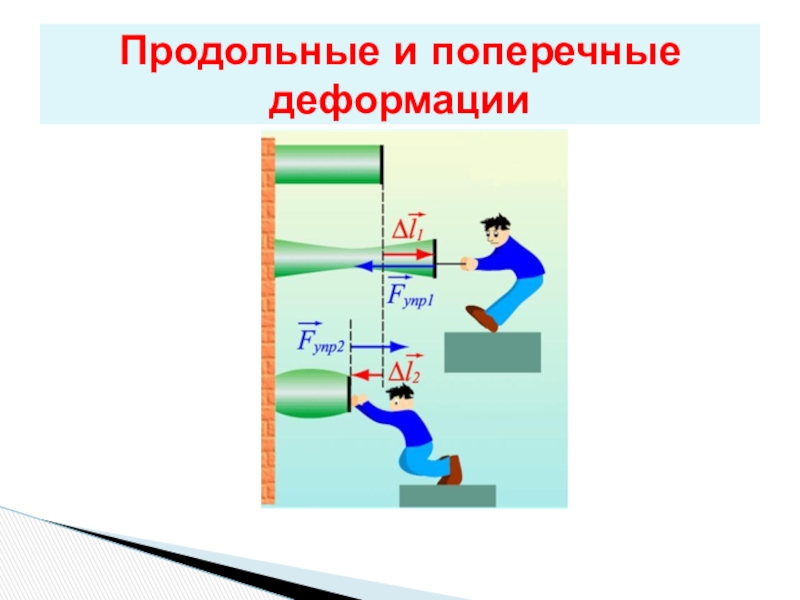
- 2. Продольные и поперечные деформации
- 3. Рассмотрим деформацию бруса под действием продольной силы
- 4. В сопротивлении материалов принято рассчитывать деформации в
- 5. Между продольной и поперечной деформацией существует зависимость/
- 6. ПУАССОН (Poisson) Симеон ДениДата рождения:21 июня 1781Дата смерти: 25 апреля 1840
- 7. Закон ГукаГук (Хук) (Hooke) Роберт ,1635 – 1703 гг.
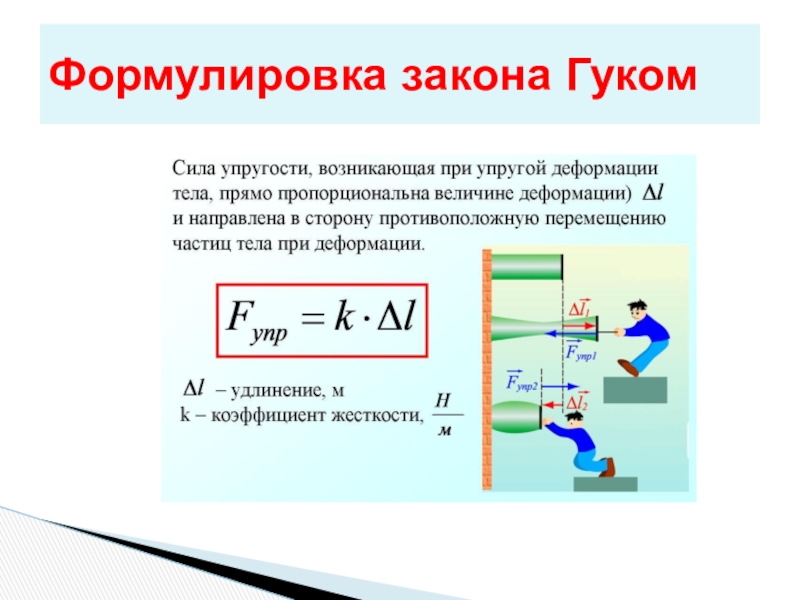
- 8. Формулировка закона Гуком
- 9. Модуль упругостиk (коэффициент жесткости) зависит как от
- 10. Томас Юнг Thomas YoungДата рождения: 13 июня 1773Дата смерти: 10 мая 1829 (55 лет)
- 11. В пределах упругости нормальные напряжения пропорциональны относительному
- 12. Закон Гука σ = Е,
- 13. 1. Абсолютное удлинение бруса прямо пропорционально
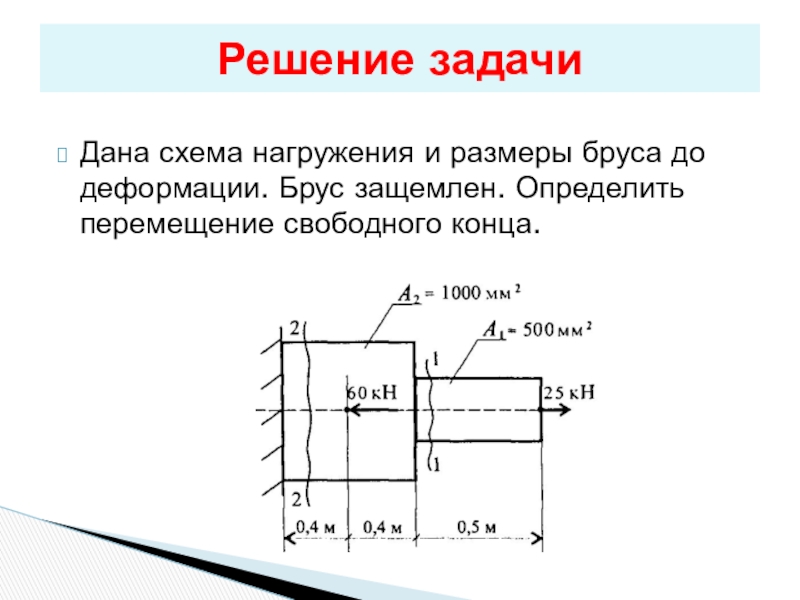
- 14. Дана схема нагружения и размеры бруса до деформации. Брус защемлен. Определить перемещение свободного конца.Решение задачи
- 15. 1. Брус ступенчатый, поэтому следует построить эпюры
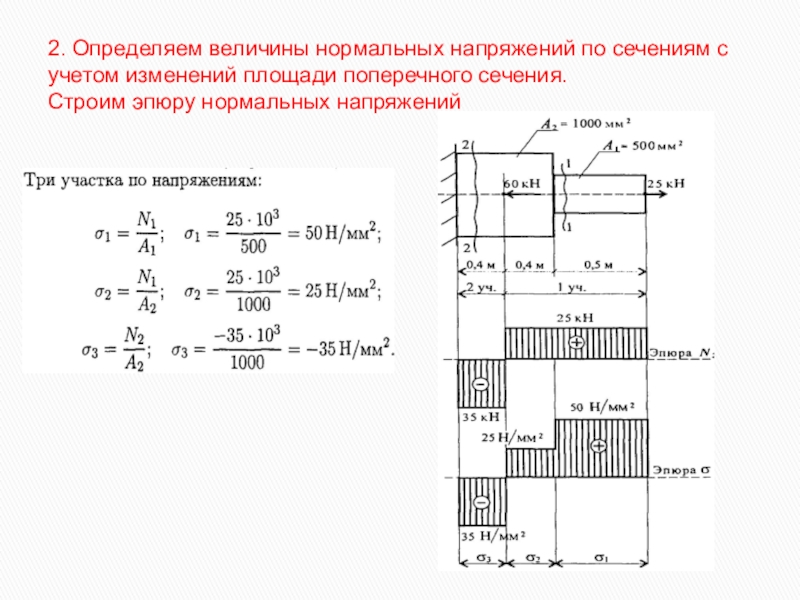
- 16. 2. Определяем величины нормальных напряжений по сечениям
- 17. 3. На каждом участке определяем абсолютное удлинение. Результаты алгебраически суммируем.
- 18. Контрольные вопросы 1.
Слайд 1Занятие 30
Растяжение и сжатие
Продольные и поперечные деформации
Коэффициент Пуассона
Закон Гука
Определение осевых перемещений
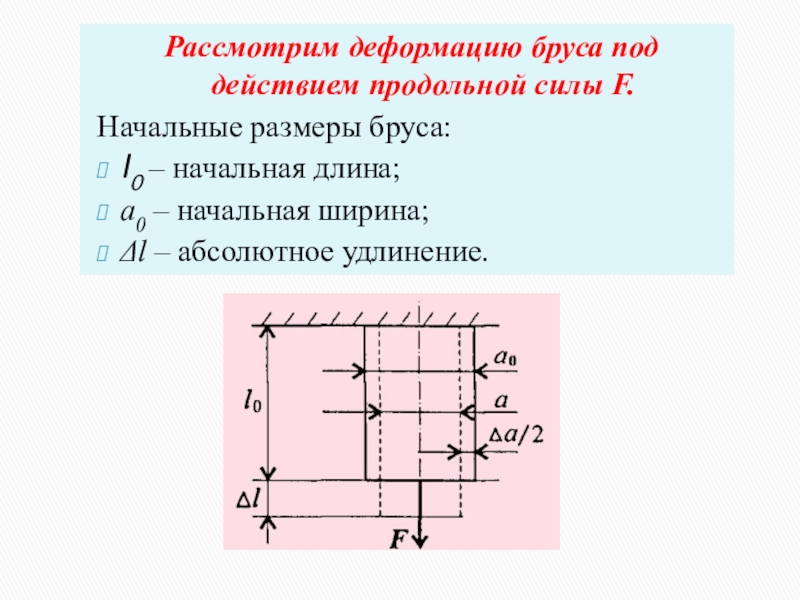
Слайд 3Рассмотрим деформацию бруса под действием продольной силы F.
Начальные размеры бруса:
l0 –
a0 – начальная ширина;
l – абсолютное удлинение.
Слайд 4В сопротивлении материалов принято рассчитывать деформации в относительных единицах:
=l /
‑ относительное удлинение (продольная деформация)
/ =а /а0,
/‑ относительное сужение (поперечная деформация)
Относительные деформации
Слайд 5Между продольной и поперечной деформацией существует зависимость
/ = ,
где ‑
Относительные деформации
Слайд 9Модуль упругости
k (коэффициент жесткости) зависит как от свойств материала, так и
, откуда
Величина Е называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
Слайд 11
В пределах упругости нормальные напряжения пропорциональны относительному удлинению.
Значение Е для сталей
Вывод закона Гука в современной форме
Слайд 12Закон Гука σ = Е, откуда
= σ/Е
Относительное
= ∆l / l0
Приравняем правые части выражений (учтем, что σ=N/А) и получим
σ/Е = ∆l / l0
∆l = σl0/Е или
∆l = Nl0 /АЕ,
где ∆l – абсолютное удлинение, мм;
σ – нормальное напряжение, МПа;
l0 – начальная длина, мм;
Е – модуль упругости материала, МПа;
А – площадь поперечного сечения, мм2.
Произведение АЕ называют жесткостью сечения.
Формулы для расчета перемещений при растяжении и сжатии
Слайд 13 1. Абсолютное удлинение бруса прямо пропорционально величине продольной силы в сечении,
ВЫВОДЫ
Слайд 14Дана схема нагружения и размеры бруса до деформации. Брус защемлен. Определить
Решение задачи
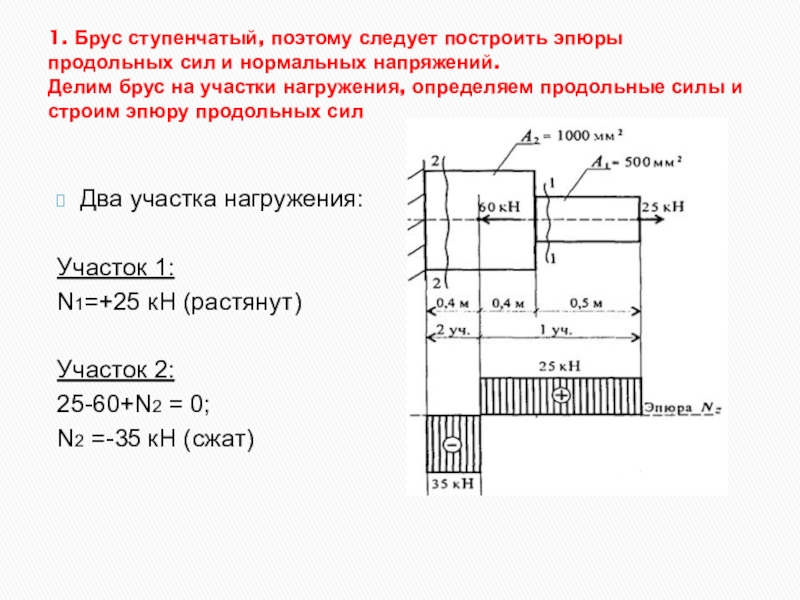
Слайд 151. Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных
Два участка нагружения:
Участок 1:
N1=+25 кН (растянут)
Участок 2:
25-60+N2 = 0;
N2 =-35 кН (сжат)