- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему НПК Задачи на дополнительное построение
Содержание
- 1. НПК Задачи на дополнительное построение
- 2. Цель работы: выделить основные виды дополнительных построений,
- 3. Продолжить медиануДано:
- 4. №2. На сторонах AB и BC
- 5. Слайд 5
- 6. Провести прямую параллельную даннойДано:ABCD− равнобедренная трапецияAC и
- 7. №2 Через середину M стороны BC
- 8. №1 На
- 9. №2 Пусть AC − большая из диагоналей
- 10. Дано пятиконечная звезда
- 11. №1 В трапеции ABCD
- 12. Заключение Рассмотрев конкретные случаи, мы убедились,
Слайд 1Задачи на дополнительное построение
Работу выполнил:
Абдюшев Никита, ученик 8б класса
МОБУ СОШ
Руководитель: Кабирова Л. Ф.
Слайд 2Цель работы: выделить основные виды дополнительных построений, к каждому виду подобрать
Задачи:
– Изучить статьи, газеты, журналы и задачники
– Выделить основные виды дополнительных построений
– Подобрать задачи к выделенным видам, решаемые с помощью дополнительных построений
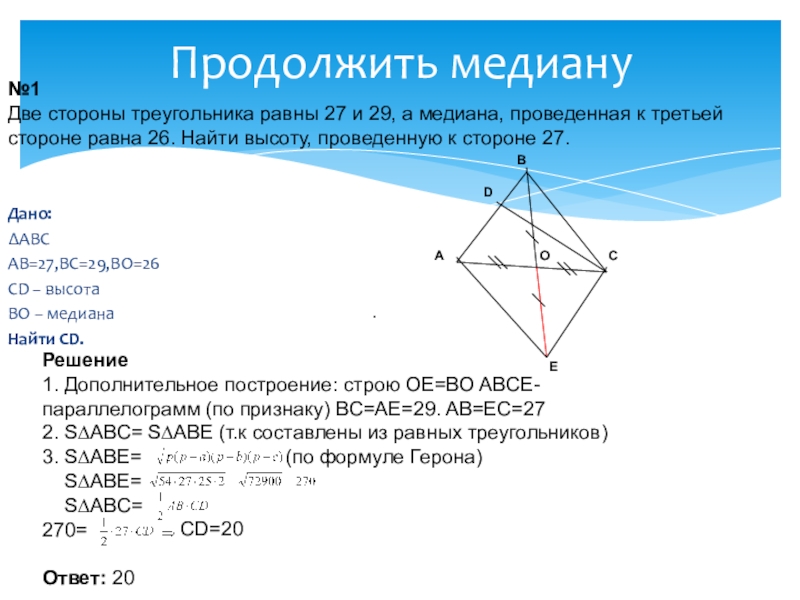
Слайд 3Продолжить медиану
Дано:
∆ABC
AB=27,BC=29,BO=26
CD − высота
BO − медиана
Найти CD.
.
B
D
A O C
E
№1
Две стороны треугольника равны 27 и 29, а медиана, проведенная к третьей
стороне равна 26. Найти высоту, проведенную к стороне 27.
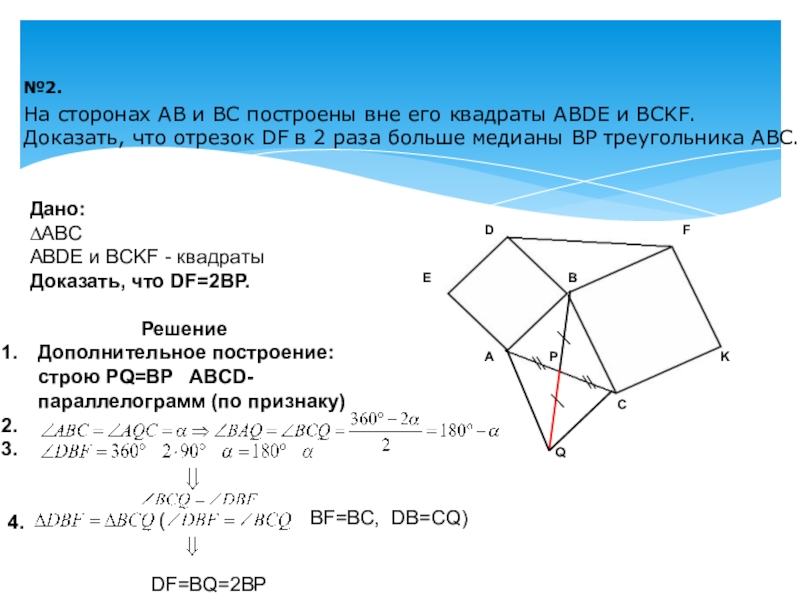
Слайд 4№2.
На сторонах AB и BC построены вне его квадраты
Дано:
∆ABC
ABDE и BCKF - квадраты
Доказать, что DF=2BP.
D F
E B
A P K
C
Q
Слайд 5
1.Дополнительное построение: строю PD=BPABCD-
параллелограмм (по признаку) AB=CD, BC=AD
2. BD
BD
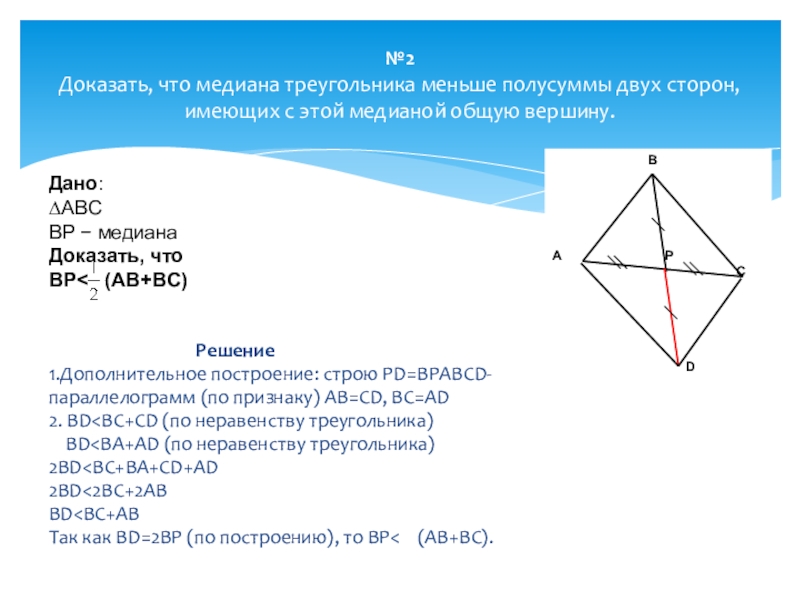
№2
Доказать, что медиана треугольника меньше полусуммы двух сторон, имеющих с этой медианой общую вершину.
Дано:
∆ABC
BP − медиана
Доказать, что BP< (AB+BC)
B
A P
C
D
Слайд 6Провести прямую параллельную данной
Дано:
ABCD− равнобедренная трапеция
AC и BD − диагонали
AC
S − площадь трапеции
Найти h − высоту трапеции
B C
A F D E
№1
Найти высоту равнобедренной трапеции, если её диагонали взаимно перпендикулярны, а площадь трапеции равна S.
Слайд 7№2 Через середину M стороны BC параллелограмма ABCD, площадь которого равна
Дано:
ABCD−параллелограмм
SABCD=1
BM=MC
Найти площадь OMCD.
B M C
O
F
E A D
Слайд 8 №1
На катетах AC и BC
Провести прямую перпендикулярную данной
K
D
C
E F
P
M
A
L
B N Q
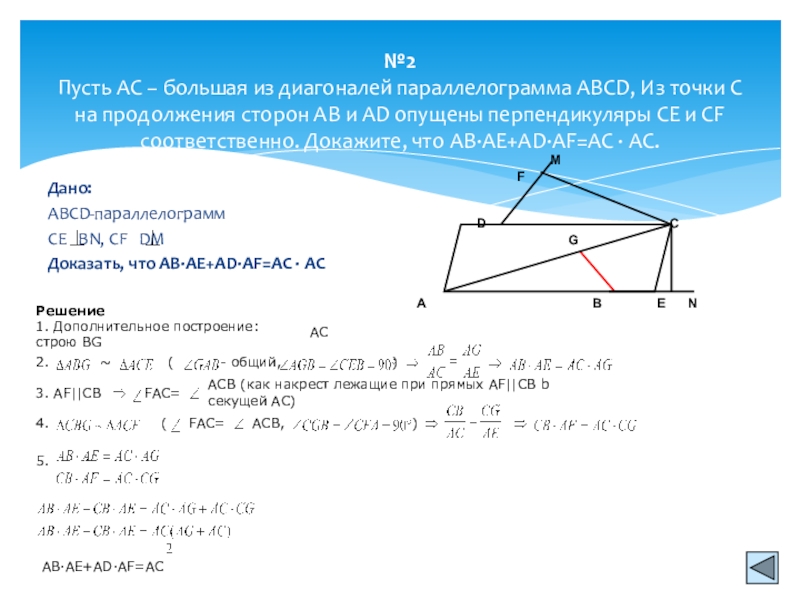
Слайд 9№2 Пусть AC − большая из диагоналей параллелограмма ABCD, Из точки C
Дано:
ABCD-параллелограмм
CE BN, CF DM
Доказать, что AB∙AE+AD∙AF=AC ∙ AC
M
F
D C
G
A B E N
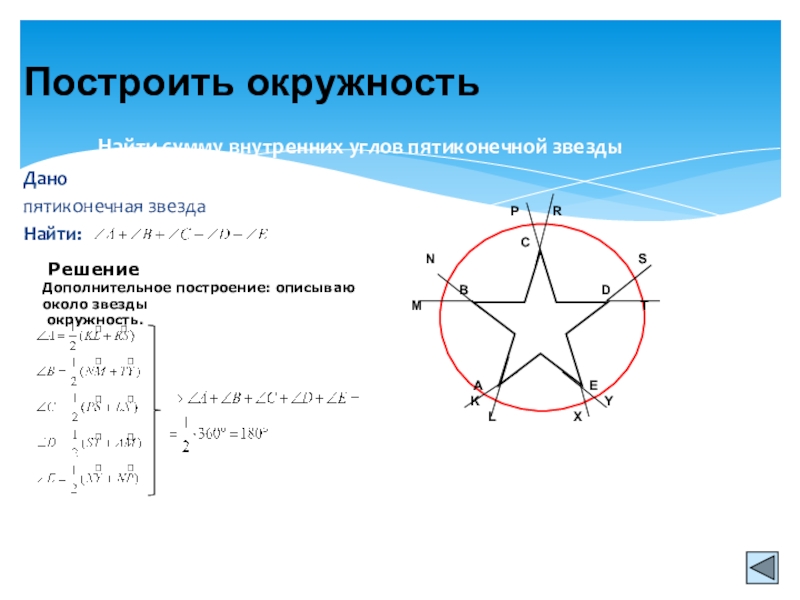
Слайд 10Дано
пятиконечная звезда
Найти:
Найти сумму внутренних углов пятиконечной звезды
P R
C
N S
B D
M T
A E
K Y
L X
Построить окружность
Слайд 11№1 В трапеции ABCD (AB и CD основания) меньшее
Дано:
ABCD – трапеция
AB и CD -основания
Найти S трапеции.
B C
Q
O
A D