- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Межпредметные понятия и формирование УУД при изучении математики
Содержание
- 1. Межпредметные понятия и формирование УУД при изучении математики
- 2. МБОУ «ЗЕЛЕНЕЦКАЯ СОШ»МЕЖПРЕДМЕТНЫЕ ПОНЯТИЯ И
- 3. Какие понятия считать межпредметными и в чем особенностьих изучения на уроках математики?«корень»«корень уравнения»«корень слова»
- 4. Нет четкого определения межпредметных понятий.В школьной математике
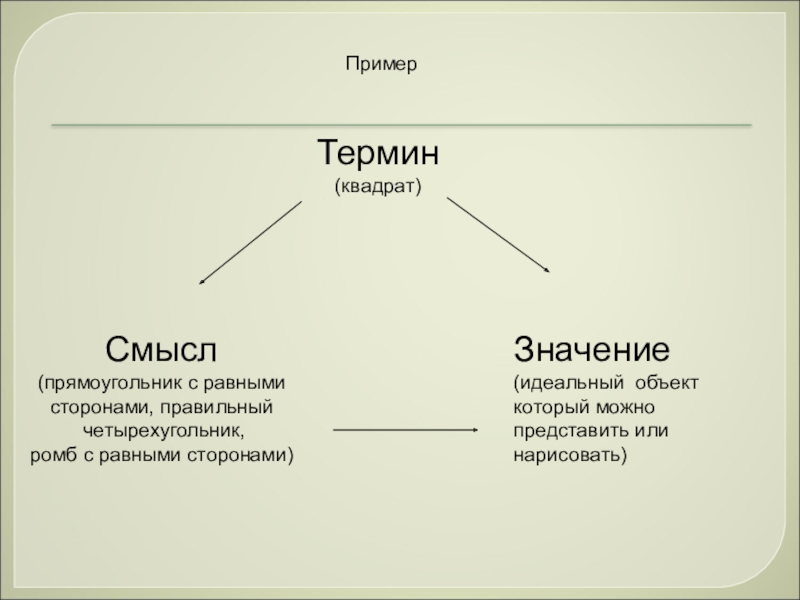
- 5. Термин (квадрат)Значение(идеальный объекткоторый можно представить или нарисовать)Смысл(прямоугольник с равными сторонами, правильный четырехугольник,ромб с равными сторонами)Пример
- 6. Примеры соподчиненных понятий« кровеносная система »«система уравнений»«
- 7. A - система (как межпредметное понятие)В -
- 8. Примеры«числовая функция»«функции государственных органов»Свойства специфические:В математике: функция-это
- 9. Наличие специфических свойств делает понятия, подчиненные межпредметным, трудными в усвоении. УУД –рефлексия деятельностиКакие УУД формируются?
- 10. Этапы формирования межпредметных и подчиненных им понятийс
- 11. Примеры межпредметных понятий функциякругкоординатыкореньотношениеНа уроках математики
- 12. вывод Систематическая работа с такими
- 13. Примеры реализации межпредметных связейЗадача. Вычислить, сколько нужно
- 14. Знания, которые мы научились применять на уроке,
- 15. 6 классе ( математика + медицина)Тема: «Процент»Задача
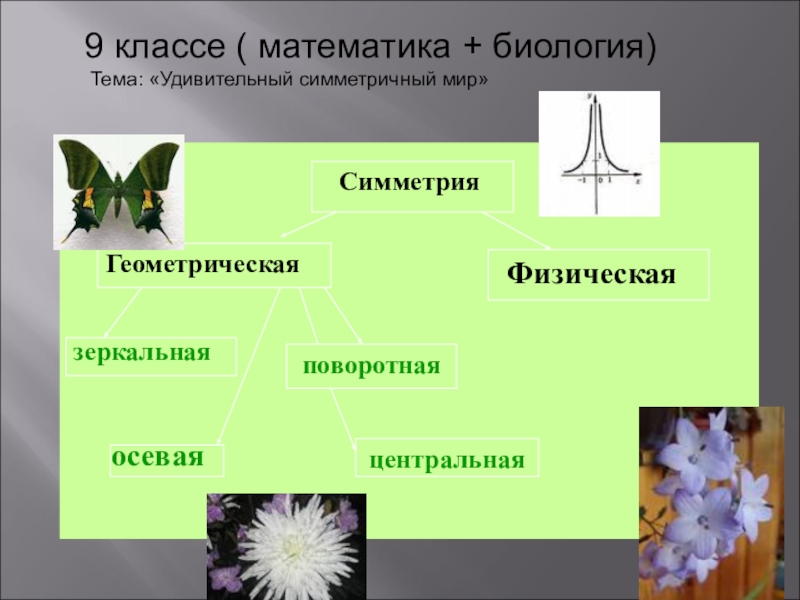
- 16. СимметрияГеометрическаяФизическаязеркальнаяповоротнаяосеваяцентральная9 классе ( математика + биология) Тема: «Удивительный симметричный мир»
- 17. Спасибо за ВНИМАНИЕ
Слайд 1
"Когда приступают к изучению какого-либо предмета, умы учеников должны быть к
Слайд 2
МБОУ «ЗЕЛЕНЕЦКАЯ СОШ»
МЕЖПРЕДМЕТНЫЕ ПОНЯТИЯ И
ФОРМИРОВАНИЕ
ПРИ ИЗУЧЕНИИ МАТЕМАТИКИ
учитель математики Попова Л. Б.
2015-2016 учебный год
Слайд 3
Какие понятия считать межпредметными и в чем особенность
их изучения на уроках
«корень»
«корень уравнения»
«корень слова»
Слайд 4
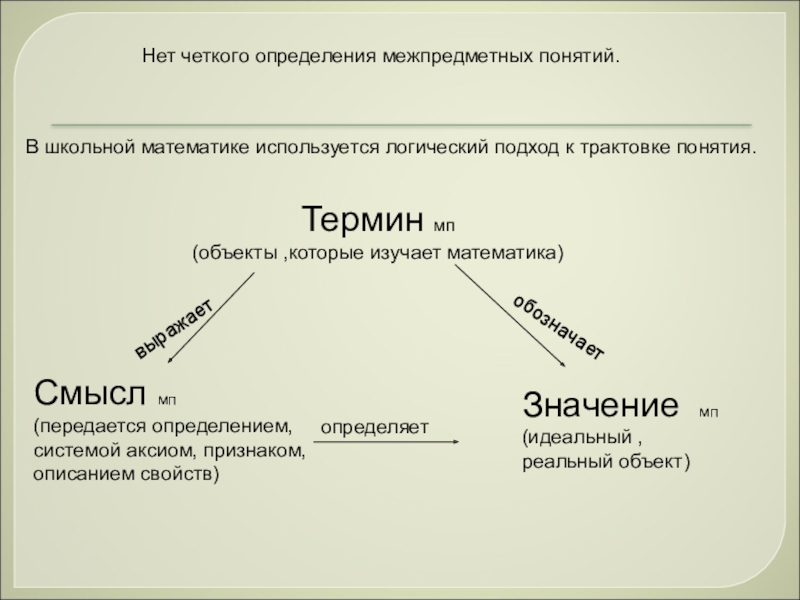
Нет четкого определения межпредметных понятий.
В школьной математике используется логический подход к
Термин мп
(объекты ,которые изучает математика)
Значение мп
(идеальный ,
реальный объект)
Смысл мп
(передается определением,
системой аксиом, признаком,
описанием свойств)
выражает
обозначает
определяет
Слайд 5
Термин
(квадрат)
Значение
(идеальный объект
который можно представить или нарисовать)
Смысл
(прямоугольник с равными
сторонами, правильный
ромб с равными сторонами)
Пример
Слайд 6
Примеры соподчиненных понятий
« кровеносная система »
«система уравнений»
« солнечная система»
Свойства общие:
рассматривается множество
объекты находятся в отношениях и связях друг с другом;
образуют определенную целостность;
Вывод: совокупность этих свойств представляет с логической точки зрения
межпредметное понятие
Целью изучения на разных предметах
является формирование межпредметных
и подчиненных им понятий
Слайд 7
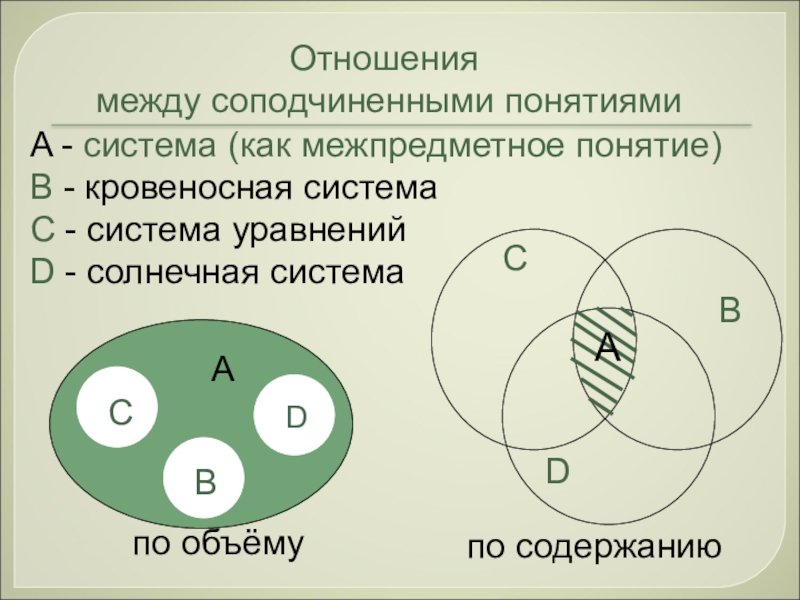
A - система (как межпредметное понятие)
В - кровеносная система
С -
D - солнечная система
В
В
C
D
A
Отношения
между соподчиненными понятиями
по объёму
по содержанию
С
В
D
А
Слайд 8
Примеры
«числовая функция»
«функции государственных органов»
Свойства специфические:
В математике: функция-это соответствие между элементами двух
при этом каждому элементу одного множества соответствует единственный
элемент другого множества.
Под функцией госорганов понимаются их конкретные полномочия.
И здесь тоже можно выделить два множества: множество органов (законодательные) и множество полномочий органов.
«функция членов предложения»
«функция легких», «функции родителей»
« функции телефона»
Свойства общие:
заданы два множества;
установлено соответствие между элементами этих множеств;
Слайд 9
Наличие специфических свойств делает понятия, подчиненные межпредметным, трудными в усвоении.
УУД
Какие УУД формируются?
Слайд 10
Этапы формирования межпредметных и подчиненных им понятий
с точки зрения формирования познавательных
1 этап
Выявление субъективного опыта учащихся
(формирование личностного УУД, как смыслообразование);
2 этап
Формирование обобщенного представления (предпонятие) о межпредметном понятии
(формирование познавательного УУД – умение выделять свойства);
3 этап
Формирование понятия, подчиненного межпредметному
(формирование познавательного УУД - умение относить объект к понятию и умение определять понятие);
Слайд 12
вывод
Систематическая работа с такими понятиями, включающая реализацию на
Слайд 13Примеры реализации межпредметных связей
Задача. Вычислить, сколько нужно вырубить леса для того,
Решение:
Размеры одной страницы учебника 14см на 21 см, т.е. площадь равна14 см* 21 см=294 см
В учебнике 384 страниц или 192 листа, значит площадь всех листов учебника 294 см² ∙192 лис.=156448 см²= 5м² 6448 см² На 1000 м2 нужно вырубить ¼ га=2500 м2 деревьев, т.е. в 2,5 раза больше. Значит на производство одного учебника требуется 5м² 6448 см² ∙2,5= 14м²1120 см² леса
На весь тираж в 100000 экземпляров требуется:
леса, а это примерно 14 га
Ответ: 14 га
141120 см² ∙100000=14112000000 см² =141120 м²
8 класс ( математика + экология)
Слайд 14Знания, которые мы научились применять на уроке, появились несколько тысячелетий назад,
11 класс ( математика + история)
Слайд 156 классе ( математика + медицина)
Тема: «Процент»
Задача . Определение пропорциональности своего
ХОД РАБОТЫ
- Измерьте свой рост или рост своего друга стоя;
- Измерьте свой рост или рост своего друга сидя;
- Воспользовавшись формулой:
где А — показатель пропорциональности телосложения, оцените
пропорциональность физического развития по следующей таблице: