- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Как подобие используется на практике
Содержание
- 1. Как подобие используется на практике
- 2. Геометрия – это не просто наука о
- 3. ГипотезаВозможно ли применение подобия в практических целях?
- 4. Цели и задачи проекта.Узнать:Где можно встретить подобие.Как подобие используют на практике.
- 5. Содержание:Тема 1:Что такое подобные фигуры ?Тема 2:Зачем
- 6. ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы
- 7. Слайд 7
- 8. Тема2: Зачем применяют подобие.Подобие применяют для того чтобы создавать макеты удобные по размеру.
- 9. Тема3: примеры подобных фигур в повседневной жизни.Автомобиль т его модель подобные тела.
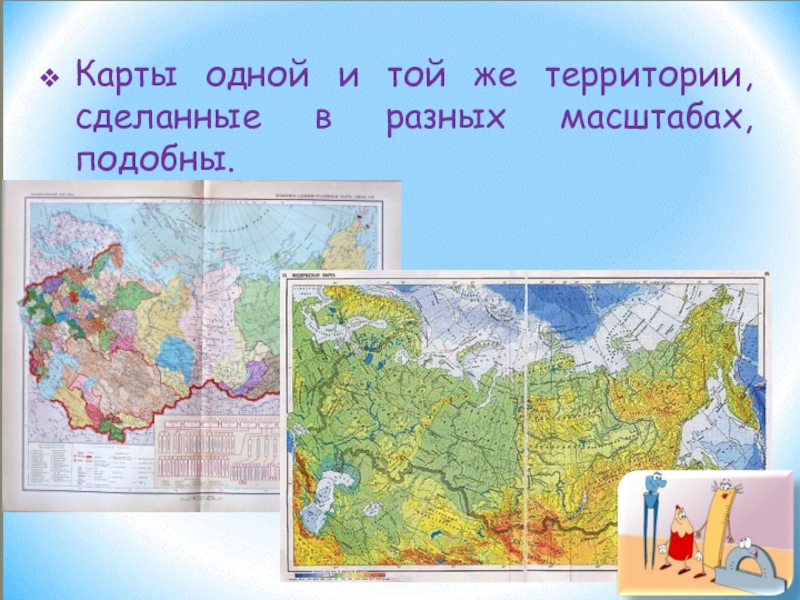
- 10. Карты одной и той же территории, сделанные в разных масштабах, подобны.
- 11. картина и её фотография — это подобные фигуры.
- 12. Египетские пирамиды подобны друг другу, также любой
- 13. Правило золотого сечения.Принцип золотого сечения – высшеепроявление
- 14. Портрет Монны Лизы (Джоконды) долгие годы
- 15. В этой картине фигура Пушкина также
- 16. Рассмотрим побег цикория. От основного стебля образовался
- 17. У многих бабочек соотношение размеров грудной и
- 18. И. Шевелев, изучая архитектуру церкви Покрова на
- 19. Тема8: Что такое подобные треугольники?Подобные треугольники —
- 20. Слайд 20
- 21. Зная признаки подобия треугольников, можно определить высоту какого-либо предмета или рассчитать расстояние до недоступной точки.
- 22. Самый лёгкий и самый древний
- 23. Слайд 23
- 24. Тема10: Измерение расстояния до недоступно точки.Для нахождения
- 25. Слайд 25
- 26. Вот как этот способ пригодился старшему сержанту
- 27. Слайд 27
- 28. Решение задачи.Способ этот состоит в следующем. Надо
- 29. ВыводТаким образом, признаки подобия фигур – одно
- 30. Слайд 30
Слайд 2Геометрия – это не просто наука о свойствах
геометрических фигур.
Геометрия –
нас с самого рождения.
Ведь все, что мы видим вокруг, так или иначе
относится к геометрии, ничто не ускользает от
ее внимательного взгляда. Геометрия помогает
человеку идти по миру с широко открытыми
глазами, учит внимательно смотреть вокруг и
видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.
Вступление
Слайд 5Содержание:
Тема 1:Что такое подобные фигуры ?
Тема 2:Зачем применяют подобие?
Тема 3:Примеры подобных
Тема 4: Правило Золотого сечения.
Тема 5:Правило Золотого сечения в живописи.
Тема6:Правило Золотого сечения в природе.
Тема 7:Правило золотого сечения в архитектуре.
Тема 8:Что такое подобные треугольники?
Тема 9:Измерение высоты при помощи тени;
Тема 10:Измренение расстояния до недоступно точки;
Тема 11:Измерение расстояния при помощи «козырька»;
Слайд 6ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у геометрических фигур, независимо
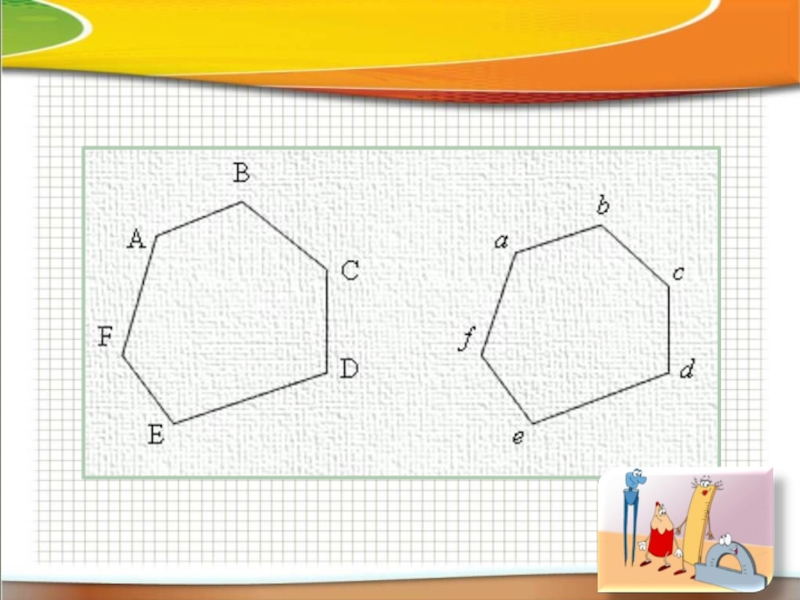
Тема1:
Что такое подобные фигуры?
Слайд 8Тема2:
Зачем применяют подобие.
Подобие применяют для того чтобы создавать макеты удобные по
Слайд 12Египетские пирамиды подобны друг другу, также любой макет подобен оригиналу, если
Слайд 13Правило золотого сечения.
Принцип золотого сечения – высшее
проявление структурного и функцио-
нального совершенства
частей в искусстве, науке, технике и
природе.
Золотое сечение – это такое пропорциональное деление отрезка
на неравные части, при котором весь отрезок так относится к большей
части, как сама большая часть относится к меньшей; или другими
словами, меньший отрезок так относится к большему, как больший
ко всему.
a:b=b:с или c: b=b:a
Тема 4.
Правило золотого сечения.
Слайд 14 Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые
являющихся частями правильного звездчатого пятиугольника.
Тема 5
Правило Золотого сечения в живописи.
Слайд 15 В этой картине фигура Пушкина также поставлена художником слева на
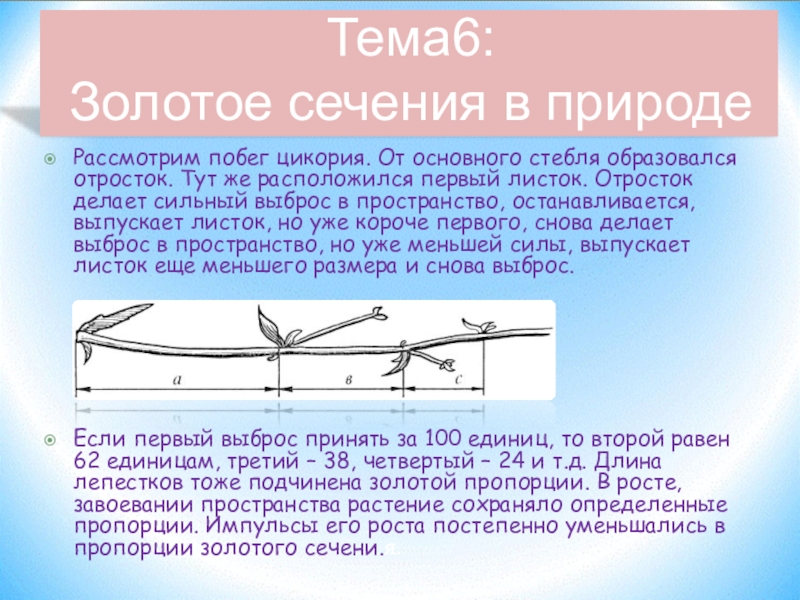
Слайд 16Рассмотрим побег цикория. От основного стебля образовался отросток. Тут же расположился
Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечени.я.
Тема6:
Золотое сечения в природе
Слайд 17У многих бабочек соотношение размеров грудной и брюшной части тела отвечает
Слайд 18И. Шевелев, изучая архитектуру церкви Покрова на Нерли, выяснил, что в
Тема7:
Золотое сечения в архитектуре.
Слайд 19Тема8:
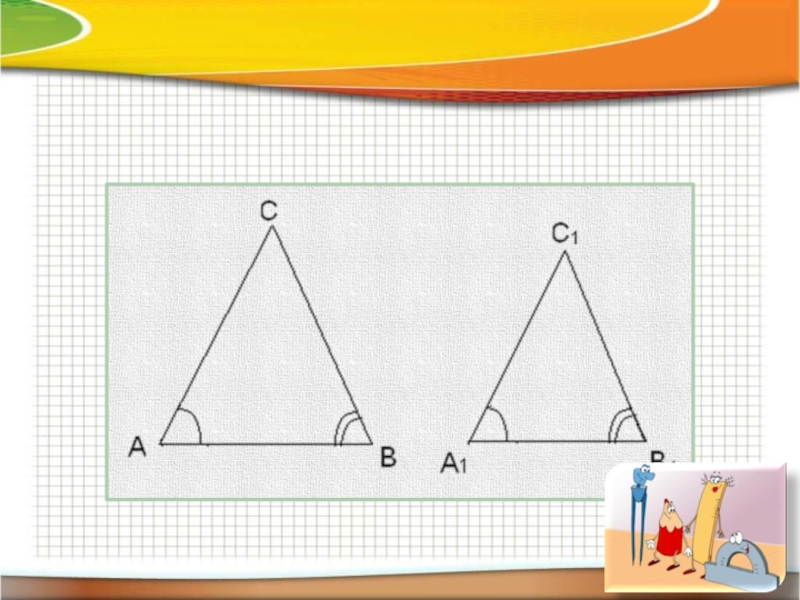
Что такое подобные треугольники?
Подобные треугольники — треугольники, у которых углы соответственно
Слайд 21Зная признаки подобия треугольников, можно определить высоту какого-либо предмета или рассчитать
Слайд 22
Самый лёгкий и самый древний способ – без сомнения, тот, которым
Тема9
Слайд 24Тема10:
Измерение расстояния до недоступно точки.
Для нахождения расстояния между двумя точками на
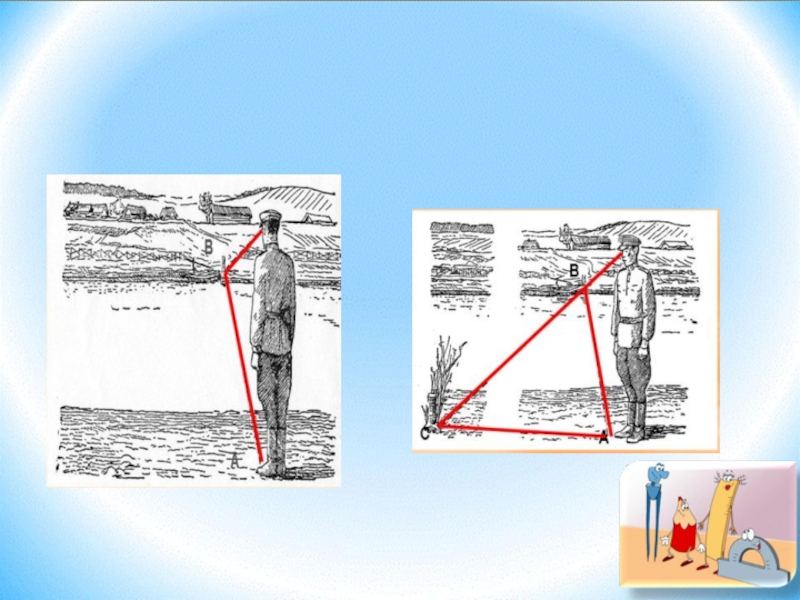
Слайд 26Вот как этот способ пригодился старшему сержанту Куприянову во фронтовой обстановке.
- Ну-ка, Карпов, сколько? - спросил Куприянов.
- По-моему, не больше 100-110 м,- ответил Карпов. Куприянов был согласен со своим разведчиком, но для контроля решил измерить ширину реки при помощи «козырька».
Тема 11:
Измерение расстояния при помощи «козырька».
Слайд 28Решение задачи.
Способ этот состоит в следующем. Надо стать лицом к реке
Расстояние до этой точки и будет примерно равно ширине реки.
Этим способом и воспользовался Куприянов. Он быстро встал в кустах, приложил ко лбу записную книжку, также быстро повернулся и завизировал дальнюю точку. Затем вместе с Карповым он ползком добрался до этой точки, измеряя расстояние шнуром. Получилось 105 м.