- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Электр тізбегінің эквивалентті түрленуі
Содержание
- 1. Электр тізбегінің эквивалентті түрленуі
- 2. ЖоспарКіріспеЭлектр тізбегінің элементтерінің тізбектей жалғануыЭлектр тізбегіндегі элементтердің
- 3. Тізбектей жалғану – бұл түйіні жоқ электр
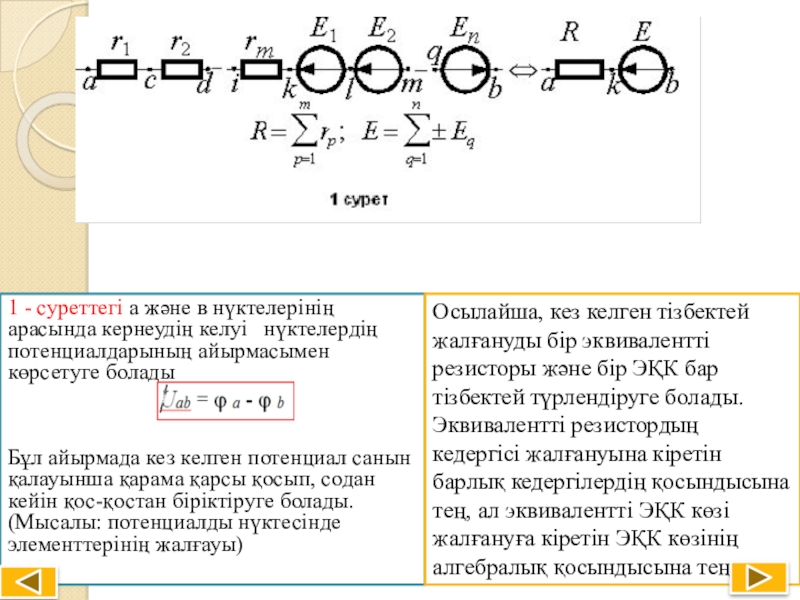
- 4. 1 - суреттегі а және в нүктелерінің
- 5. Тізбектей жалғанған элементтер коммутативті қасиетке ие, яғни
- 6. 1-есеп Параллель жалғанудың тізбектей жалғанудан ерекшелігі параллель
- 7. Параллель жалғанудың барлық элементтері екі түйінге байланысқан
- 8. Қорыта келгенде, әр түрлі саны бар элементтердің
- 9. Параллель жалғану кезінде бөлек элементтердің өткізгіштіктерінің қосындысы
- 10. Слайд 10
- 11. 2 - есеп Параллель жалғануға
- 12. 3-есеп3-шi суреттегі сұлба аралас қосылысқа жатады,
- 13. Слайд 13
- 14. Тізбектегі ажырау нүктелеріне қатысты кедергіні (кірістегі кедергі)
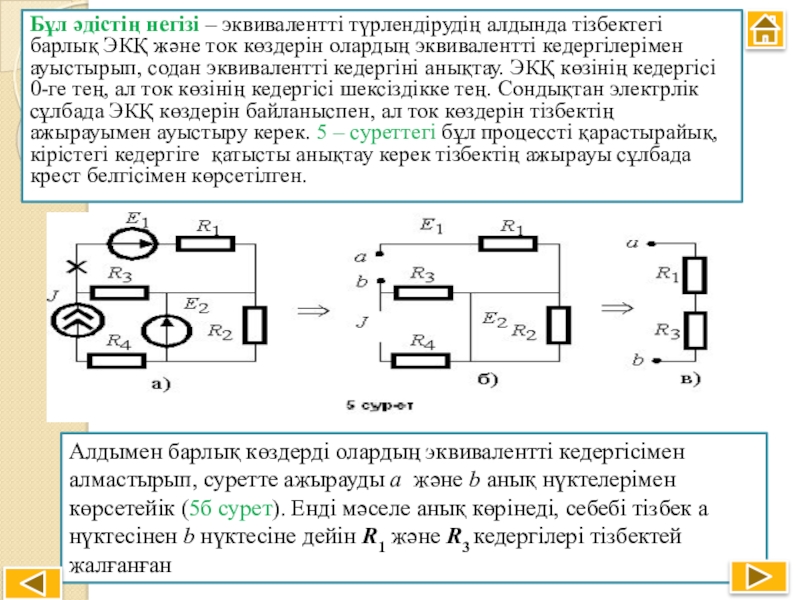
- 15. Бұл әдістің негізі – эквивалентті түрлендірудің алдында
- 16. 2.1 – суретте кедергілері тізбектей
- 17. Кихгофтың екінші заңына сәйкес электр тізбегінің кірісіндегі
- 18. 2.2 суреттегі электр тізбектегі кедергілердің параллель жалғануы
- 19. Кирхгофтың бірінші заңына сәйкес, сызбадағы тармақталмаған бөліктегі
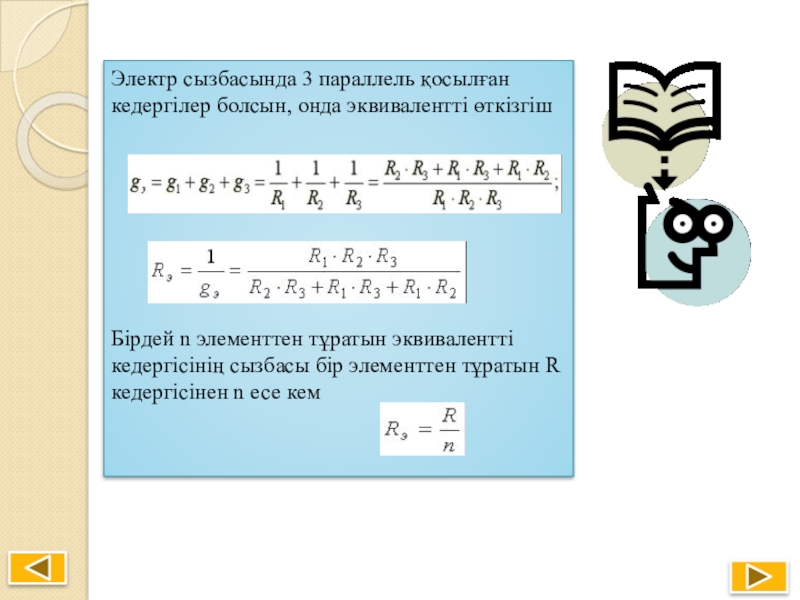
- 20. Электр сызбасында 3 параллель қосылған кедергілер болсын,
- 21. Екі параллель қосылған кедергілерден тұратын сызбаны (сурет
- 22. Параллель тармақтарындағы токтар Осыған ұқсас Параллель
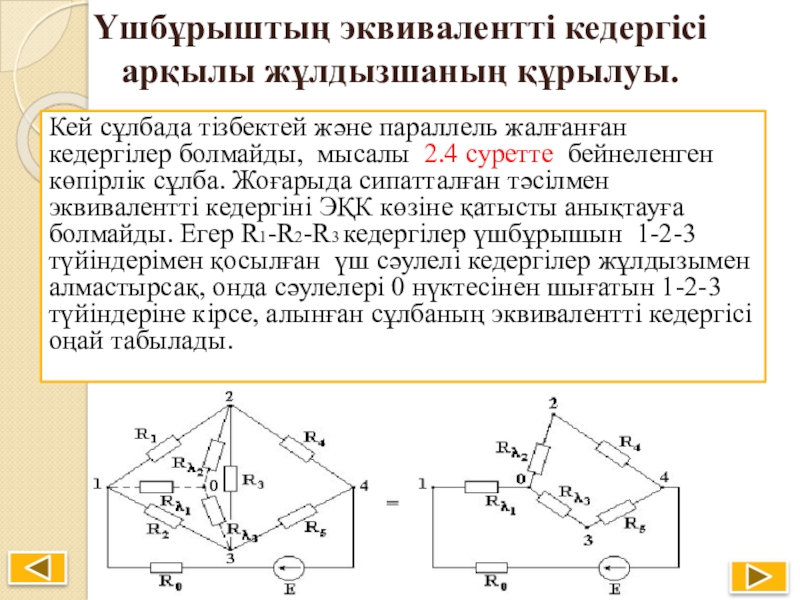
- 23. Үшбұрыштың эквивалентті кедергісі арқылы жұлдызшаның құрылуы.Кей сұлбада
- 24. Эквивалентті кедергілер жұлдызы сәулесіннің кедергісі үшбұрыштың іргелес
- 25. Жұлдызша кедергісінің эквивалентті үшбұрышқа айналуыСызбаның жеңілдету үшін
- 26. Кедергiлер жұлдызының эквивалентті үшбұрышқа өзгертуiЭквивалентті үшбұрыш кедергілерінің
Слайд 2Жоспар
Кіріспе
Электр тізбегінің элементтерінің тізбектей жалғануы
Электр тізбегіндегі элементтердің параллель жалғануы
Үшбұрыштың эквивалентті
Жұлдызша кедергісінің эквивалентті үшбұрышқа айналуы.
Кедергiлер жұлдызының эквивалентті үшбұрышқа өзгертуi
Слайд 3Тізбектей жалғану – бұл түйіні жоқ электр тізбегінің байланысқан элементтерінің жиынтығы.
Тізбектей жалғауының жалпы жағдайында ЭҚК көзі және резисторларының кез келген саны кіруі мүмкін, бірақ бір ғана ток көзі кіре алады, себебі тізбекте сыртқы элементтерге тәуелді емес әрбір қорек көзінің қасиеті қарсы келеді.
Слайд 41 - суреттегі а және в нүктелерінің арасында кернеудің келуі
Бұл айырмада кез келген потенциал санын қалауынша қарама қарсы қосып, содан кейін қос-қостан біріктіруге болады. (Мысалы: потенциалды нүктесінде элементтерінің жалғауы)
Осылайша, кез келген тізбектей жалғануды бір эквивалентті резисторы және бір ЭҚК бар тізбектей түрлендіруге болады. Эквивалентті резистордың кедергісі жалғануына кіретін барлық кедергілердің қосындысына тең, ал эквивалентті ЭҚК көзі жалғануға кіретін ЭҚК көзінің алгебралық қосындысына тең.
Слайд 5Тізбектей жалғанған элементтер коммутативті қасиетке ие, яғни жалғануының кез келген элементтері
R эквивалентті кедергісі оң қосылыстардың қосындысын білдіретіндіктен ,
R > rmax,мұндағы rmax – жалғануға кіретін кедергілердің ең үлкені.
Егер тізбектей жалғану электр тізбегінің түйініне қосылса, онда оның анықтамасы тармақтың анықтамасына ұқсас. Бұл тармақ тек тізбектей жалғану арқылы құрылуы мүмкін деген сөз.
Слайд 61-есеп
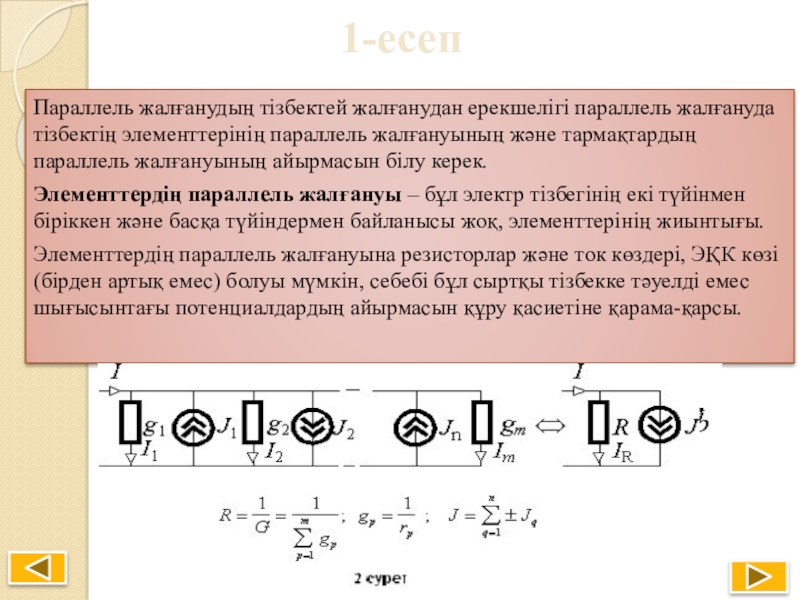
Параллель жалғанудың тізбектей жалғанудан ерекшелігі параллель жалғануда тізбектің элементтерінің параллель
Элементтердің параллель жалғануы – бұл электр тізбегінің екі түйінмен біріккен және басқа түйіндермен байланысы жоқ, элементтерінің жиынтығы.
Элементтердің параллель жалғануына резисторлар және ток көздері, ЭҚК көзі (бірден артық емес) болуы мүмкін, себебі бұл сыртқы тізбекке тәуелді емес шығысынтағы потенциалдардың айырмасын құру қасиетіне қарама-қарсы.
Слайд 7Параллель жалғанудың барлық элементтері екі түйінге байланысқан және осы түйіндердің арасындағы
Параллель жалғануда өтетін I = I1+I2+...+In -J1+J2+...+Jm. жалпы токты элементтердегі токтардың қосындысы ретінде көрсетуге болады.
Осыдан ,токтардың орнына кернеумен кедергіні қолдана отырып келесі теңдеуді аламыз
Слайд 8Қорыта келгенде, әр түрлі саны бар элементтердің параллель жалғануын бір эквивалентті
Тізбектей жалғануға ұқсас, (2) ережесінен шығатын паралель жалғану да коммутативтілік қасиетіне ие.
Слайд 9Параллель жалғану кезінде бөлек элементтердің өткізгіштіктерінің қосындысы болатын G эквивалентті өткізгіштігіне
Слайд 112 - есеп
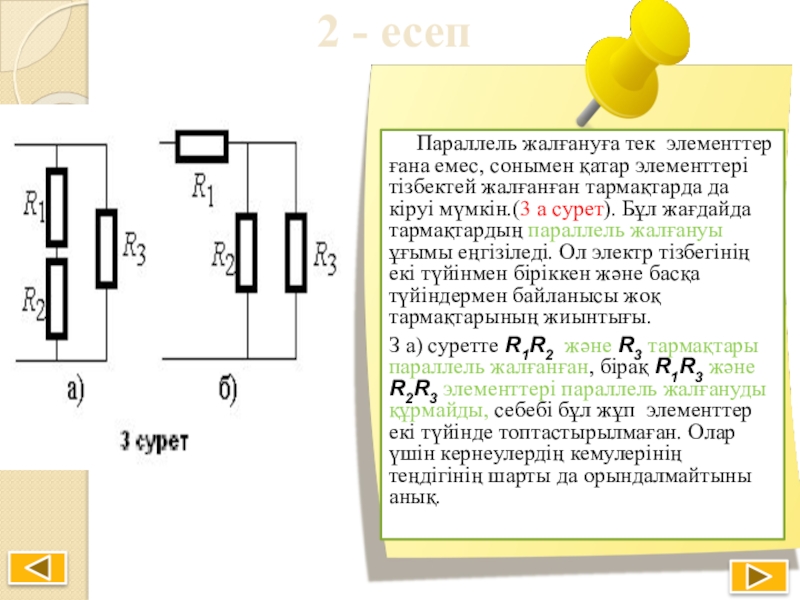
Параллель жалғануға тек элементтер ғана емес,
З а) суретте R1R2 және R3 тармақтары параллель жалғанған, бірақ R1R3 және R2R3 элементтерi параллель жалғануды құрмайды, себебі бұл жұп элементтер екi түйiнде топтастырылмаған. Олар үшiн кернеулердiң кемулерiнiң теңдiгiнiң шарты да орындалмайтыны анық.
Слайд 12 3-есеп
3-шi суреттегі сұлба аралас қосылысқа жатады, яғни элементтер мен тізбек
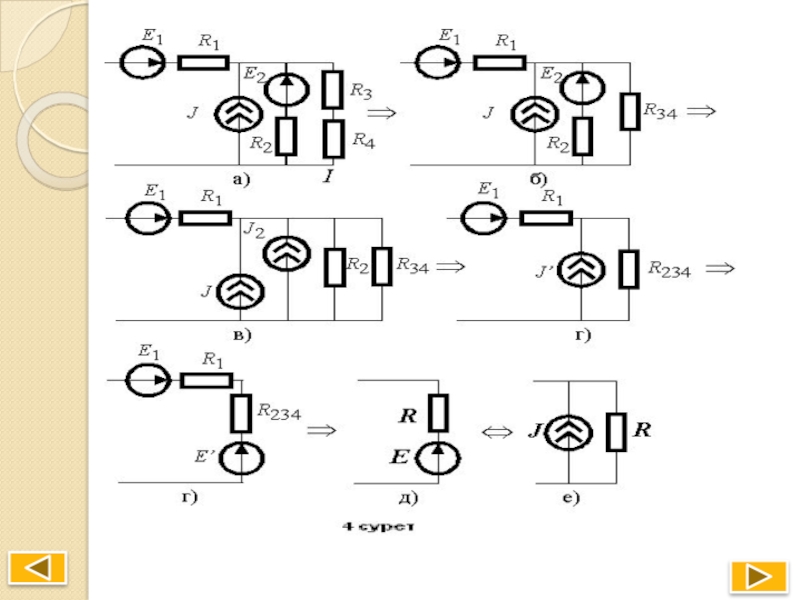
Кез келген электр тізбегін элементтерінің жалғануларына кезеңді өзгертулер еңгізу арқылы R-E тізбектей немесе G-J паралель жалғануына түрлендіруге болады. Бұл әдіс күрделі есептер шығаруға мүмкіндік береді, әсіресе, тізбектің тармағының тәртібін анықтауда нәтижелі. 4-суретте осындай өзгертулерге мысал көрсетілген.
Түрлендірудің жеке кезеңдерінде элементтердің параметрлері келесі ережелерден шығады: R34=R3+R4 ;J2=E2/R2 ; R234=(R2R34)/(R2+R34) ; J' =J+J2 ; E' = J'R234 ; R = R1+R234 ; E = E' - E1 ; J=E/R.
Слайд 14Тізбектегі ажырау нүктелеріне қатысты кедергіні (кірістегі кедергі) анықтау - тізбекті түрлендірумен
Слайд 15Бұл әдістің негізі – эквивалентті түрлендірудің алдында тізбектегі барлық ЭКҚ және
Алдымен барлық көздерді олардың эквивалентті кедергісімен алмастырып, суретте ажырауды a және b анық нүктелерімен көрсетейік (5б сурет). Енді мәселе анық көрінеді, себебі тізбек а нүктесінен b нүктесіне дейін R1 және R3 кедергілері тізбектей жалғанған
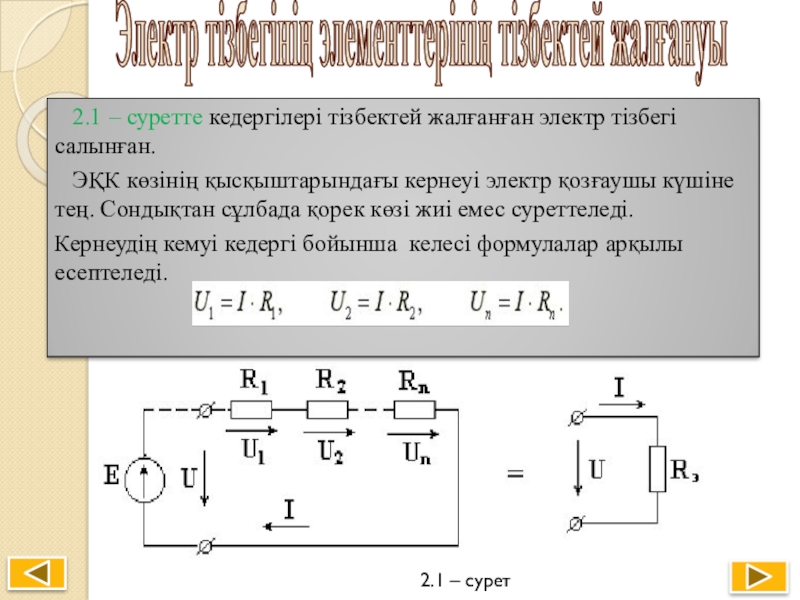
Слайд 16 2.1 – суретте кедергілері тізбектей жалғанған электр тізбегі салынған.
Кернеудің кемуі кедергі бойынша келесі формулалар арқылы есептеледі.
2.1 – сурет
Электр тізбегінің элементтерінің тізбектей жалғануы
Слайд 17Кихгофтың екінші заңына сәйкес электр тізбегінің кірісіндегі кернеуі тізбектегі кедергінің кернеудің
мұндағы - эквивалентті кедергі.
Электр тізбегінің эквивалетті кедергісі n тізбектей қосылған элементтерден құрылған элементттерінің кедергілернің қосындысына тең.
Слайд 182.2 суреттегі электр тізбектегі кедергілердің параллель жалғануы көрсетілген.
Параллель тармақтағы токтар келесі
Мұндағы - 1-ші, 2-ші және n-ші тармақтардың өткізгіштіктері.
Электр тізбегіндегі элементтердің параллель жалғануы
Слайд 19Кирхгофтың бірінші заңына сәйкес, сызбадағы тармақталмаған бөліктегі ток параллель қосылған токтардың
Мұндағы,
Параллель қосылған n элементтен тұратын электр тізбегінің эквивалентті өткізгіштігі параллель қосылған элементтер өткізгіштіктерінің қосындысына тең.
Тізбектің эквивалентті кедергісі деп эквивалентті өткiзгiштіктің керi шамасына тең
Слайд 20Электр сызбасында 3 параллель қосылған кедергілер болсын, онда эквивалентті өткізгіш
Бірдей n
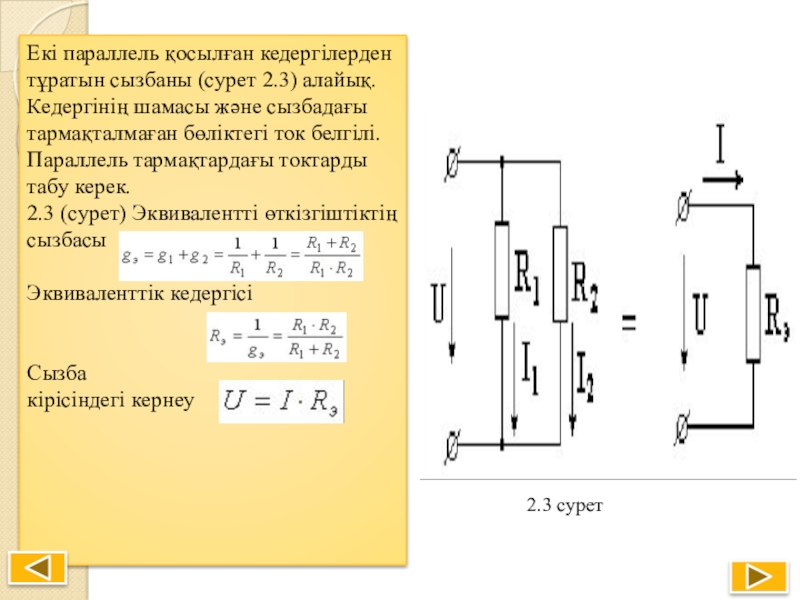
Слайд 21Екі параллель қосылған кедергілерден тұратын сызбаны (сурет 2.3) алайық. Кедергінің шамасы
табу керек.
2.3 (сурет) Эквивалентті өткізгіштіктің сызбасы
Эквиваленттік кедергісі
Сызба
кірісіндегі кернеу
2.3 сурет
Слайд 22Параллель тармақтарындағы токтар
Осыған ұқсас
Параллель тармактағы ток сұлбаның тармақталмаған
Слайд 23Үшбұрыштың эквивалентті кедергісі арқылы жұлдызшаның құрылуы.
Кей сұлбада тізбектей және параллель жалғанған
Слайд 24Эквивалентті кедергілер жұлдызы сәулесіннің кедергісі үшбұрыштың іргелес жақтарының кедерглерінің көбейтіндісін үшбұрыштың
Көрсетілген ережелерге сәйкес, жұлдыздың сәулелер кедергісі келесі формулаллармен анықталады.
Алынған сұлбаның эквивалентті кедергісі төмендегі формулармен анықталады
R0 и Rλ1 кедергілері тізбектей жалғанған , Rλ1 + R4 и Rλ3 + R5 кедергілері бар тармақтар параллель жалғанған
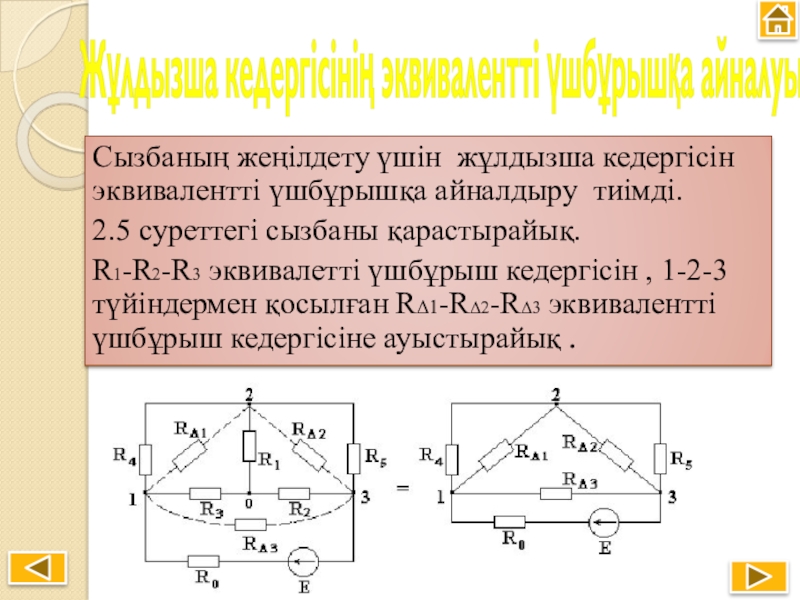
Слайд 25Жұлдызша кедергісінің эквивалентті үшбұрышқа айналуы
Сызбаның жеңілдету үшін жұлдызша кедергісін эквивалентті үшбұрышқа
2.5 суреттегі сызбаны қарастырайық.
R1-R2-R3 эквивалетті үшбұрыш кедергісін , 1-2-3 түйіндермен қосылған RΔ1-RΔ2-RΔ3 эквивалентті үшбұрыш кедергісіне ауыстырайық .
Слайд 26Кедергiлер жұлдызының эквивалентті үшбұрышқа өзгертуi
Эквивалентті үшбұрыш кедергілерінің жақтарының кедергісі жұлдыздың екі
Өзгертiлген сұлбаның эквивалентті кедергiсі тең: