Учебные цели занятия
В результате проведенного лекционного занятия курсант должен:
знать:
- основные понятия, современные теории, законы,
уметь:
- использовать основные понятия, законы для решения задач сопротивления материалов.
Воспитательные цели
На занятии необходимо формировать и развивать у курсантов:
- любовь к Отечеству, гордость и ответственность за принадлежность к Вооруженным Силам Российской Федерации и их офицерскому корпусу;
- офицерскую честь и достоинство, дисциплинированность;
-общую культуру, стремление к самосовершенствованию.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Анализ напряженного и деформированного состояния в точке тела. Сложное сопротивление, расчет по теориям прочности
Содержание
- 1. Анализ напряженного и деформированного состояния в точке тела. Сложное сопротивление, расчет по теориям прочности
- 2. Тема 19. Анализ напряженного и деформированного состояния
- 3. Определить напряженно-деформируемое состояние какого-либо тела под влиянием
- 4. Расположим все напряжения, определяющие собой напряжённое состояние
- 5. Эту симметричную табличку (матрицу) называют Таким образом,
- 6. 19.2. Понятие о теории прочностиОпределение коэффициента запаса
- 7. При сложном напряженном состоянии прежде всего устанавливают
- 8. 19.3. Наибольшие напряжения в балке с постоянным сечением при сложном изгибеРассмотрим пример косого изгиба.
- 9. Таким образом, случай косого изгиба можно всегда
- 10. 19.4. Положение нейтральной линии в сечении балки
- 11. Определив из последнего выражения отношение у/z, найдем
- 12. Положение нейтральной линии в сечении балки при внецентренном растяженииВозьмем общий случай внецентренного растяжения(сжатия).
- 13. В любой точке поперечного сечения нормальное напряжение
- 14. 19.5. Проверка прочности балки при сложном изгибе
- 15. Задание на самостоятельную работу1. Кичин И.Н. Сопротивление
Слайд 1Тема 19. Анализ напряженного и деформированного состояния в точке тела. Сложное
Слайд 2Тема 19. Анализ напряженного и деформированного состояния в точке тела. Сложное
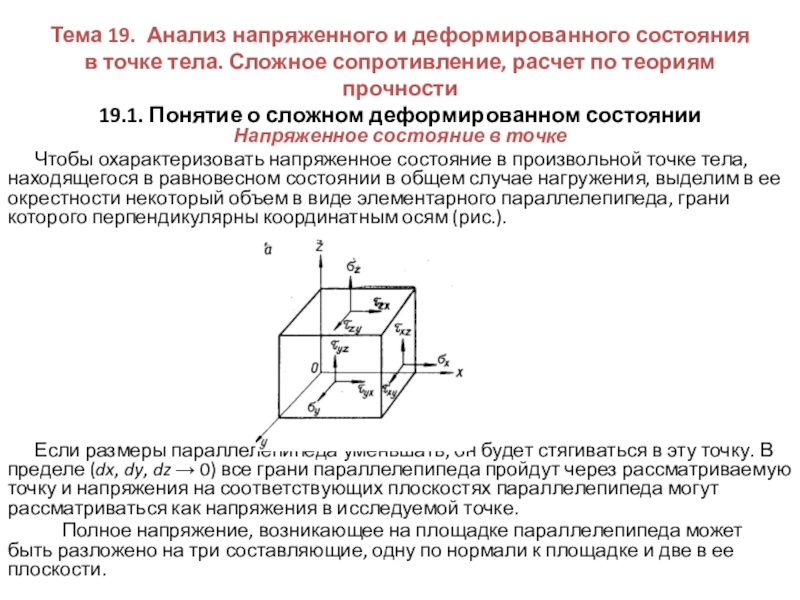
Напряженное состояние в точке
Чтобы охарактеризовать напряженное состояние в произвольной точке тела, находящегося в равновесном состоянии в общем случае нагружения, выделим в ее окрестности некоторый объем в виде элементарного параллелепипеда, грани которого перпендикулярны координатным осям (рис.).
Если размеры параллелепипеда уменьшать, он будет стягиваться в эту точку. В пределе (dx, dy, dz → 0) все грани параллелепипеда пройдут через рассматриваемую точку и напряжения на соответствующих плоскостях параллелепипеда могут рассматриваться как напряжения в исследуемой точке.
Полное напряжение, возникающее на площадке параллелепипеда может быть разложено на три составляющие, одну по нормали к площадке и две в ее плоскости.
Слайд 3Определить напряженно-деформируемое состояние какого-либо тела под влиянием приложенных внешних сил —
Напряженное состояние по любой элементарной площадке может быть однозначно охарактеризовано тремя составляющими напряжений.
Вместе с тем три взаимоперпендикулярные площадки характеризуют элементарный объем. В соответствии с этим напряженное состояние элементарного объема может быть определено девятью компонентами напряжений - тремя нормальными и шестью касательными составляющими напряжений.
Слайд 4Расположим все напряжения, определяющие собой напряжённое состояние в рассматриваемой точке, в
Здесь в первой строке расположены все компоненты, имеющие направление, параллельное оси Х, соответственно во второй строке - все компоненты, имеющие направление, параллельное оси У, в третьей - все компоненты, имеющие направление, параллельное оси Z.
Кроме того, в первом столбце сгруппировались напряжения, действующие на площадке, нормаль к которой параллельна оси Х, во втором столбце - все напряжения на площадке с нормалью, параллельной оси У, в третьем столбце - на площадке с нормалью, параллельной оси Z.
Слайд 5Эту симметричную табличку (матрицу) называют Таким образом, можно констатировать, что напряжённое
состояние в заданной точке в данный момент вполне определено, если задан тензор напряжений для этой точки и для того же момента времени.
У данной матрицы имеются некоторые замечательные свойства, рассмотрение которых расширяет наши представления о напряжённом состоянии в точке. В частности, через каждую пространственно напряжённую точку можно провести несколько замечательных плоскостей, на которых действующие напряжения являются характерными.
Так существуют три взаимно перпендикулярные площадки, по которым касательные напряжения равны нулю, а действующие на них нормальные напряжения имеют характерные для данной точки значения - максимум, минимум и минимакс.
Это есть главные площадки для нормальных напряжений. Значения напряжений на этих площадках называются главными нормальными напряжениями.
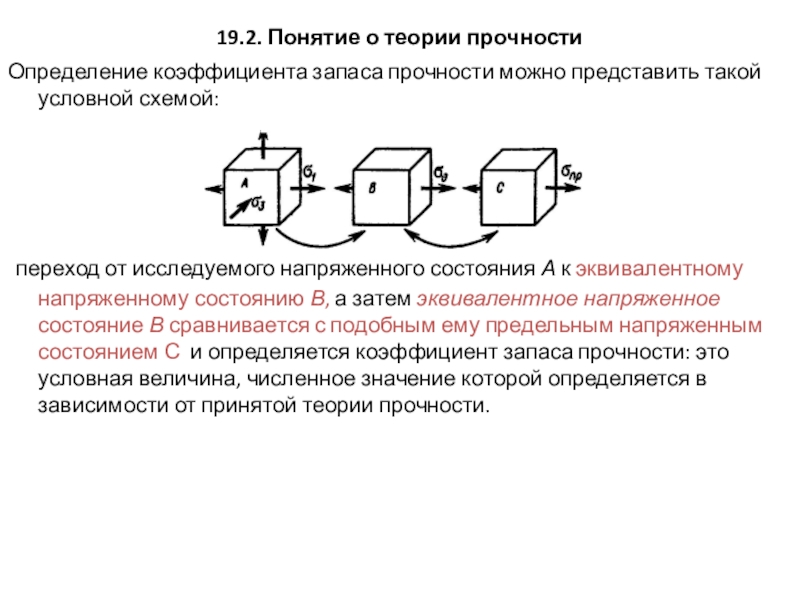
Слайд 619.2. Понятие о теории прочности
Определение коэффициента запаса прочности можно представить такой
переход от исследуемого напряженного состояния А к эквивалентному напряженному состоянию В, а затем эквивалентное напряженное состояние В сравнивается с подобным ему предельным напряженным состоянием С и определяется коэффициент запаса прочности: это условная величина, численное значение которой определяется в зависимости от принятой теории прочности.
Слайд 7При сложном напряженном состоянии прежде всего устанавливают причину разрушения материала, используя
Первая гипотеза прочности была выдвинута Галилеем в XVII в. и состояла в том, что причиной разрушения материала является наибольшее нормальное напряжение растяжения или сжатия σ без учета двух других главных напряжений.
Вторая гипотеза была выдвинута в 1682 г. Э. Мариоттом; согласно этой гипотезе, прочность материала в исследуемой точке достигает критического состояния при максимальном значении линейной деформации εмах.
Третья гипотеза, предложенная Ш. Кулоном в 1773 г., предполагает, что предельное напряженное состояние возникает в момент, когда в двух взаимно перпендикулярных сечениях, проведенных через исследуемую точку, наибольшие касательные напряжения достигают предельного значения, при котором возможно разрушение путем сдвига и скольжения одной части материала по другой.
Четвертая гипотеза, предложенная О. Мором в 1900 г., базируется не на каком-либо одном факторе σ, εмах или τ, а на двух σ и τ, а потому она более совершенна, чем предыдущие три
Пятая гипотеза прочности иначе называется гипотезой энергии формоизменения, и критерий перехода от исследуемого напряженного состояния А к эквивалентному состоянию В основан на том, что предельное напряженное состояние возникает при некотором значении потенциальной энергии, накапливаемой элементом конструкции при изменении только его формы.
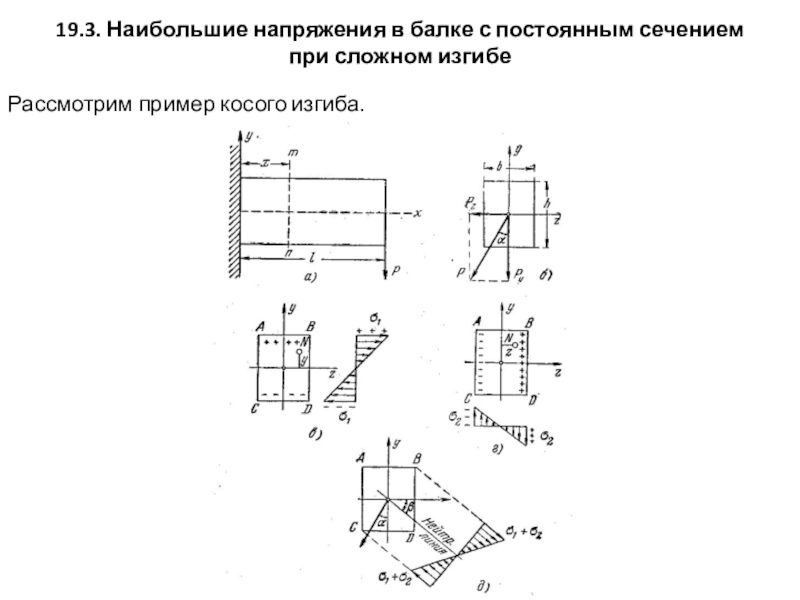
Слайд 819.3. Наибольшие напряжения в балке с постоянным сечением при сложном изгибе
Рассмотрим
Слайд 9Таким образом, случай косого изгиба можно всегда свести к двум плоским
при одновременном действии двух моментов напряжение в любой точке сечения равно алгебраической сумме напряжений σ1 и σ2, тогда
Слайд 1019.4. Положение нейтральной линии в сечении балки Положение нейтральной линии в
Слайд 11Определив из последнего выражения отношение у/z, найдем тангенс угла (β),составляемого нейтральной
из формулы видно, что для таких сечений, у которых Jz=Jy (квадрат, круг) нейтральная линия всегда будет перпендикулярна к плоскости действия изгибающего момента, в котором и будет происходить деформация изгиба, т.е. в балках, у которых все центральные оси поперечных сечений (правильные фигуры) являются главными, не может быть косого изгиба.
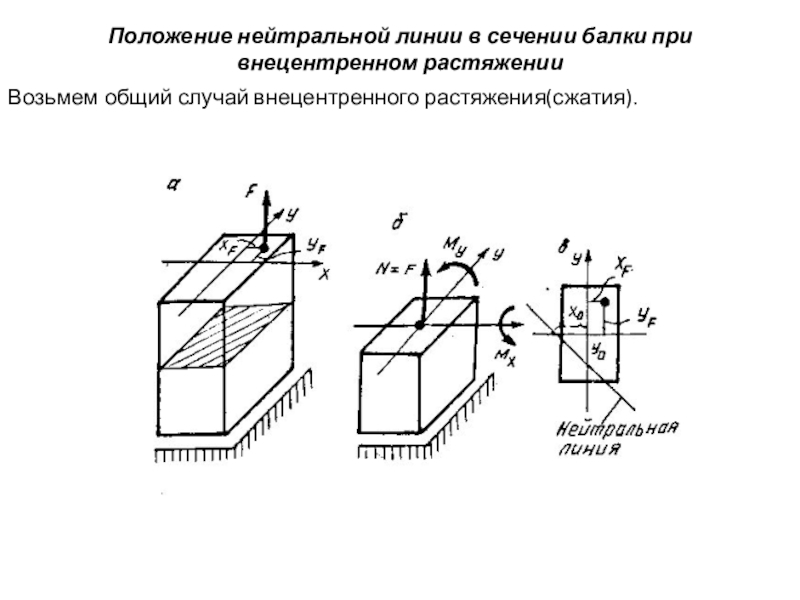
Слайд 12Положение нейтральной линии в сечении балки при внецентренном растяжении
Возьмем общий случай
Слайд 13В любой точке поперечного сечения нормальное напряжение определится формулой
нахождения нейтральной линии
эта линия не проходит через центр тяжести сечения, ее положение определяется точками пересечения с осями координат:
Слайд 15Задание на самостоятельную работу
1. Кичин И.Н. Сопротивление мтериалов. Учебное пособие.- Ейск,
2. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. Учебное пособие. – М. :Высшая школа, 2003. - (с. 326-337).
Дополнительная литература
1. Феодосьев .В.И. Сопротивление материалов. Учебник для втузов.- М.: Наука, 1986. - (с. 252-279).