- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Аксиома параллельных прямых
Содержание
- 1. Аксиома параллельных прямых
- 2. Домашнее задание.п.27-28, приложение1,вопросы 7-11.№199, №211а,бЛогинова Н.В. МБОУ «СОШ №16»
- 3. Закончи предложение.1. Прямая х называется секущей
- 4. Проверка1)…если она пересекает их в двух точках2)…83)…секущей4)…накрест лежащими5)…односторонними6)…равныЛогинова Н.В. МБОУ «СОШ №16»
- 5. Найдите соответствие1) a | | b, так
- 6. Теорема Теорема
- 7. Мы использовали и другие аксиомы , хотя
- 8. Сравнение 2-х углов основано на аналогичной аксиоме:От
- 9. Сначала формулируются исходные положения - аксиомыНа их
- 10. МавсДокажем, что через точку М можно провести
- 11. Аксиома параллельных прямыхЧерез точку, не лежащую на
- 12. 1. Если прямая пересекает одну
- 13. Решение задач
- 14. Отметить знаком «+» правильные утверждения и знаком
- 15. Вариант 11. «-»2. «-»3. «-»4. «+»5. «+»Вариант
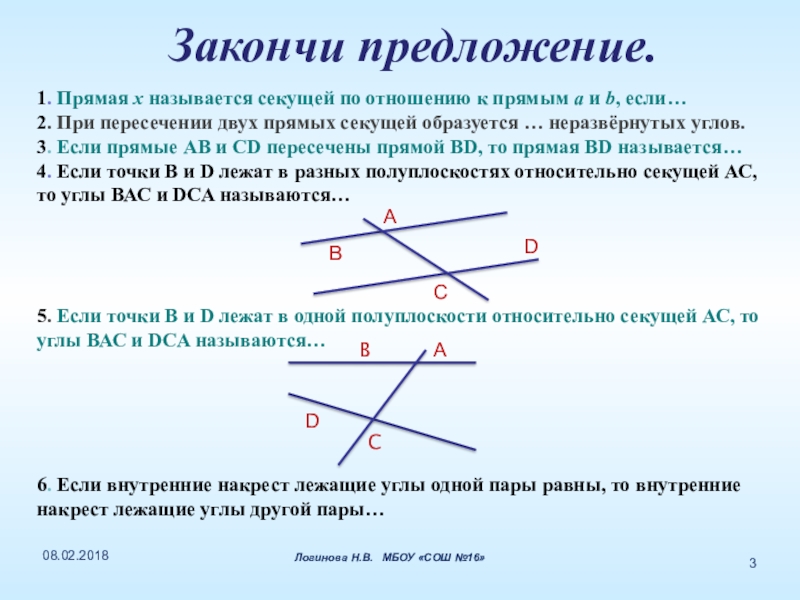
Слайд 3 Закончи предложение.
1. Прямая х называется секущей по отношению к прямым
2. При пересечении двух прямых секущей образуется … неразвёрнутых углов.
3. Если прямые АВ и СD пересечены прямой ВD, то прямая ВD называется…
4. Если точки В и D лежат в разных полуплоскостях относительно секущей АС,
то углы ВАС и DCA называются…
5. Если точки В и D лежат в одной полуплоскости относительно секущей АС, то
углы ВАС и DCA называются…
6. Если внутренние накрест лежащие углы одной пары равны, то внутренние
накрест лежащие углы другой пары…
А
В
С
D
А
B
C
D
Логинова Н.В. МБОУ «СОШ №16»
Слайд 4Проверка
1)…если она пересекает их в двух точках
2)…8
3)…секущей
4)…накрест лежащими
5)…односторонними
6)…равны
Логинова Н.В. МБОУ
Слайд 5Найдите соответствие
1) a | | b, так как
2) a | | b, так как
соответственные
углы равны
3) a | | b, так как
сумма внутренних
односторонних
углов равна 180°
m
a
b
1500
300
a)
a
b
m
450
450
b)
a
b
m
1500
1500
c)
Логинова Н.В. МБОУ «СОШ №16»
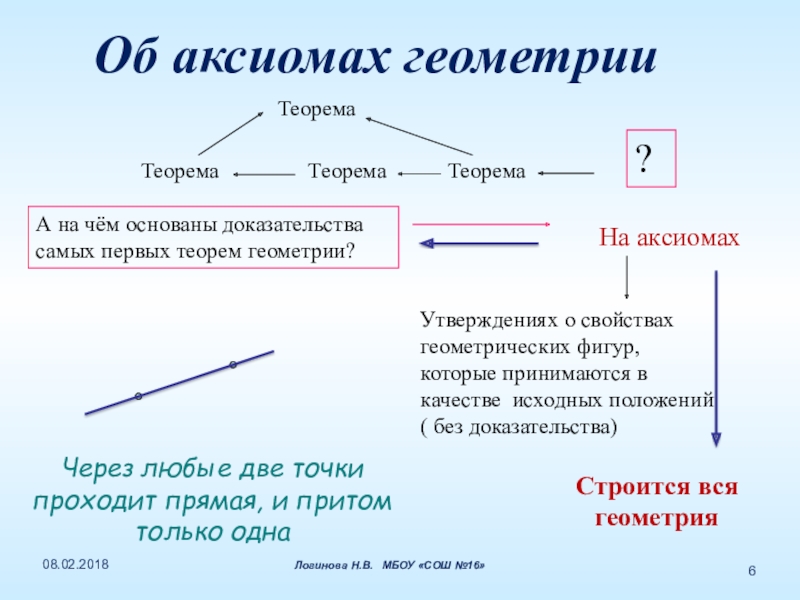
Слайд 6Теорема
Теорема
А на чём основаны доказательства самых первых теорем геометрии?
На аксиомах
Утверждениях о свойствах геометрических фигур, которые принимаются в качестве исходных положений ( без доказательства)
?
Об аксиомах геометрии
Строится вся геометрия
Через любые две точки
проходит прямая, и притом
только одна
Логинова Н.В. МБОУ «СОШ №16»
Слайд 7Мы использовали и другие аксиомы , хотя особо не выделяли их.
Так,
Логинова Н.В. МБОУ «СОШ №16»
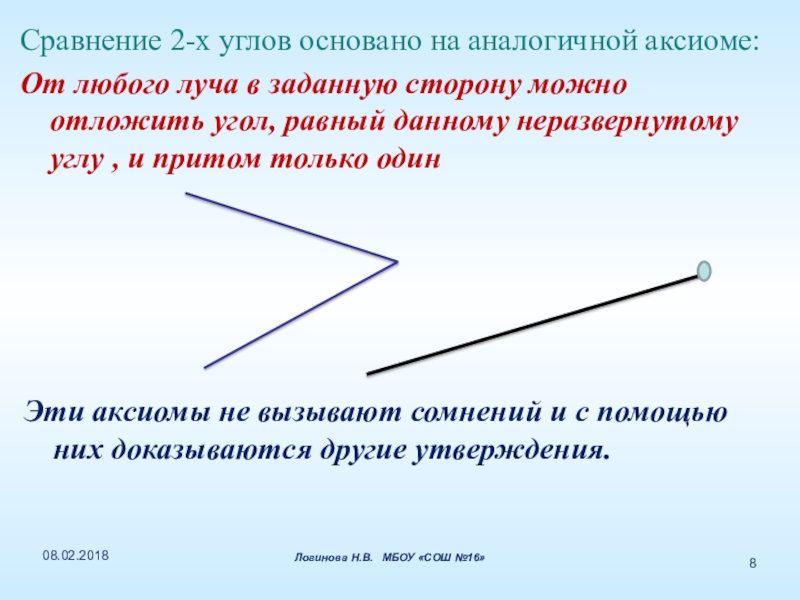
Слайд 8Сравнение 2-х углов основано на аналогичной аксиоме:
От любого луча в заданную
Эти аксиомы не вызывают сомнений и с помощью них доказываются другие утверждения.
Логинова Н.В. МБОУ «СОШ №16»
Слайд 9Сначала формулируются исходные положения - аксиомы
На их основе, путём логических рассуждений
Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
Логинова Н.В. МБОУ «СОШ №16»
Слайд 10М
а
в
с
Докажем, что через точку М можно провести прямую, параллельную прямой а.
а ┴ с =>а в
в ┴ с
Можно ли через т.М провести еще одну прямую , параллельную прямой а ?
в1
Через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.
Можно ли это утверждение доказать?
Ответ на этот непростой вопрос дал великий русский математик
Аксиома параллельных прямых
Николай Иванович Лобачевский
1792-1856
Слайд 11Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит только
Аксио́ма – исходное утверждение, принимаемое истинным без доказательств, и которое в последующем служит «фундаментом» для построения какой-либо теории, дисциплины.
Теоре́ма – утверждение, для которого в рассматриваемой теории существует доказательство.
Следствие – утверждение, которое выводится из теорем и аксиом.
Логинова Н.В. МБОУ «СОШ №16»
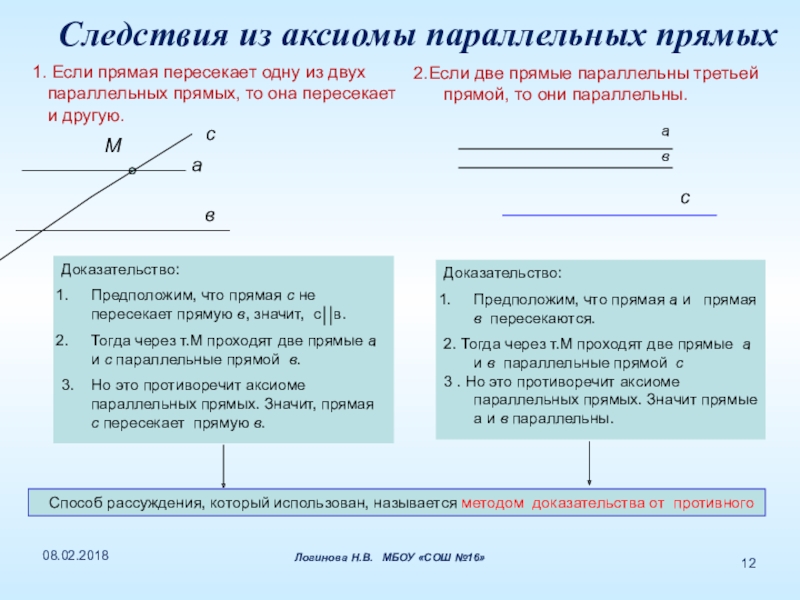
Слайд 12 1. Если прямая пересекает одну из двух параллельных прямых,
2.Если две прямые параллельны третьей прямой, то они параллельны.
а
в
М
с
Доказательство:
Предположим, что прямая с не пересекает прямую в, значит, с в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых. Значит, прямая с пересекает прямую в.
а
в
с
Доказательство:
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых. Значит прямые а и в параллельны.
Способ рассуждения, который использован, называется методом доказательства от противного
Следствия из аксиомы параллельных прямых
Логинова Н.В. МБОУ «СОШ №16»
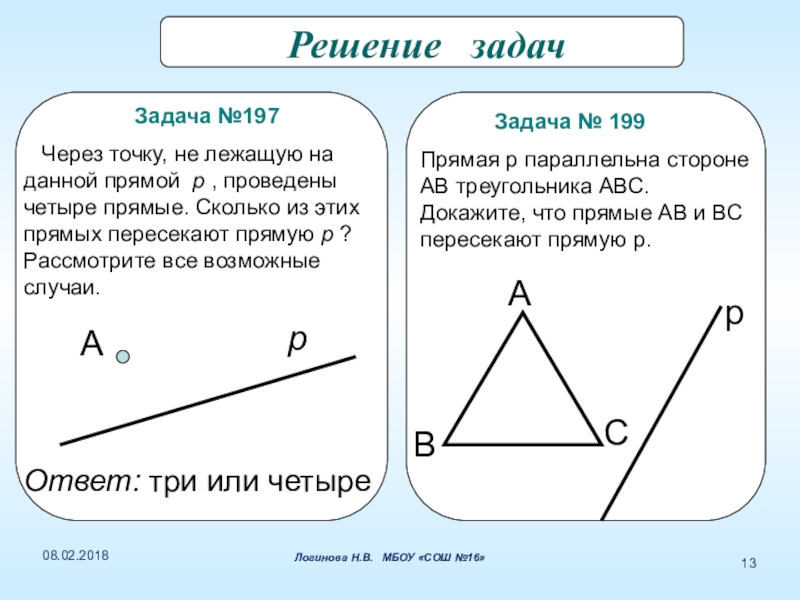
Слайд 13 Решение задач
Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи.
А
р
Задача № 199
Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АВ и ВС пересекают прямую р.
А
В
С
р
Ответ: три или четыре
Логинова Н.В. МБОУ «СОШ №16»
Слайд 14Отметить знаком «+» правильные утверждения и знаком «-» - ошибочные.
Вариант 1
1.
2. Через любые две точки проходит прямая.
3. На любом луче от начала можно отложить отрезки, равные данному, причем сколько угодно много.
4.Через точку не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
5. Если две прямые параллельны третьей, то они параллельны между собой.
Вариант 2
1. Аксиомой называется математическое утверждение о свойствах геометрических фигур, принимаемое без доказательства.
2. Через любые две точки проходит прямая, и притом только одна.
3. Через точку, не лежащую на данной прямой, проходят только две прямые, параллельные данной.
4. Если прямая пересекает одну из двух параллельных прямых, то она перпендикулярна другой прямой.
5. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Логинова Н.В. МБОУ «СОШ №16»
Слайд 15Вариант 1
1. «-»
2. «-»
3. «-»
4. «+»
5. «+»
Вариант 2
1. «+»
2. «+»
3. «-»
4.
5. «+»
Логинова Н.В. МБОУ «СОШ №16»
«Геометрия полна приключений,
потому что за каждой задачей скрывается приключение мысли.
Решить задачу – это значит пережить приключение».
(В. Произволов)