- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Сопряжения
Содержание
- 1. Сопряжения
- 2. Сопряжение –это плавный переход одной линии в
- 3. Сопряжение острого или тупого угла.Для построения сопряжения
- 4. Сопряжение двух параллельных прямых.Пусть заданы две параллельные
- 5. Сопряжение дуг двух окружностей дугой заданного радиуса.Внешнее
- 6. Внутреннее сопряжение дуг окружностей дугой заданного радиуса.Даны
- 7. Вывод:Определяя величину радиусов вспомогательных дуг следует:а) при
- 8. Эллипс.Эллипс – это плоская кривая, являющаяся
- 9. Построение эллипса.Для построения эллипса проведем взаимно перпендикулярные
- 10. Выполнить чертеж по наглядному изображению детали.
Слайд 1У.№5.
Сопряжения. Построение эллипса.
Понятие сопряжения. Построение сопряжения прямого угла, сопряжение острого и
Сопряжение двух параллельных прямых. Сопряжение окружностей. Построение эллипса.
Слайд 2Сопряжение –это плавный переход одной линии в другую. Общая для сопрягаемых
Сопряжение прямого угла радиусом сопряжения (R) .
Для нахождения точек сопряжения поставим ножку циркуля в вершину угла и сделаем засечки на его сторонах на расстоянии R от вершины.
Полученные точки (a и b) являются точками сопряжения.
Раствором циркуля радиуса R из т.(a) и т.(b) проведем дуги внутри угла.
Полученная точка (О)- центр сопряжения.
Из т. О описываем дугу заданного радиуса от т.(а) до т. (b).
Обводим сначала дугу, а потом прямые линии.
А В
а О
R
b
R= AB
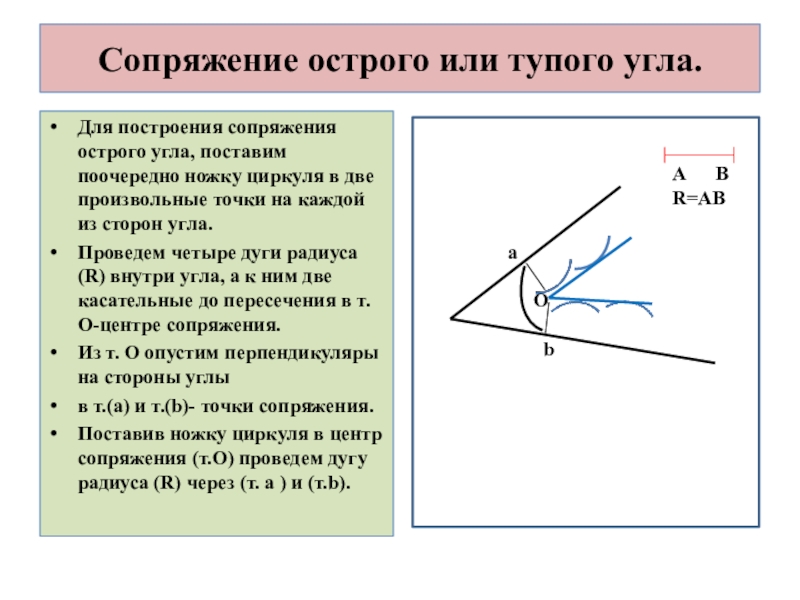
Слайд 3Сопряжение острого или тупого угла.
Для построения сопряжения острого угла, поставим поочередно
Проведем четыре дуги радиуса (R) внутри угла, а к ним две касательные до пересечения в т. О-центре сопряжения.
Из т. О опустим перпендикуляры на стороны углы
в т.(а) и т.(b)- точки сопряжения.
Поставив ножку циркуля в центр сопряжения (т.О) проведем дугу радиуса (R) через (т. a ) и (т.b).
A B
R=AB
a
O
b
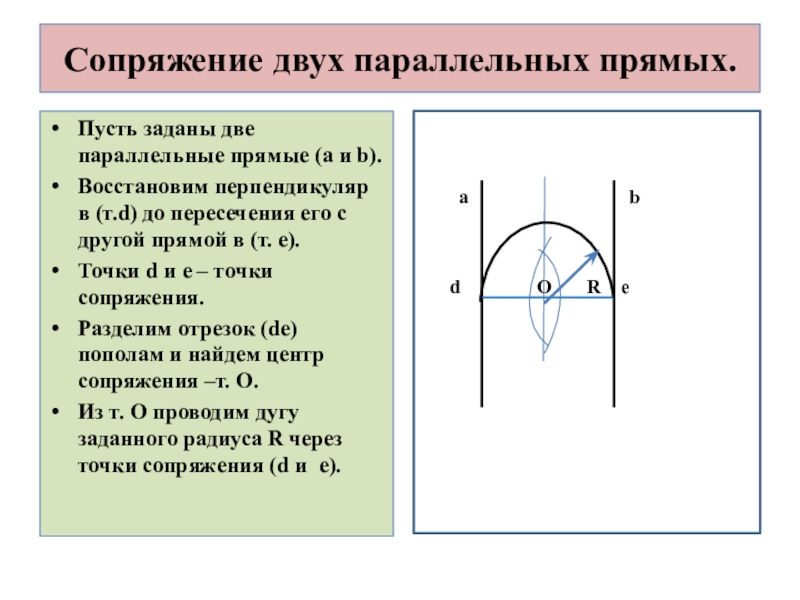
Слайд 4Сопряжение двух параллельных прямых.
Пусть заданы две параллельные прямые (а и b).
Восстановим
Точки d и e – точки сопряжения.
Разделим отрезок (de) пополам и найдем центр сопряжения –т. О.
Из т. О проводим дугу заданного радиуса R через точки сопряжения (d и e).
d O R e
a b
Слайд 5Сопряжение дуг двух окружностей дугой заданного радиуса.
Внешнее сопряжение дуг двух окружностей:
Даны
( R1 и R2).
Построим сопряжение дугой радиуса (R);
Для нахождения центра сопряжения проводим две вспомогательные дуги радиусами ( R1+R ) и (R2+R);
Точка их пересечения Т.О- центр сопряжения.
Проводим дугу радиуса R из т.О, соединяя точки сопряжения.
О
R+R1
R+R2
R
R1
R2
R
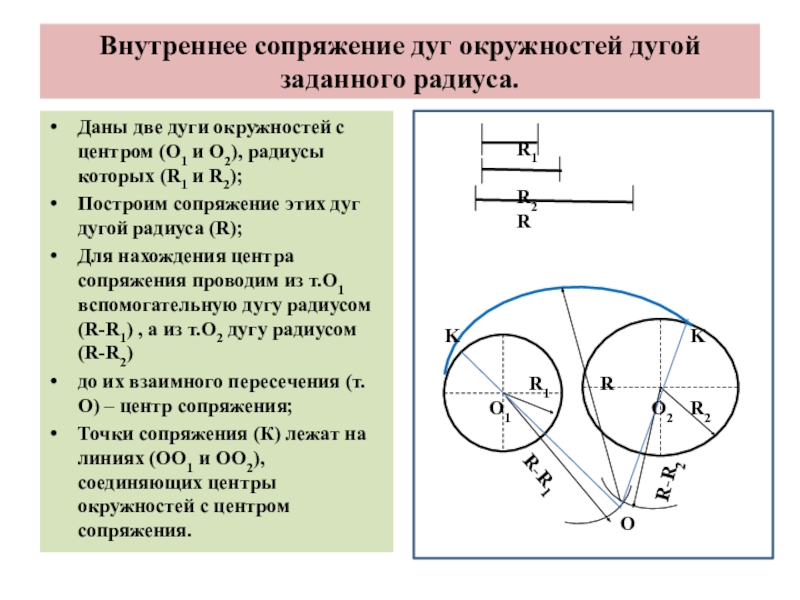
Слайд 6Внутреннее сопряжение дуг окружностей дугой заданного радиуса.
Даны две дуги окружностей с
Построим сопряжение этих дуг дугой радиуса (R);
Для нахождения центра сопряжения проводим из т.О1 вспомогательную дугу радиусом (R-R1) , а из т.О2 дугу радиусом (R-R2)
до их взаимного пересечения (т.О) – центр сопряжения;
Точки сопряжения (К) лежат на линиях (ОО1 и ОО2), соединяющих центры окружностей с центром сопряжения.
R1
R2
R
K K
R1 R
O1 O2 R2
R-R1
R-R2
O
Слайд 7Вывод:
Определяя величину радиусов вспомогательных дуг следует:
а) при внешнем сопряжении брать сумму
т.е. (R1 +R); (R2 +R); (учебник, рис.69)
б) при внутреннем сопряжении нужно использовать разность радиуса сопряжения и радиусов заданных дуг окружностей,
т.е. (R-R1 ); (R-R2 ). Учебник, рис 70.
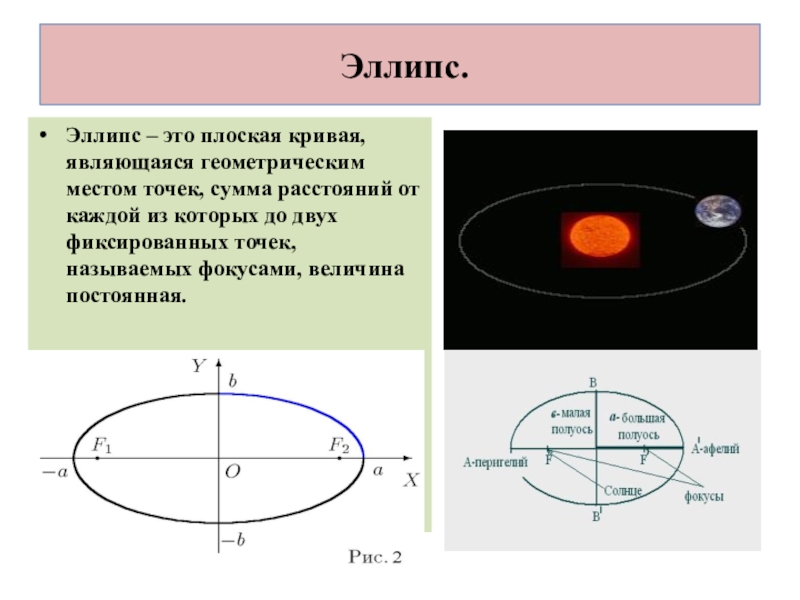
Слайд 8 Эллипс.
Эллипс – это плоская кривая, являющаяся геометрическим местом точек, сумма
Слайд 9Построение эллипса.
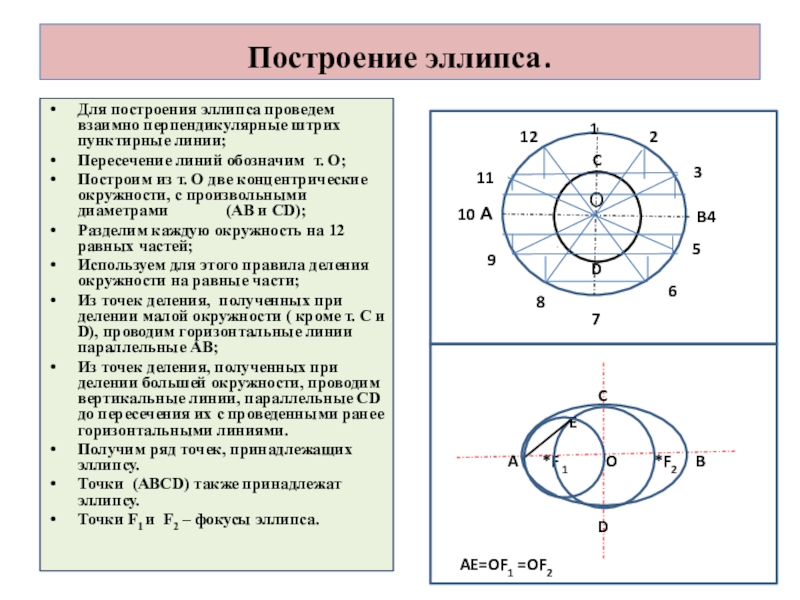
Для построения эллипса проведем взаимно перпендикулярные штрих пунктирные линии;
Пересечение линий
Построим из т. О две концентрические окружности, с произвольными диаметрами (АВ и CD);
Разделим каждую окружность на 12 равных частей;
Используем для этого правила деления окружности на равные части;
Из точек деления, полученных при делении малой окружности ( кроме т. С и D), проводим горизонтальные линии параллельные АВ;
Из точек деления, полученных при делении большей окружности, проводим вертикальные линии, параллельные СD до пересечения их с проведенными ранее горизонтальными линиями.
Получим ряд точек, принадлежащих эллипсу.
Точки (ABCD) также принадлежат эллипсу.
Точки F1 и F2 – фокусы эллипса.
1
2
3
B4
6
10 А
О
C
D
7
8
9
11
12
5
A *F 1 O *F2 B
C
D
E
AE=OF1 =OF2
Слайд 10
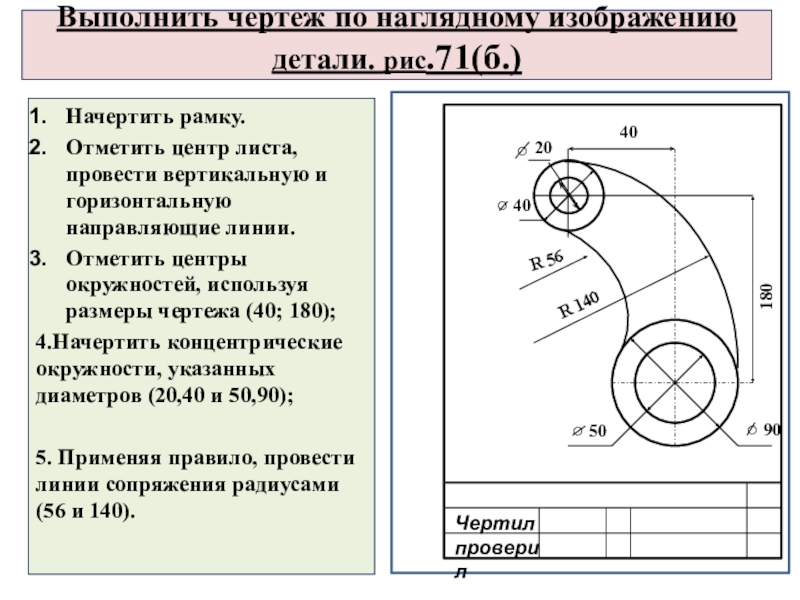
Выполнить чертеж по наглядному изображению детали. рис.71(б.)
Начертить рамку.
Отметить центр листа, провести
Отметить центры окружностей, используя размеры чертежа (40; 180);
4.Начертить концентрические окружности, указанных диаметров (20,40 и 50,90);
5. Применяя правило, провести линии сопряжения радиусами (56 и 140).
40
○
20
○ 40
○ 50
○ 90
R 56
R 140
180
Чертил
проверил