- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Призентация по инженеерной графике по Основам начертательной геометрии
Содержание
- 1. Призентация по инженеерной графике по Основам начертательной геометрии
- 2. Что такое начертательная геометрия?Это что-то техническое, -
- 3. Но продолжая мысль Гюго,
- 4. Все это требовало коллективного труда сотен и
- 5. Как наука начертательная геометрия существует лишь с
- 6. Основоположником и первым профессором начертательной геометрии в
- 7. Хотелось, чтобы начертательная геометрия стала для Вас
- 8. Принятые наименования и обозначенияОсновные плоскости проекции:Горизонтальная
- 9. Сокращенные обозначения производимых операцийЗнак перпендикулярности
- 10. Правила изображений излагаемые в курсе начертательной геометрии
- 11. Параллельное проецирование, когда проецирующие лучи параллельны между
- 12. О - начало координат.Х - ось абсцисс
- 13. АВА1 Проецирование точки на одну и 2
- 14. 212814307212814307Проекция с числовыми отметкамиВ некоторых случаях применяют
- 15. Слайд 15
Слайд 2Что такое начертательная геометрия?
Это что-то техническое, - ответит любой человек.
Это –
Это – наука, без знания которой невозможно техническое творчество, - уверенно ответит опытный инженер.
Основы этой науки преподают в любом техническом заведении.
Разум человеческий
владеет тремя ключами,
открывающими все:
цифрой, буквой, нотой.
В.Гюго
Введение
Слайд 3 Но продолжая мысль Гюго, геометр не может не
Попробуйте потребовать от рабочего изготовить сравнительно простую деталь по её словесному описанию, мы утонули бы в море слов. Кроме того, слова не решают проблему наглядности, так необходимой конструктору и рабочему. Чертеж выполненный в России будет понятен и японскому и американскому инженеру.
Итак, одно из достоинств языка линий – его лаконичность. Сравните «алфавиты» названных языков: в языке слов (в русском алфавите) – 32 элемента (буквы), в языке чисел – 10 (цифр), в языке звуков – 7 (нот), в графическом – 1 (линия или её частный случай – точка). Второе достоинство языка графики – его наглядность.
Издавна люди научились отображать на плоской поверхности разнообразнейшие объекты окружающего их трехмерного мира – животных и деревья, постройки и самих себя. Эти плоские образы в виде точек и линий условно, с большей или меньшей степенью достоверности в зависимости от мастера художника-графика давали представление о прообразах реального мира.
Информация о третьем измерении восполнялась рядом хитроумных примеров. Пока требовалась лишь наглядность, достаточно было интуиции мастера. Но с развитием техники человек потребовал от изображений новое качество – точность. Необходимостью стало точное соответствие между оригиналом и изображением, между прообразом и его образом, между пространственными объектами и их плоскими моделями. А таких пространственных задач, требовавших точного графического отображения жизнь выдвигала все больше. Решение этих задач становилось необходимым при строительстве зданий, конструировании машин, ведении горных разработок, массовом производстве промышленных товаров.
Слайд 4Все это требовало коллективного труда сотен и тысяч людей, точного графического
Перед ней стояли две основные задачи:
Достоверно (однозначно и точно) отобразить пространственную фигуру на плоскости;
По плоскому изображению пространственных фигур можно было судить об их форме и взаимном положении в пространстве.
А это значит, что мост, который перебрасывала начертательная геометрия с берега, на котором лежала страна Стереометрия, на берег страны Планиметрии, должен иметь двухстороннее движение.
Слайд 5Как наука начертательная геометрия существует лишь с конца 18 в. Её
Книга «Начертательная геометрия» вышла в свет в 1799 г., ознаменовав рождение новой науки, значение которой сейчас трудно переоценить.
Конечно отдавая должное Г.Монжу как создателю начертательной геометрии, мы не должны забывать, что он свел в стройную систему разрозненный и многообразный материал, который уже отчасти существовал до него.
В области теории изображения работали Леонардо да Винчи (1452-1519), Альбрехт Дюрер (1471-1528), Жирар Дезарг (1593-1662), Блез Паскаль (1623-1662).
Древняя Русь богата памятниками графики, в которых мы находим совершенно правильные основы построения проекционных чертежей. Такие изобретатели и инженеры, как И.П.Кулибин, И.И.Ползунов, Федор Борзов и другие, выполняли свои чертежи по правилам прямоугольного проецирования задолго до опубликования «Начертательной геометрии» Г.Монжа.
В России начертательную геометрию как предмет стали преподавать с 1810 г. В Институте инженеров путей сообщения (в настоящее время Ленинградский институт инженеров железнодорожного транспорта имени акад. В.Н.Образцова).
Слайд 6Основоположником и первым профессором начертательной геометрии в России был Яков Александрович
Традиции Я.А.Севастьяновым продолжала целая плеяда русских ученых, среди которых видное место принадлежит профессорам А.Х.Редеру (1809-1872), Н.И.Макарову (1824-1904), В.И.Курдюмову (1853-1904) и многие другие. Особенно плодотворной в области графики была деятельность профессора Валериана Ивановича Курдюмова, им было написано 14 работ, охватывающих все разделы начертательной геометрии.
Весьма успешной в советский период была деятельность Н.А.Рыбина, А.К.Власова, Н.А.Глаголева, А.И.Добрякова, Д.И.Каргина, Н.Ф.Четверухина, М.Я.Громова, В.О.Гордона, С.М.Колотова, Г.А.Владимирского и других ученых в области теории изображений. В настоящее время С.А. Фролов, А.В.Бубенников и другие ученые изображений.
Слайд 7Хотелось, чтобы начертательная геометрия стала для Вас строгой, красивой и понятной
Слайд 8Принятые наименования и обозначения
Основные плоскости проекции:
Горизонтальная
Фронтальная П2 (V)
Профильная П3 (W)
Начало координат О
Оси проекций на чертеже Х, У, Z.
Оси проекций при замене плоскостей проекций Х', У'.
Точки в натуре (расположенные в пространстве) А, В, С, S, …; 1, 2, …
Проекции точек на основных плоскостях проекций:
Горизонтальные А1, В1, a, b, …; 11, 21, …
Фронтальные А2, В2, a', b', …; 12, 22, …
Профильные А3, В3, a'', b'',…; 13, 23, …
Прямые и кривые линии частного положения ( в пространстве и на чертеже):
Горизонтальные G (g, g')
Фронтальные F (f, f‘)
Профильные J (j, j‘)
Плоскость в пространстве и на чертеже P, R, Q, G.
Следы плоскости на чертеже G1, G2, G3.
Точка схода следов плоскостей G1, G2, G3.
Слайд 9Сокращенные обозначения производимых операций
Знак перпендикулярности
Знак параллельности ||
Знак совпадения (тождества) ≡
Знак бесконечности ∞
Знак пересечения двух геометрических тел ×
Знак угла
Знак прямого угла
Знак равенства =
Знак «больше» >
Знак «меньше» <
Знак треугольника Δ
Знак принадлежности Є
Слайд 10Правила изображений излагаемые в курсе начертательной геометрии основаны на методах проекции.
Какое слово чаще всего встречается в книгах по начертательной геометрии? Слово «проекция» и все производные от него: проекция точки или фигуры, проецирующая прямая, плоскость проекции и т.д. Почему? Объяснение просто: в основе начертательной геометрии лежит метод проекции.
С понятием проекции мы, не знаем этого, встречаемся постоянно в нашей повседневной жизни. Тень, отброшенная нами на асфальт светом уличного фонаря или морской песок лучами летнего солнца, - это проекция нашей фигуры.
Всякая проекция – отображение, и поэтому для её определения следует ввести три уже известных нам понятия: ЧТО проецируют ( объекты проецирования)?
НА ЧТО проецируют ( плоскость проецирования)?
КАК проецируют (метод проецирования)?
Методы проецирования
Если все лучи проводятся из одной точки (центра) О, то полученное на плоскости проекций изображение называется его центральной проекцией. Форма предмета не искажается, а о размерах судить нельзя. Размеры проекции будут зависеть от расстояния центра проецирования до плоскости проекции.
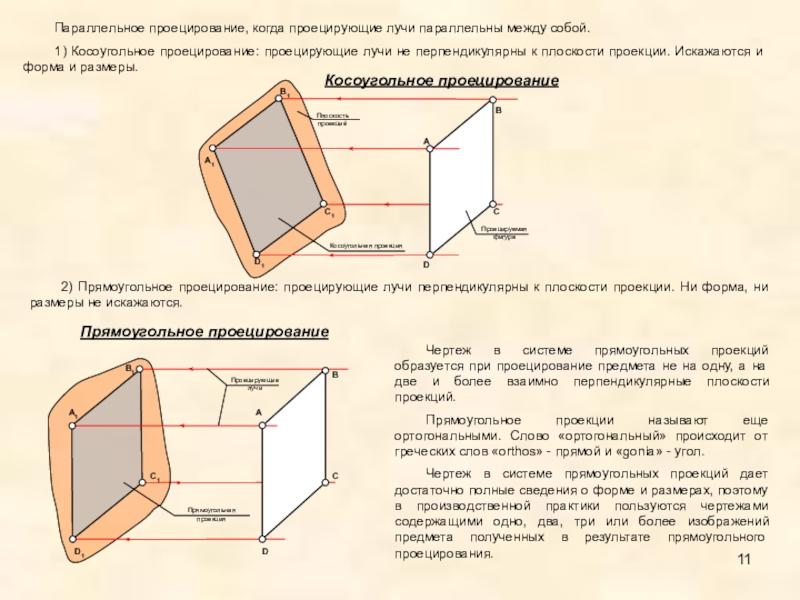
Слайд 11Параллельное проецирование, когда проецирующие лучи параллельны между собой.
1) Косоугольное проецирование: проецирующие
2) Прямоугольное проецирование: проецирующие лучи перпендикулярны к плоскости проекции. Ни форма, ни размеры не искажаются.
Чертеж в системе прямоугольных проекций образуется при проецирование предмета не на одну, а на две и более взаимно перпендикулярные плоскости проекций.
Прямоугольное проекции называют еще ортогональными. Слово «ортогональный» происходит от греческих слов «orthos» - прямой и «gonia» - угол.
Чертеж в системе прямоугольных проекций дает достаточно полные сведения о форме и размерах, поэтому в производственной практики пользуются чертежами содержащими одно, два, три или более изображений предмета полученных в результате прямоугольного проецирования.
Слайд 12О - начало координат.
Х - ось абсцисс (широта).
У - ось ординат
Z - ось аппликат (высота).
В тех, случаях когда по двум проекциям нельзя себе представить форму предмета, его проецируют на три плоскости проекций.
П1 (H) - горизонтальная плоскость проекции.
П2 (V) - фронтальная плоскость проекции.
П3 (W) - профильная плоскость проекции.
П1 ⊥ П2 ⊥ П3 образует октант.
Прямоугольное проецирование
Точка трехмерного пространства, рассуждал Монж, задаётся тремя числами, тремя координатами, каждое из 3-х чисел может быть рассмотрено, как расстояние от какой-нибудь опоры. Чисел три, значит и система опор должна содержать три элемента, и он остановился на трех плоскостях.
Слайд 13
А
В
А1
Проецирование точки на одну
и 2 плоскости проекции
Точка – основной
Каждая точка на плоскости проекций, может быть проекцией множества точек в пространстве, лежащих на одной проецирующей линии. Проекции точек А и В на горизонтальную плоскость П1 совпадают, Это значит что по одному изображению предмета нельзя воспроизводить его пространственный вид, для единственного решения необходимы дополнительные условия.
≡ В1
Точка – это нульмерная фигура по определению Евклида.
Точка есть то, что не имеет измерения.
Для определения положения этих точек А и В в пространстве необходима вторая, (вертикальная) фронтальная плоскость П2, которая определит положение точек А и В по высоте.
В геодезии и в топографии используют метод проекций с числовыми отметками.
Слайд 14
21
28
14
30
7
21
28
14
30
7
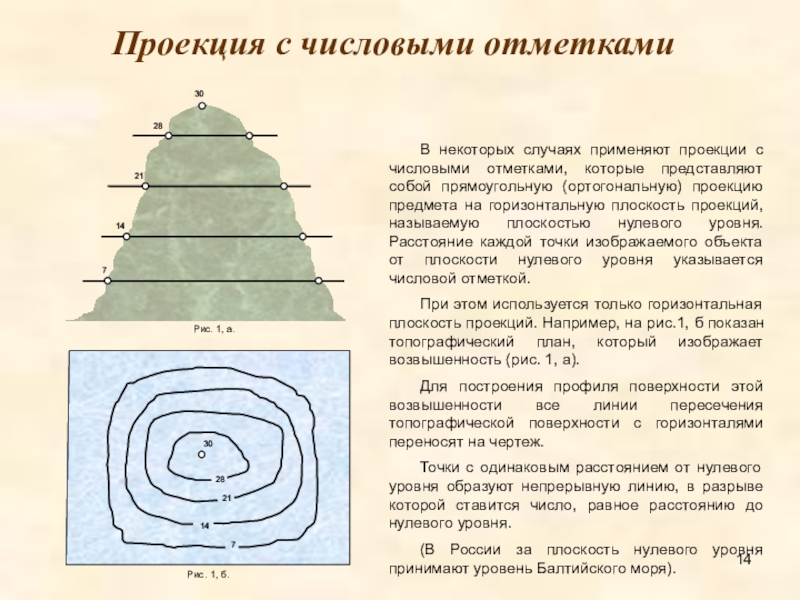
Проекция с числовыми отметками
В некоторых случаях применяют проекции с числовыми отметками,
При этом используется только горизонтальная плоскость проекций. Например, на рис.1, б показан топографический план, который изображает возвышенность (рис. 1, а).
Для построения профиля поверхности этой возвышенности все линии пересечения топографической поверхности с горизонталями переносят на чертеж.
Точки с одинаковым расстоянием от нулевого уровня образуют непрерывную линию, в разрыве которой ставится число, равное расстоянию до нулевого уровня.
(В России за плоскость нулевого уровня принимают уровень Балтийского моря).
Рис. 1, а.
Рис. 1, б.