предметов
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Аксонометрические проекции
Содержание
- 1. Аксонометрические проекции
- 2. Аксонометрические проекции Проецирование предмета на плоскость, при котором
- 3. Применение аксонометрических проекций Аксонометрические проекции применяются для повышения
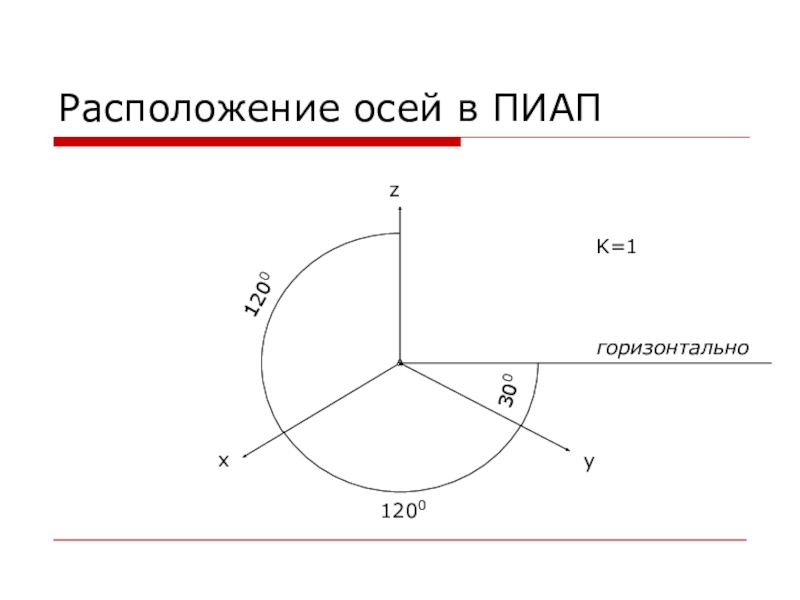
- 4. Прямоугольная изометрическая аксонометрическая проекция (ПИАП) Смысл приставки «изо-» в
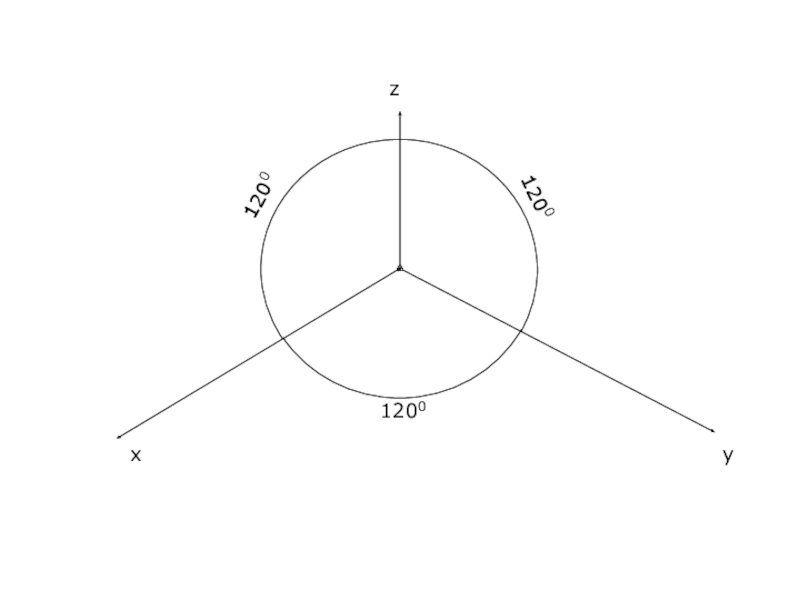
- 5. Расположение осей в ПИАПгоризонтальноzxy12001200300K=1
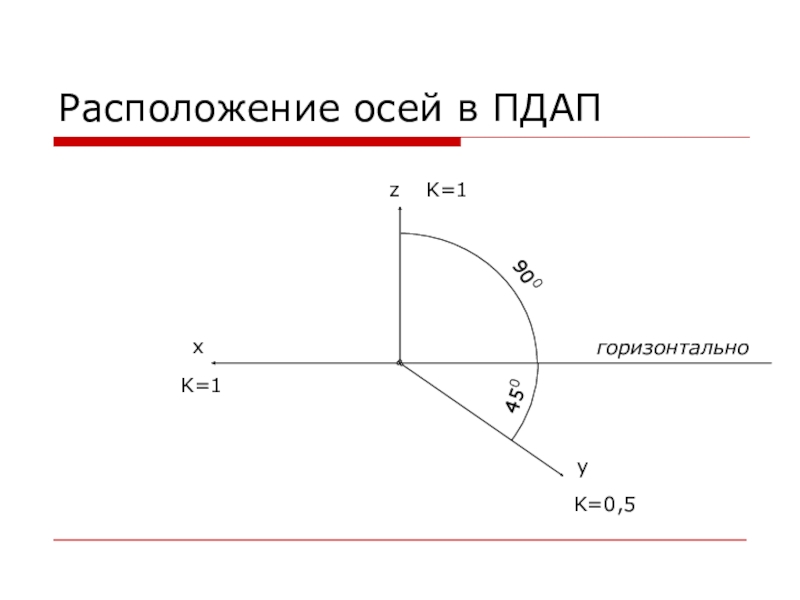
- 6. Прямоугольная диметрическая аксонометрическая проекция (ПДАП) Приставка «ди-» в
- 7. 450Расположение осей в ПДАПгоризонтальноzxy900K=1K=1K=0,5
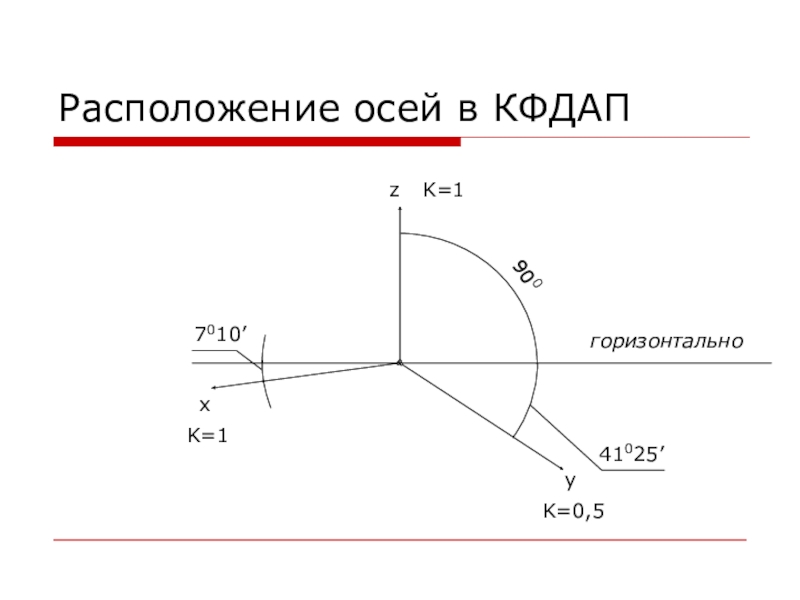
- 8. Косоугольная фронтальная диметрическая аксонометрическая проекция (КФДАП) Исходя из
- 9. 41025’7010’Расположение осей в КФДАПгоризонтальноzxy900K=1K=1K=0,5
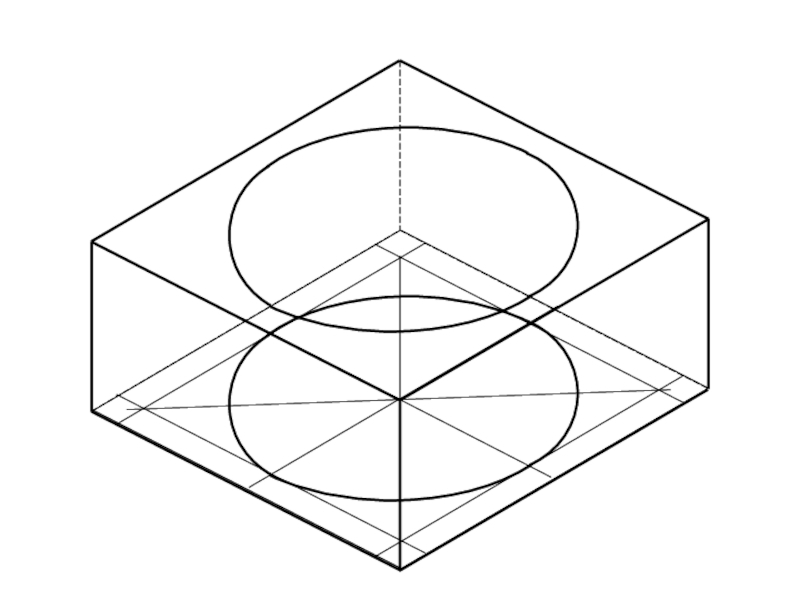
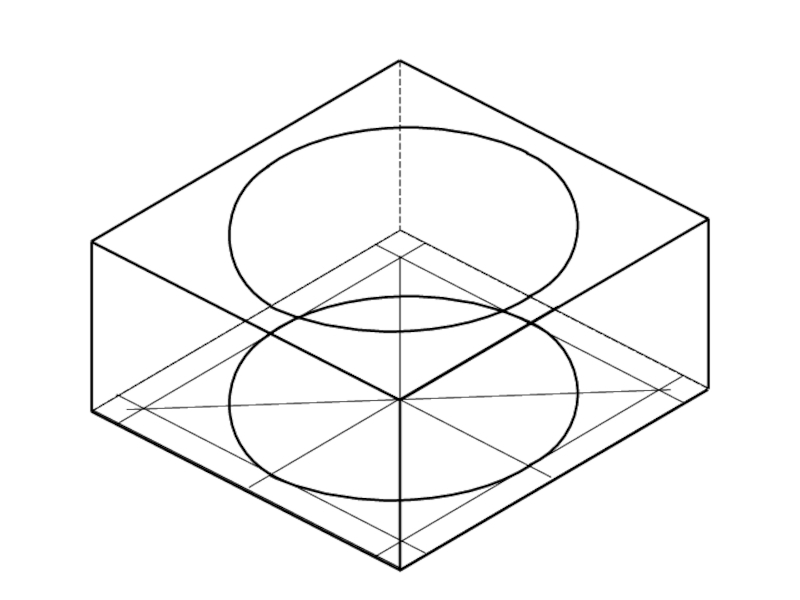
- 10. Искажения в аксонометрических проекциях Окружности в АП изображаются
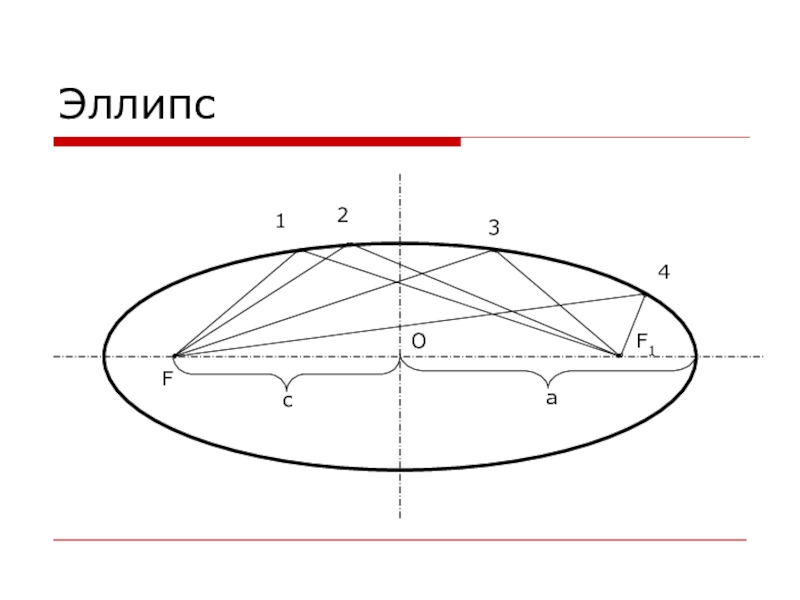
- 11. ЭллипсОFF1ac1234
- 12. Допустимые упрощения Для упрощения построений искаженных окружностей на
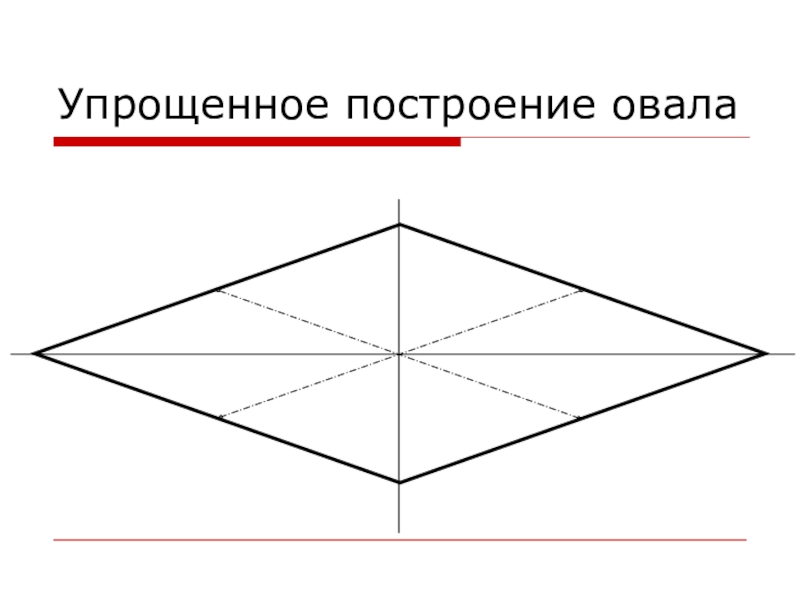
- 13. Упрощенное построение овала
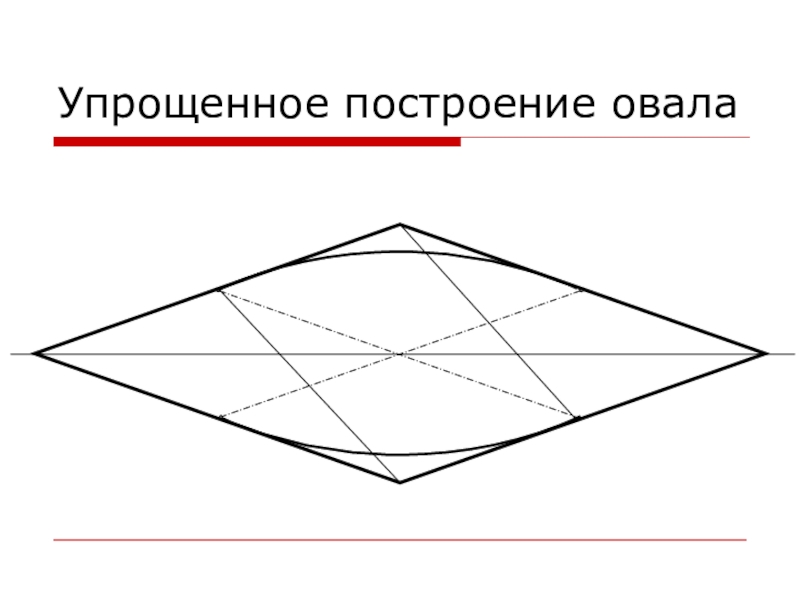
- 14. Упрощенное построение овала
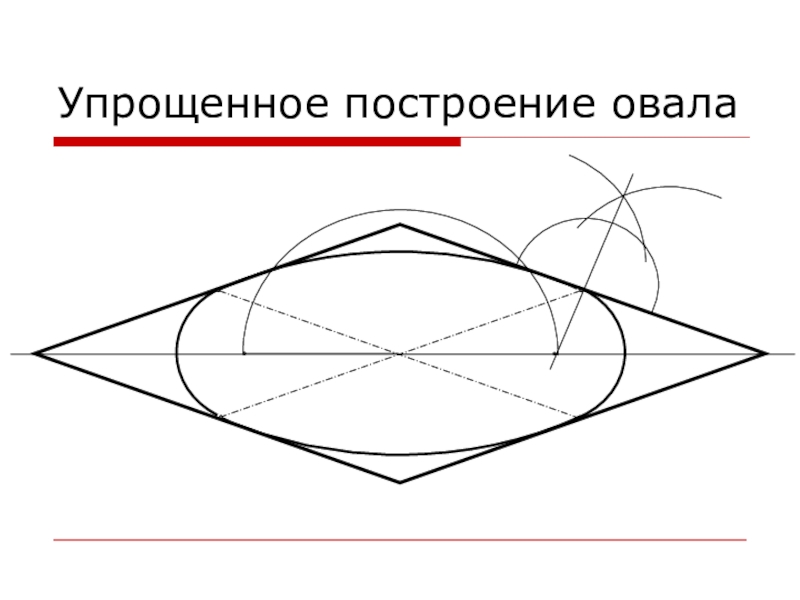
- 15. Упрощенное построение овала
- 16. 120012001200zxy
- 17. zxy
- 18. zxy
- 19. zxy
- 20. zxy
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
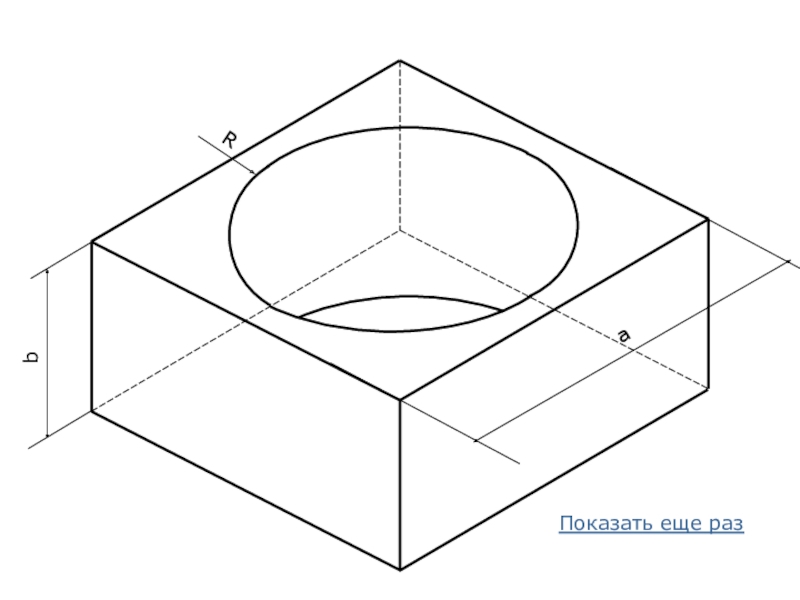
- 27. RПоказать еще разаb
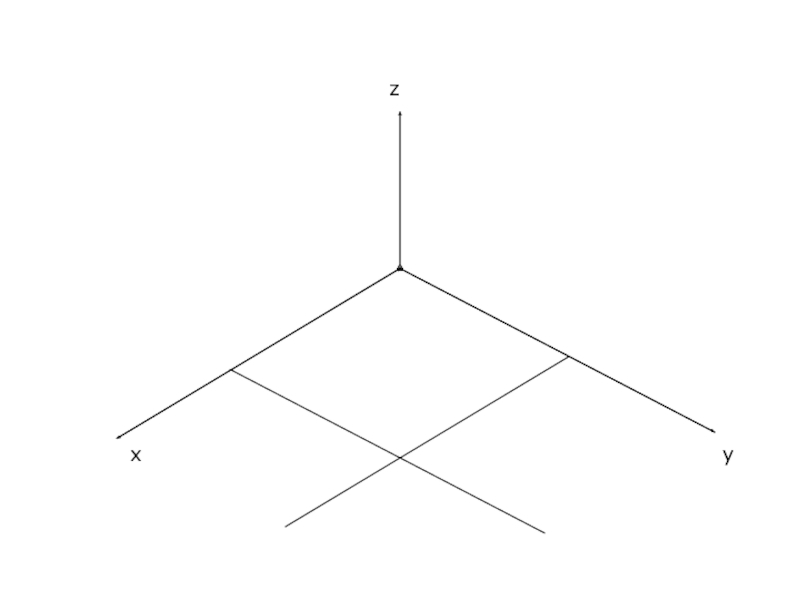
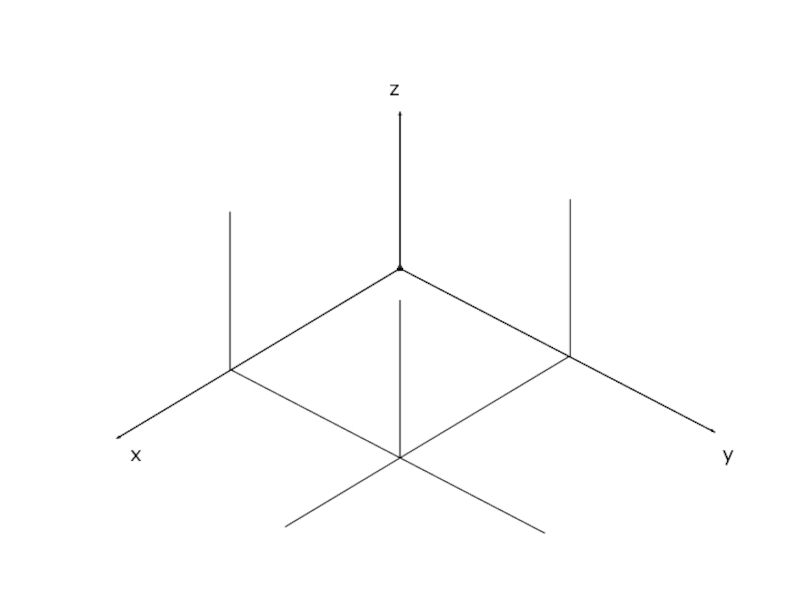
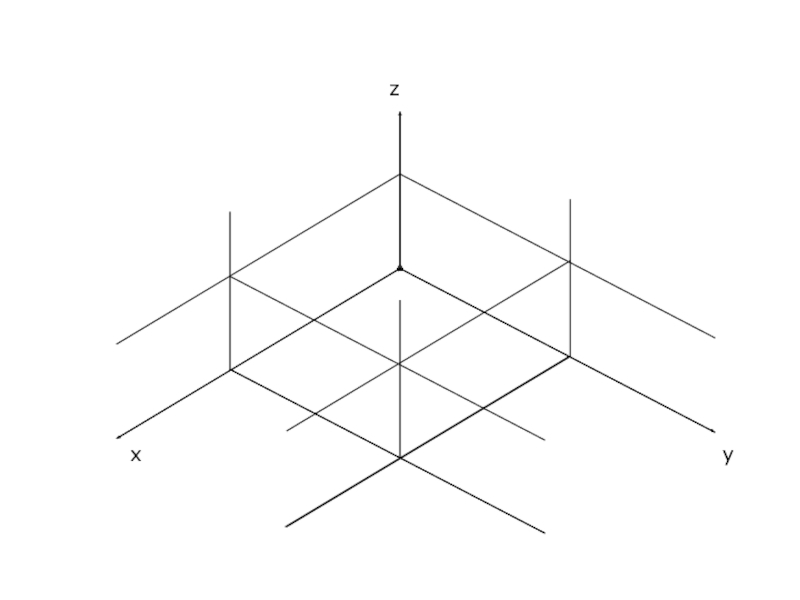
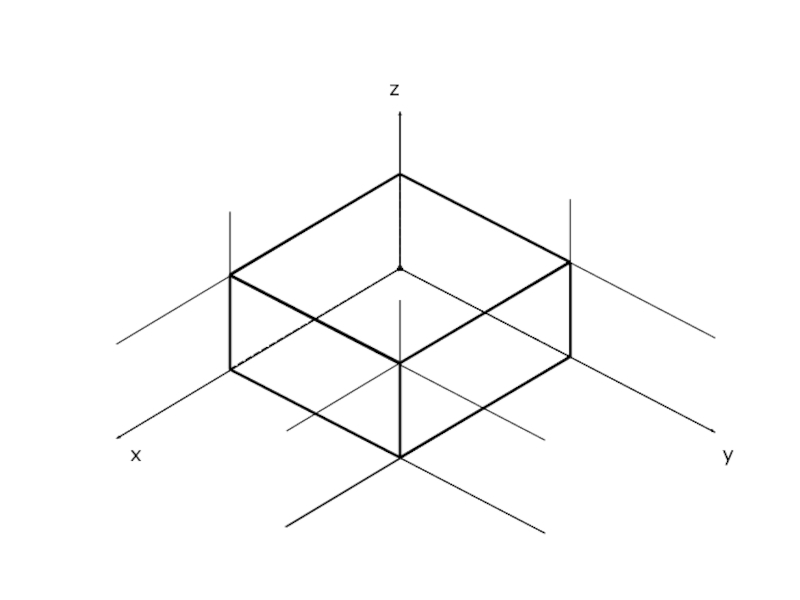
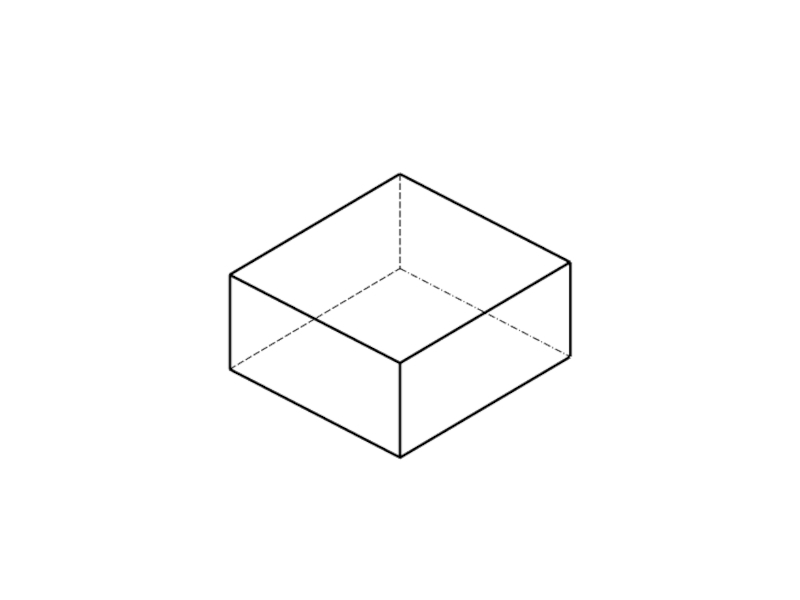
Аксонометрические проекции Проецирование предмета на плоскость, при котором предмет на изображении виден с трех сторон, называется аксонометрическим. Проекции трехмерных объектов на плоскость, получаемые при аксонометрическом проецировании, называются аксонометрическими проекциями
Слайд 1Аксонометрическое проецирование.
Аксонометрические проекции.
Учитель черчения Хоринской СОШ
Евдокимов николай николаевич
Наглядное изображение
Слайд 2Аксонометрические проекции
Проецирование предмета на плоскость, при котором предмет на изображении виден
с трех сторон, называется аксонометрическим.
Проекции трехмерных объектов на плоскость, получаемые при аксонометрическом проецировании, называются аксонометрическими проекциями
Проекции трехмерных объектов на плоскость, получаемые при аксонометрическом проецировании, называются аксонометрическими проекциями
Слайд 3Применение аксонометрических проекций
Аксонометрические проекции применяются для повышения наглядности изображения.
Стандартами рекомендуется применять
3 вида аксонометрических проекций:
Прямоугольная изометрическая проекция
Прямоугольная диметрическая
Косоугольная фронтальная диметрическая
Прямоугольная изометрическая проекция
Прямоугольная диметрическая
Косоугольная фронтальная диметрическая
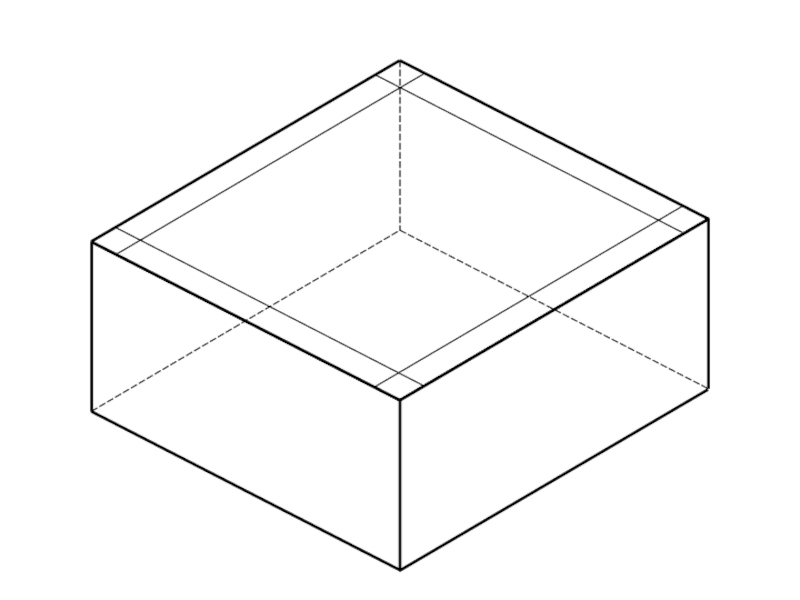
Слайд 4Прямоугольная изометрическая аксонометрическая проекция (ПИАП)
Смысл приставки «изо-» в названии трактуется, как «одинаковый».
Т.е. в изометрической аксонометрической проекции размеры откладываются по всем трем плоскостям с одинаковыми коэффициентами искажения. ГОСТ рекомендует откладывать по всем плоскостям размеры в натуральную величину. В результате изображение получается увеличенным на 18%.
Слайд 6Прямоугольная диметрическая аксонометрическая проекция (ПДАП)
Приставка «ди-» в названии означает «два».
В ПДАП
размеры по осям x и z откладываются без искажений, а по оси y сокращаются в два раза. При этом изображение получается увеличенным на 6%
Слайд 8Косоугольная фронтальная диметрическая аксонометрическая проекция (КФДАП)
Исходя из названия в КФДАП используется
не прямоугольная система координат, а косоугольная.
Слово «диметрическая» означает, что коэффициент искажения по двум («ди-») осям одинаков.
По сути, КФДАП – уточненный вариант ПДАП. Но при построении предмета на осях КФДАП его изображение практически не увеличивается
Слово «диметрическая» означает, что коэффициент искажения по двум («ди-») осям одинаков.
По сути, КФДАП – уточненный вариант ПДАП. Но при построении предмета на осях КФДАП его изображение практически не увеличивается
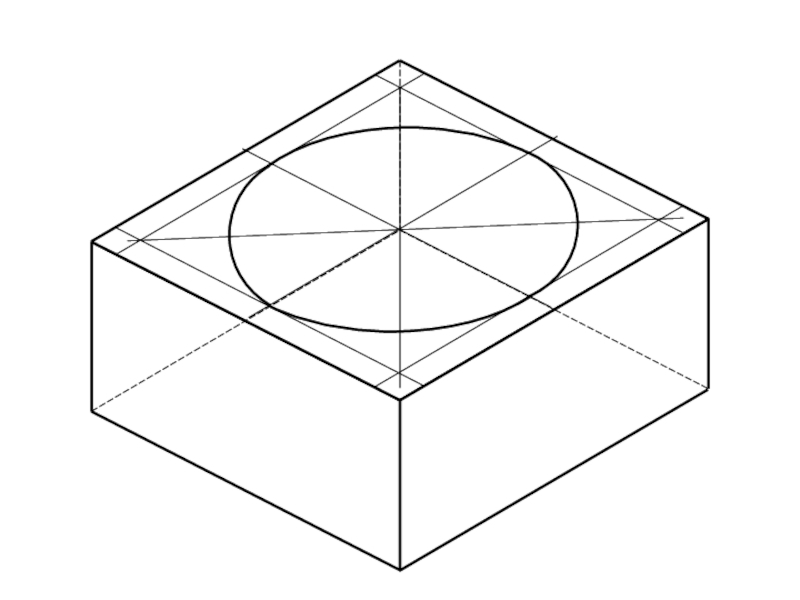
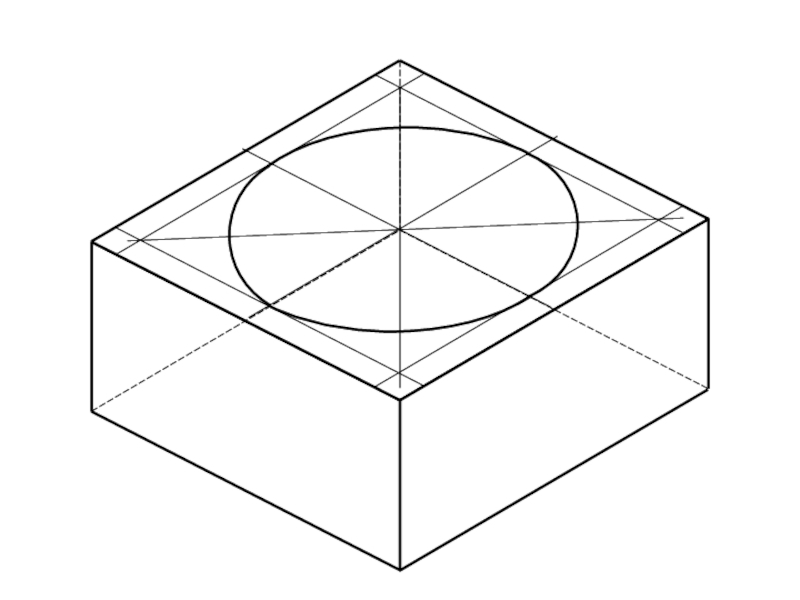
Слайд 10Искажения в аксонометрических проекциях
Окружности в АП изображаются в виде эллипсов.
Эллипс
– геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек F и F1 той же плоскости есть величина постоянная и равная 2a.
Точки F и F1 называются фокусами.
Эллипс имеет две оси – большую и малую. Точка пересечения осей – центр эллипса, точка О. Расстояние между фокусами, равное 2с, называется фокусным расстоянием
Точки F и F1 называются фокусами.
Эллипс имеет две оси – большую и малую. Точка пересечения осей – центр эллипса, точка О. Расстояние между фокусами, равное 2с, называется фокусным расстоянием
Слайд 12Допустимые упрощения
Для упрощения построений искаженных окружностей на изометрической проекции (и только
на ней!) допускается вместо эллипсов использовать овалы.
Овал – выпуклая замкнутая плоская кривая, образованная сопряженными дугами окружностей разных радиусов
Овал – выпуклая замкнутая плоская кривая, образованная сопряженными дугами окружностей разных радиусов