- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Развитие творческих способностей обучающихся в математике
Содержание
- 1. Презентация Развитие творческих способностей обучающихся в математике
- 2. Общие цели школьного образования На современном
- 3. Компетентности, формируемые у обучающихся «Умение учиться».«Умение объяснять
- 4. «Умение учиться» … Освоение источников образовательной информации:
- 5. «Умение объяснять явления действительности» Круг решаемых проблем,
- 6. «Умение ориентироваться в мире ценностей» …Умение сравнивать
- 7. «Умение решать проблемы, связанные с выполнением человеком
- 8. «Ключевые навыки» (применимые в разных сферах и
- 9. «Способность ориентироваться в мире профессий, ситуации на
- 10. Развитие творческих способностей обучающихся в математике и
- 11. Мышление - высшая способность человеческого мозга отражать
- 12. Формирование и развитие критического мышления Приглашать
- 13. Преимущества техник по развитию критического мышленияУченик на
- 14. Аргументы Харви Зигеля в пользу продвижения критического
- 15. «Математика является меньше знанием, чем умением»Сервэ.
- 16. Этапы формирования компетенцийВызов.Осмысление.Размышление.Экстенсия.
- 17. ВызовСоздается контекст, в котором обучающийся вспоминает, что
- 18. ОсмыслениеОбучающийся входит в контакт с новыми сведениями
- 19. РазмышлениеНа этом этапе преследуются несколько важных моментов:Создание
- 20. ЭкстенсияНа этом этапе становится очевидной соотнесенность теории
- 21. Мотивационный этап. Условия, необходимые для успешной учебной
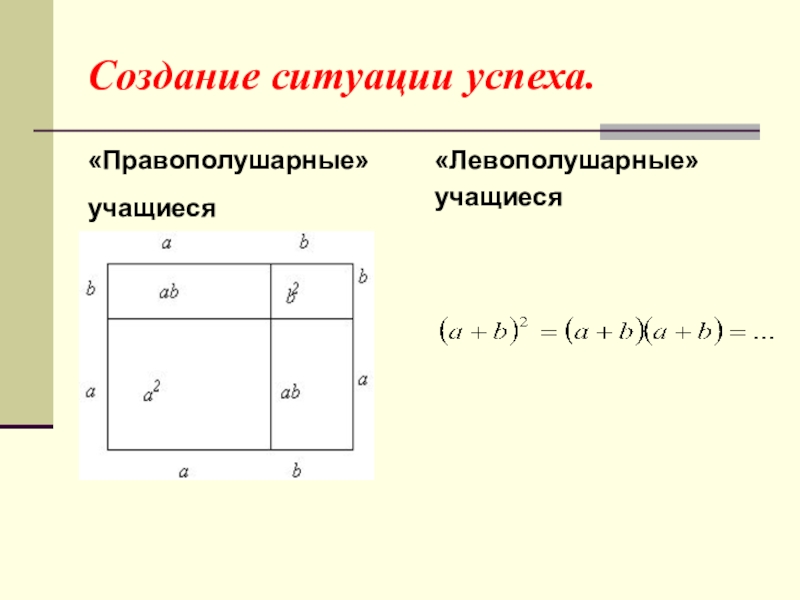
- 22. Создание ситуации успеха.«Правополушарные»учащиеся «Левополушарные»учащиеся
- 23. Основные языки, широко используемых в процессе обучения
- 24. АГ требуют перевода с аналитического языка на
- 25. «Как развивать графическое мышление» Необходимость указанного
- 26. Восприятие материалаЦелостное.Интонационная сторона речи.Визуалисты (зрительное). Математическая разминка:
- 27. Выход математики на одно из ведущих мест
- 28. Примеры задач и заданий (1) практика.1.«Физиологические функции
- 29. Примеры задач и заданий (2) производство.Вход в
- 30. Примеры задач и заданий 3) социально-экономической практике.
- 31. «Математика, будучи фундаментальной теоретической наукой, на многих
- 32. «Математика имеет свои неповторимые возможности для формирования
- 33. Конструирование математических моделейСхема приложения теории к практике
- 34. Еще несколько задач, решаемых математическим моделированием:Что бы
- 35. Показ межпредметных целей развития наукиНаложение центров тяжести
- 36. Показ диалектического единства математикиПоложительные числа удовлетворяют системе уравненийВычислить величину
- 37. Принципы отбора содержания математического содержания:Конкретность материала, используемого
- 38. Организация учебного-воспитательного процесса, направленного на развитие творческих
- 39. Случай развития межпредметной компетенции в рамках ситуации,
- 40. Приёмы сообщения информации и демонстрацииУрок-викторина «А.С. Пушкин
- 41. Упражение как средство развития и приобретения свойств
- 42. Групповые формы работы обучающихсяНапример, техника «Мозговой штурм»,
- 43. Побуждающее-исследовательские, информационно-поисковые методы обученияПредлагаю учащимся провести биссектрису
- 44. Вопросы моих учеников важны для меняИсследовательская работа
- 45. «А где я могу применить эти полученные
- 46. Создание ситуации заинтересованности учащихся к поставленной проблеме«Как с помощью шкуры быка заполучить царство?»«Нестандартное решение задач оптимизации».
- 47. Результат учебного исследования -для учащихся - достижение
- 48. Нет детей одаренных и нет не одаренныхЕсть
- 49. Высказывания учеников:«Математика – наука интересная,
- 50. Юные исследователи – математики, 40-й городской конференции
Слайд 1«Записки старого человека»
А.П. Чехов
«Будущность его представляется мне ясно.
Слайд 2Общие цели школьного образования
На современном этапе развития общества необходимо
Слайд 3Компетентности, формируемые у обучающихся
«Умение учиться».
«Умение объяснять явления действительности».
«Умение ориентироваться в
«Умение решать проблемы, связанные с выполнением человеком определенной социальной роли».
«Ключевые навыки» (применимые в разных сферах и видах деятельности).
«Способность ориентироваться в мире профессий, ситуации на рынке труда и образовательных услуг в сфере профессионального образования».
Слайд 4«Умение учиться»
…
Освоение источников образовательной информации: учебная литература, аутентичные тексты (научная,
…
Слайд 5«Умение объяснять явления действительности»
Круг решаемых проблем, описание и объяснение явлений действительности,
…
Умение выделять существенные и несущественные признаки изучаемых явлений, устанавливать причинно-следственные связи между явлениями, выявлять тенденции, выдвигать гипотезы…
…
Слайд 6«Умение ориентироваться в мире ценностей»
…
Умение сравнивать разные взгляды на одни и
…
Слайд 7«Умение решать проблемы, связанные с выполнением человеком определенной социальной роли»
Круг решаемых
Теоретические основы образовательной деятельности: научные понятия изучаемых учебных дисциплин, которые возможно использовать при анализе конкретных жизненных ситуаций.
…
Слайд 8«Ключевые навыки» (применимые в разных сферах и видах деятельности)
Круг решаемых проблем:
Коммуникативные навыки, навыки работы с информацией, навыки измерений, навыки совместной деятельности, навыки принятия решений, навыки исследовательской и проектной деятельности.
…
Слайд 9«Способность ориентироваться в мире профессий, ситуации на рынке труда и образовательных
…
Исследовательские умения.
…
Слайд 10Развитие творческих способностей обучающихся в математике и важнейшие цели математического образования
Воспитание
Воспитание эстетического чувства.
Способствование формированию важнейших интеллектуальных умений и мышления, способностей ума.
Формирование сознания.
Сознание – это со-знание.
Мышление – это умение, то есть способность использовать имеющиеся знания. И умение подразумевает: независимость мышления, изобретательность, творческие способности.
Слайд 11Мышление - высшая способность человеческого мозга отражать в обобщенном виде объективную
Логическое мышление представляет собой систему форм и отражающих законов, признанных верными, правильными. Формируется в три этапа: спонтанное, осознанное, контролируемое.
Креативное мышление выражается в осязаемом/видимом результате. Оно соотносится с результатом.
Аналитическое мышление – это мыслительная способность разделять составные части единого целого, отвечая на вопросы ЧТО? КАКОЙ? Оно не производит ничего нового, а только устанавливает различия.
Синтетическое мышление отвечает на вопрос ЧТО ПРОИЗОШЛО НА САМОМ ДЕЛЕ? Строит связующие мосты, производит нечто новое.
Вертикальное мышление требует осуществления последовательных шагов, приближающих нас к результату при анализе релевантной информации; каждый последующий шаг должен находить свое обоснование в предыдущем.
Латеральное или боковое мышление представляет собой процесс, характерный для креативного мышления, и ставит целью приобретение как можно большего числа возможных вариантов исследуемого предмета или явления. Оно соотносится с процессом. Используем информацию для того, чтобы в конечном итоге прийти к правильному решению.
Рефлексивное мышление (метакогниция), будучи однажды сформированным, позволяет размышлять над развитием своих познавательных способностей, контролировать собственные мыслительные операции, мыслить о собственном мышлении.
Критическое мышление – это способность ученика обрабатывать идеи, для того чтобы выстроить систему знаний и ценностей. Согласно таксономии Блума, операции критического мышления располагаются на высших ступенях: анализ, синтез, оценивание. Проходит этапы понимания, воплощения, интерпретации, применения.
Слайд 12Формирование и развитие критического мышления
Приглашать обучающегося мыслить критически -
Слайд 13Преимущества техник по развитию критического мышления
Ученик на протяжении всего урока находится
Ученик перенимает на каждом уроке новый опыт обучения.
Ученик организует свою интеллектуальную деятельность.
Ученик осуществляет самооценивание и взаимное оценивание, что внесет несомненный вклад в формирование личного интеллектуального стиля.
Учитель становится стратегом.
Слайд 14Аргументы Харви Зигеля в пользу продвижения критического мышления (к.м.):
Практика к.м. требует
К.м. развивает независимость мышления;
К.м. активизирует ряд предрасположений, установок и навыков;
К.м. является существенным условием для жизни в демократическом обществе.
Слайд 17Вызов
Создается контекст, в котором обучающийся вспоминает, что ему известно по данной
Слайд 18Осмысление
Обучающийся входит в контакт с новыми сведениями или идеями. В это
Слайд 19Размышление
На этом этапе преследуются несколько важных моментов:
Создание условий для того, чтобы
Способствование возникновению здорового обмена идеями между обучающимися, посредством которого развивается их словарный запас и способность к выражению своих мыслей. Обучающиеся сталкиваются с разнообразием моделей мышления.
Создание контекста для выражения отношений к изучаемому материалу.
Слайд 20Экстенсия
На этом этапе становится очевидной соотнесенность теории и практики. Обучающиеся осуществляют
Слайд 21Мотивационный этап.
Условия,
необходимые
для успешной учебной деятельности.
«Правополушарные»
учащиеся
Образы.
Контекст.
Связь информации с реальностью, практикой.
Творческие задания.
Эксперименты.
Музыкальный
Речевой и музыкальный ритм.
«Левополушарные»
учащиеся
Технология.
Детали.
Абстрактный линейный стиль изложения информации.
Неоднократное повторение учебного материала.
Тишина на уроке.
Слайд 23Основные языки, широко используемых в процессе обучения математике:
естественный, словесный язык (С);
язык аналитических выражений (А);
язык графических изображений, «графический язык» (Г). При решении задач графического содержания возникает необходимость осуществлять преобразование входной информации (условия задач) с языка, на котором она была задана, на язык, предполагаемый в ответе к задаче. Задачи графического содержания в соответствии с возможным сочетанием языков выражения условия и ответа разбиваются на пять классов. (Первая буква в обозначении класса показывает язык, на котором выражено условие задачи, а вторая – язык, на котором должен быть выражен ответ.)
1).СГ – словесное описание – графический образ;
2).АГ – аналитическое описание – графический образ;
3).ГС – графический образ – словесное описание;
4).ГА – графический образ – аналитическое описание;
5).ГГ – графический образ – графический образ.
Слайд 24АГ требуют перевода с аналитического языка на язык графических образов.
Они способствуют
Слайд 25«Как развивать графическое мышление»
Необходимость указанного подхода определяется общетеоретическими положениями
Слайд 26Восприятие материала
Целостное.
Интонационная сторона речи.
Визуалисты (зрительное).
Математическая разминка: в парах дать оценку
Дискретное (по частям).
Смысловая сторона речи.
Аудисты (слуховое).
Задача: «Построить график функции, «описывающей поговорку «Глубоко нырнул, да вынырнуть не может!»»
Слайд 27Выход математики на одно из ведущих мест в системе научных знаний
1) практике;
2) производстве;
3) социально-экономической практике.
Слайд 28Примеры задач и заданий (1) практика.
1.«Физиологические функции человека строятся на основе
Кто знает, сколько воды в среднем (в кг) приходится на взрослого человека? (На 70 кг массы тела приходится 50 кг воды или … )»
Приглашается желающий учащийся взвеситься и вычислить, сколько кг воды приходится на массу его тела. Какое соответствие установлено между массой тела и количеством воды?
2. «Вода необходима не только человек, но и всей живой и неживой природе.
Назовите самые древние растения на Земле (водоросли).
Их существует около 30 тыс. видов, им мы обязаны кислородом, которым мы дышим. Водоросли устойчивы к неблагоприятным условиям, живут в среде от +100º до -200ºС, но выдерживают лишь в воде: на 1л-300г соли.
Посчитайте, сколько % составляет соль в таком растворе? (в паре, к доске приглашается учащийся, пожелавший отвечать)».
3. Вам подарили золотую рыбку, которая может жить в 6% растворе соли. Сколько необходимо взять дистиллированной воды, чтобы растворить 750г соли?
4.Вы хотите развести в аквариуме зеленые водоросли, при этом необходимо очень экономно отнестись к расходованию воды, имея 330г 40% раствора соли.
Какое наименьшее количество воды вы используете?».
5. Наложение центров тяжести треугольника, найденных практически (физика) и аналитически (математически).
Вершины треугольника: Масштаб:1 ед.=5 см.
Слайд 29Примеры задач и заданий (2) производство.
Вход в ангар для самолетов имеет
Необходимо покрыть жестью часть крыши, имеющей форму фигуры, ограниченной графиками функций Масштаб: 1 ед.=1 м. Хватит ли 4 м2 жести для покрытия этой части крыши?
Печатный текст (вместе с межстрочным интервалом) одной страницы книги должен занимать см2. Ширина верхних и нижних полей страницы равна а см, а боковых полей – b см. Какими должны быть размеры страницы, чтобы расход бумаги на изготовление книги был наименьшим?
Количество краски достаточно, чтобы покрасить шар диаметром 24 см. Сколько шаров радиуса 4 см можно покрасить тем же количеством краски, если толщина слоя краски у всех шаров одинакова?
Для транспортировки строительных материалов два здания соединены наклонным желобом. Его концы находятся на расстоянии 4 м и 12 м от поверхности земли. Найдите длину желоба, если известно, что расстояние между зданиями равно 15 м.
Длина стальной шины при температуре 00С равна 50 м. Известно, что длина l этой шины меняется в зависимости от температуры по закону На сколько сантиметров изменится длина шины при изменении температуры от 200С до 500С?
Склад имеет форму полусферы. Сколько килограммов краски необходимо для окрашивания наружной поверхности склада, если на покраску пола потребовалось 50 кг?
Из листа жести прямоугольной формы изготовили информационную тумбу в виде цилиндра. Внутри ее укрепили металлическим каркасом по форме осевого сечения цилиндра. Высота каркаса 2 м, а ширина – 1,5 м. Достаточно ли 3 кг краски для окрашивания тумбы снаружи. Если на 1 м2 поверхности расходуется 400 г? При вычислениях округлите число до целых.
Крыша дома имеет форму пирамиды, в основании которой лежит прямоугольник со сторонами 8 м и 10 м. Высота пирамиды равна 3 м. Хозяин намерен покрыть поверхность крыши черепицей. А по боковым ребрам – выложить кант. Зная, что 1 м2 черепицы стоит 400 рублей, а 1 м канта – 450 рублей, определите сумму, необходимую для приобретения кровельных материалов. В вычислениях можно использовать округления.
Слайд 30Примеры задач и заданий 3) социально-экономической практике.
1. Длина комнаты Юли 4,5
2. Супермаркет провел акцию, в результате которой дважды на 10% понижались цены на мобильные телефоны. Сколько стоил мобильный телефон по завершению акции, если первоначальная его цена 4000 рублей?
3. Фирма арендует под офис три одинаковых помещения, каждое по 6 м в длину и по 4,5 м в ширину. Ежемесячная плата за 1 м2 составляет 6 у.е. Какова арендная плата за год?
4. Из стального шара радиуса 17 см изготовили, с наименьшим количеством отходов, деталь в виде прямого кругового конуса. Найдите объем изготовленной детали.
5.Хозяин автостоянки, общей площадью в 300 м2, предлагает клиентам места площадью 10 м2 для легковых автомобилей и 30 м2 для грузовых автомобилей. Максимальное количество автомобилей, которое можно разместить на автостоянке, равно 20, причем легковых автомобилей должно быть не меньше грузовиков. Стоимость стоянки для легкового автомобиля составляет 15 рублей в сутки, для грузовика – 17 рублей. Постройте таблицу для решения задачи. Используя данные заполненной таблицы, определите, сколько автомобилей каждого вида можно ежесуточно разместить на автостоянке, чтобы ее хозяин получил максимальную прибыль.
Слайд 31«Математика, будучи фундаментальной теоретической наукой, на многих важных этапах своего развития
А.Н. Земляков
Слайд 32«Математика имеет свои неповторимые возможности для формирования правильных взглядов на научное
Б.В. Гнеденко
Слайд 33Конструирование математических моделей
Схема приложения теории к практике осталась традиционной:
Реальная задача –
Характерны следующие взаимосвязанные моменты и тенденции:
Расширился класс научных и практических задач, к которым применимы математические методы исследований.
Обогатились сами методы математического моделирования.
Расширились возможности практических приложений математических моделей и экспериментов (ЭВМ).
Слайд 34Еще несколько задач, решаемых математическим моделированием:
Что бы вы предпочли: съесть арбуз
Клоун выступает в колпаке в форме конуса, радиус основания которого 9 см, а высота 12 см. Во время представления клоун наливает в колпак всю воду из полной бутылки емкостью 1 л. Наполнится ли колпак этим количеством воды?
Из одного и того же порта одновременно вышли два сухогруза: один в южном направлении, а другой в западном. Первый двигался со скоростью 4 км/ч, а другой – 5 км/ч. Спустя некоторое время первый сухогруз удалился от порта на 7 км, - на 10 км. Через сколько часов расстояние между сухогрузами составит 25 км?
Для транспортировки строительных материалов два здания соединены наклонным желобом. Его концы находятся на расстоянии 4 м и 12 м от поверхности земли. Найдите длину желоба, если известно, что расстояние между зданиями равно 15 м.
Эпицентр циклона, движущегося прямолинейно, при первом измерении находился в 24 км севернее и в 5 км западнее метеорологической станции. При втором измерении эпицентр циклона находился в 20 км севернее и в 3 км западнее станции. Определите наименьшее расстояние сближения циклона со станцией.
Две взаимно перпендикулярные автодороги делят территорию на четыре части, в одной из которых расположено здание фабрики на расстоянии 1 км и 8 км от каждой из этих дорог. Минуя перекресток, надо проложить прямолинейный путь минимальной протяженности, соединяющий фабрику с каждой из пересекающихся автодорог. Определить длину этого пути.
Глубина стаканчика (конической формы) для мороженого равна 12 см, а диаметр его верхней части равен 5 см. В него сверху положили шарик мороженого радиусом 2,5 см. Переполнит ли мороженое стаканчик, если позволить ему растаять?
Из города В в город А в 5 ч 30 мин вылетел самолет. В 8 ч 30 мин из А в В вылетел вертолет. Скорости самолета и вертолета на всем пути постоянные, и они летят по одной трассе. После их встречи вертолет прибыл в В через 9 ч, а самолет прибыл в А через 2 ч. Найти время прибытия самолета в город А.
Слайд 35Показ межпредметных целей развития науки
Наложение центров тяжести треугольника, найденных практически (физика)
Вершины треугольника: Масштаб:1 ед.=5 см.
Демонстрирую физический опыт: «Возьмите проволочное колечко, окуните его в мыльный раствор и осторожно положите на образовавшуюся плёнку связанную кольцом нитку (не забудьте сначала смочить её в том же растворе, иначе плёнка лопнет). Нитка лежит петлёй неправильной формы. А теперь проколите плёнку внутри нитяной петли». Чтобы понять, почему петля приобретает форму именно окружности, приглашаю учеников прочитать главу «Задача Дидоны» в разделе математика детской энциклопедии «Я познаю мир» и изучить свойства числовых неравенств.
Слайд 36Показ диалектического единства математики
Положительные числа удовлетворяют
Вычислить величину
Слайд 37Принципы отбора содержания математического содержания:
Конкретность материала, используемого при изучении абстрактных математических
Сочетание современного методического и конкретно-исторического подходов при изучении математических теорий и их приложений.
Демонстрация практических приложений математики, показ межпредметных целей развития науки.
Отражение в преподавании межнаучных связей – осуществление межпредметных связей в качестве методического средства.
Последовательная реализация внутриматематических связей, показ диалектического единства математики.
Использование наглядности как средства формирования, сознательного и устойчивого восприятия теоретических знаний.
Привлечение систематизации задач на основе их классификации в целях формирования устойчивых, систематических навыков в решении математических задач, обучение методам решения задач.
Преемственность в обучении, единство изучения математики с общеобразовательным курсом.
Слайд 38Организация учебного-воспитательного процесса, направленного на развитие творческих способностей и навыков исследовательской
Преподавание – пре-подавание – начинается тогда, когда мы начинаем ощущать, воспринимать предмет сердцем, глазами ученика.
Слайд 39Случай развития межпредметной компетенции в рамках ситуации, созданной самим учеником.
В условиях
Слайд 40Приёмы сообщения информации и демонстрации
Урок-викторина «А.С. Пушкин и математика», проведённый в
«... Но провидение не алгебра. Ум человеческий, по простонародному выражению, не пророк, а угадчик, он видит общий ход вещей и может выводить из оного глубокие предположения, часто оправданные временем, но невозможно ему предвидеть случая – мощного мгновенного орудия провидения...».
А.С. Пушкин
Слайд 41Упражение как средство развития и приобретения свойств и качеств личности, необходимых
Творческие работы: например, придумать квадратное уравнение, несколькими способами решить его, а затем сделать проверку полученного решения, используя известные им методы. Этот метод можно назвать методом организации самостоятельной поисковой деятельностью учащихся (эвристической и исследовательской).
Слайд 42Групповые формы работы обучающихся
Например, техника «Мозговой штурм», когда наработанные решения часто
Слайд 43Побуждающее-исследовательские, информационно-поисковые методы обучения
Предлагаю учащимся провести биссектрису угла односторонней линейкой.
Возвращаюсь
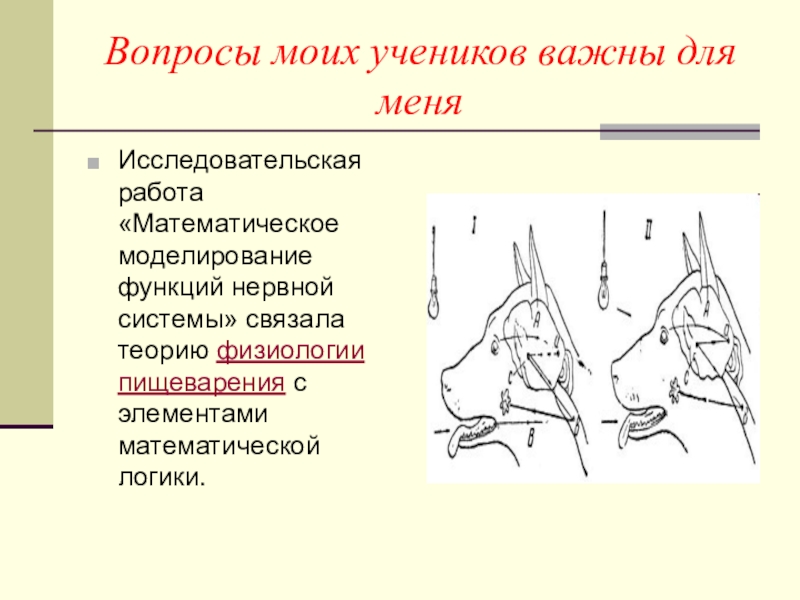
Слайд 44Вопросы моих учеников важны для меня
Исследовательская работа «Математическое моделирование функций нервной
Слайд 45«А где я могу применить эти полученные знания?»
«Фракталы и комплексные числа».
«Физические
«Во всём мире есть множество интересных парадоксов и феноменов. Множество из них были доказаны и объяснены наукой. Благодаря фракталам, человечество может создавать 3D-модели разных объектов или регионов. Скажем, карты с точным рельефом, детализация которых может быть очень приближена к реальности. Также можно, используя комплексные числа, создавать примерные модели клеток живого организма. Или даже предсказывать поведение цен акций на экономических биржах».
«Мы любим стабильность и точность, и если мы не можем найти их в повседневной жизни, то пытаемся найти в математике. Математика – точная наука, и в тоже время в ней есть над чем подумать».
Слайд 46Создание ситуации заинтересованности учащихся к поставленной проблеме
«Как с помощью шкуры быка
«Нестандартное решение задач оптимизации».
Слайд 47Результат учебного исследования -
для учащихся - достижение субъективной истины, движение к
для учителя -накопление научно-методологического материала, дальнейший профессиональный рост, ведь внутренняя мотивация и интерес к проблеме исследования у самого педагога – основа успеха реализации деятельности учащимся.
Слайд 48Нет детей одаренных и нет не одаренных
Есть те, кого правильно обучали
«Нет плохих учеников, есть плохие учителя»:
Слайд 49Высказывания учеников:
«Математика – наука интересная,
Дарит знания,
В школе очень нужная, полезная,
Открывает мир мечты и дум.
Этот мир богат задачами, примерами,
Сколько формул, действий, теорем.
Не в деньгах мы будем миллионерами –
Открывателями новых идей и тем.
Долго думали над этим обстоятельством,
И учитель вдруг заметил нас,
Удивили мы его талантом, качеством,
И в способностях мы показали класс!»
«Мы живём в мире, где очень много сомнений и неясностей. Если сегодня ты живёшь в достатке и благополучии, то нет никакой уверенности, что завтра ты всего этого не потеряешь. Нельзя сказать, что математика – это шаблон, нет, и мы это доказали в своей работе, где рассмотрели интересные способы решения уравнений и неравенств, которые не изучаются в школьной программе.
Было интересно узнать, что если использовать свойство монотонности функций, очень сложное на первый взгляд, уравнение можно упростить до простейшего, которое может решить любой пятиклассник. И именно это свойство может помочь нам в дальнейшем, ведь знание некоторых особенностей даёт нам преимущество перед сверстниками при решении такого типа уравнений.
Участие в конференции и получение диплома подбодряют нас и настраивают на дальнейшие исследования, и, пусть маленькие, но всё же открытия, в первую очередь для самих себя». Рахимова Т. и Гончаренко А.