Выполнила: Кузнецова Татьяна,
обучающаяся 9-а класса
Руководитель: Львова Светлана Юрьевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательская работа Математика в архитектуре Путевого дворца
Содержание
- 1. Исследовательская работа Математика в архитектуре Путевого дворца
- 2. Тверской Путевой дворецВладельцы усадьбы: 1766 – нач.
- 3. МАТЕМАТИКА В АРХИТЕКТУРЕКогда я услышала словосочетание «математика
- 4. Слайд 4
- 5. Слайд 5
- 6. ГипотезаМногим трудно поверить, что искусство может свободно
- 7. История Путевого Дворца Дворец с двумя павильонами был
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. АрхитектураАрхитектура – древнейшая сфера человеческой деятельности («искусство
- 14. Связь математики и архитектурыФундаментальные закономерности математики являются
- 15. Виды симметрии:В архитектуре часто используются разные виды
- 16. Как математика помогает планировать архитектурные объектыПри составлении
- 17. Как математика помогает добиться прочности сооруженийПрочность зданий
- 18. Переносная симметрия обычно используется при построении бордюров.
- 19. Крестообразные купола в основании павильоны на концах
- 20. Ампирные фасады дополнились наличниками, рустовками, тягами, филенками
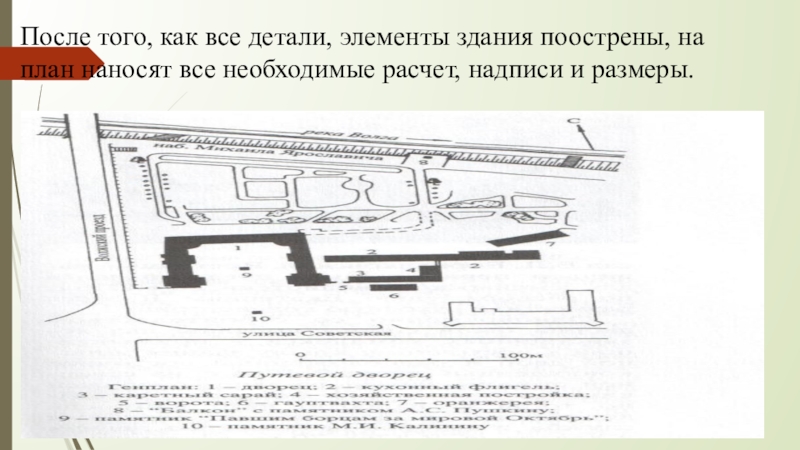
- 21. После того, как все детали, элементы здания
- 22. Итак, математические расчеты, измерения, построения – это самые важные и незаменимые методы для архитектора
- 23. Слайд 23
- 24. Слайд 24
- 25. ВЫВОДЫ:В результате проделанной работы выяснилось, что
- 26. Слайд 26
- 27. УВАЖАЕМЫЕ РАБОТНИКИ РАЙОННОГО ОТДЕЛА ОБРАЗОВАНИЯ ОБУЧАЮЩИЕСЯ МБОУ
- 28. Список использованной литературы Я познаю мир: Детская
Тверской Путевой дворецВладельцы усадьбы: 1766 – нач. XIX в. – императорская резиденция, нач. XIX в. – губернаторская резиденция, 1838—1839 гг. - военное ведомство, 1898 – 1917 гг. – резиденция тверских губернаторов. Архитектор усадьбы: Петр Никитин, Матвей Казаков,
Слайд 1МБОУ «Краснохолмская сош № 2 им. С. Забавина Исследовательская работа «Математика в архитектуре
Тверского Императорского Путевого дворца»
Слайд 2Тверской Путевой дворец
Владельцы усадьбы: 1766 – нач. XIX в. – императорская
резиденция, нач. XIX в. – губернаторская резиденция, 1838—1839 гг. - военное ведомство, 1898 – 1917 гг. – резиденция тверских губернаторов.
Архитектор усадьбы: Петр Никитин, Матвей Казаков, Карл Росси, А.И. Резанов.
Слайд 3МАТЕМАТИКА В АРХИТЕКТУРЕ
Когда я услышала словосочетание «математика в архитектуре», я задалась
вопросом – а существует ли действительно математика в архитектуре? Несомненно, достаточно взглянуть на здания, и мы увидим геометрические фигуры: параллелепипед, треугольные фронтоны, полукруглые окна… И это всего лишь малая часть фигур, которые радуют наши глаза своей красотой. Возникает вопрос- «что же такое архитектура»? Архитектура- это система зданий и сооружений, формирующие пространственную среду для жизни и деятельности людей.
Слайд 4
Актуальность
Математика – один из путеводителей в архитектуре. Математические действие необходимы для реализации проектов в строительстве.
привитие интереса к математике; которое способствует формированию представления о прикладных возможностях математики, её связи с архитектурой.
Цель: выявить, насколько широко математика присутствует в
архитектурных сооружениях
Слайд 5 Задачи:
-расширить сферу
математических знаний
-убедиться в практической необходимости владения способами выполнения математических действий
- развивать стремление к познанию истории математики; истории архитектуры;
- расширить общекультурный кругозор посредством знакомства с лучшими образцами произведений архитектуры;
- раскрыть возможности применения полученных знаний в своей будущей профессии художника, архитектора, инженера, строителя.
-исследовать архитектурное сооружение Тверской Путевой Дворец, при проектировании которого использовалась симметрия
-убедиться в практической необходимости владения способами выполнения математических действий
- развивать стремление к познанию истории математики; истории архитектуры;
- расширить общекультурный кругозор посредством знакомства с лучшими образцами произведений архитектуры;
- раскрыть возможности применения полученных знаний в своей будущей профессии художника, архитектора, инженера, строителя.
-исследовать архитектурное сооружение Тверской Путевой Дворец, при проектировании которого использовалась симметрия
Слайд 6Гипотеза
Многим трудно поверить, что искусство может свободно уживаться с точной наукой.
Однако мастера былых эпох постоянно стремились проверить математикой гармонию, ни один шаг в их работе не обходился без опоры на науку.
Итак, если будут найдены единые критерии прекрасного, объединяющие различные архитектурные объекты, значит существует связь между математическими законами и свойствами и общими формулами красоты
математика (в данном случае симметрия) широко использована при проектировании архитектурного сооружения Тверского Путевого Дворца и оформлении фасадов зданий.
Итак, если будут найдены единые критерии прекрасного, объединяющие различные архитектурные объекты, значит существует связь между математическими законами и свойствами и общими формулами красоты
математика (в данном случае симметрия) широко использована при проектировании архитектурного сооружения Тверского Путевого Дворца и оформлении фасадов зданий.
Слайд 7История Путевого Дворца
Дворец с двумя павильонами был построен в 1764-1966 г. в стиле классицизм с
элементами барокко по проекту П. Р. Никитина.
Дворец предназначался для отдыха членов императорской семьи по пути из Петербурга в Москву, откуда и получил своё название. 12 февраля 1767 года в Тверской дворец впервые прибыла императрица Екатерина.
Дворец был перестроен К. И. Росси в начале XIX века. В это время здесь жила сестра Александра I, Екатерина Павловна, бывшая замужем за тверским губернатором. Она превратила дворец в один из центров светской жизни страны и модный литературный салон, где собиралось высшее общество Твери и куда приезжали многие выдающиеся люди из Москвы и Петербурга. Н. М. Карамзин читал здесь императору Александру отрывки из своей «Истории».
В 1864 году дворец был незаметно и тонко дополнен А.И. Резановым, предпринявшим очередную перестройку, на этот раз в «старом вкусе», так что отличить со стороны его дополнения от исторического здания Никитина очень сложно.
В здании путевого дворца работали советы рабочих и крестьянских депутатов, а также губернский исполнительный комитет. 28 октября (10 ноября) революционер А. П. Вагжанов объявил о победе советской власти. Осенью 1941 года здание частично разрушено фашистами, в 1942—1948 гг. восстановлено.
В настоящее время в Путевом дворце расположена областная картинная галерея. С конца 1990-х годов Путевой дворец находится на реконструкции. С августа 2012 закрыт окончательно на реставрацию
В 2017 году дворец открылся в тестовом режиме — для организованных экскурсионных групп, ожидается открытие всего ансамбля для индивидуальных посетителей.
Дворец предназначался для отдыха членов императорской семьи по пути из Петербурга в Москву, откуда и получил своё название. 12 февраля 1767 года в Тверской дворец впервые прибыла императрица Екатерина.
Дворец был перестроен К. И. Росси в начале XIX века. В это время здесь жила сестра Александра I, Екатерина Павловна, бывшая замужем за тверским губернатором. Она превратила дворец в один из центров светской жизни страны и модный литературный салон, где собиралось высшее общество Твери и куда приезжали многие выдающиеся люди из Москвы и Петербурга. Н. М. Карамзин читал здесь императору Александру отрывки из своей «Истории».
В 1864 году дворец был незаметно и тонко дополнен А.И. Резановым, предпринявшим очередную перестройку, на этот раз в «старом вкусе», так что отличить со стороны его дополнения от исторического здания Никитина очень сложно.
В здании путевого дворца работали советы рабочих и крестьянских депутатов, а также губернский исполнительный комитет. 28 октября (10 ноября) революционер А. П. Вагжанов объявил о победе советской власти. Осенью 1941 года здание частично разрушено фашистами, в 1942—1948 гг. восстановлено.
В настоящее время в Путевом дворце расположена областная картинная галерея. С конца 1990-х годов Путевой дворец находится на реконструкции. С августа 2012 закрыт окончательно на реставрацию
В 2017 году дворец открылся в тестовом режиме — для организованных экскурсионных групп, ожидается открытие всего ансамбля для индивидуальных посетителей.
Слайд 13Архитектура
Архитектура – древнейшая сфера человеческой деятельности («искусство строить» – по определению
Альберти) и ее результат. Главный смысл понятия архитектура состоит в том, что это совокупность зданий и сооружений различного назначения, это пространство, созданное человеком и необходимое для его жизни и деятельности. Архитектура зарождается вместе с человечеством, сопровождает его в историческом развитии. В ней отражаются мировоззрение, ценности, знания людей, живших в различные исторические эпохи. В ней сосредоточены особенности культуры представителей разных национальностей. Архитектурные памятники, дошедшие до нас из глубины веков, помогают нам понять цели, взгляды, мысли, традиции и привычки,
Слайд 14Связь математики и архитектуры
Фундаментальные закономерности математики являются формообразующими в архитектуре, что
архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга. Они давали друг другу новые идеи и стимулы, совместно ставили и решали задачи. По сути, каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой.
В построении архитектурных зданий используются математические принципы.
Для создания линейных орнаментов используются следующие преобразования:
а) параллельный перенос; б) зеркальная симметрия с вертикальной осью; в) зеркальная симметрия с горизонтальной осью; г) поворотная (центральная симметрия).
В построении архитектурных зданий используются математические принципы.
Для создания линейных орнаментов используются следующие преобразования:
а) параллельный перенос; б) зеркальная симметрия с вертикальной осью; в) зеркальная симметрия с горизонтальной осью; г) поворотная (центральная симметрия).
Слайд 15Виды симметрии:
В архитектуре часто используются разные виды симметрии.
С греческого «Симметрия»
означает «пропорциональность, соразмерность, одинаковость в расположении частей».
Современные архитекторы из разных стран до сих пор используют в своей работе опыт старых мастеров: проверенные временем золотую пропорцию и симметрию.
Современные архитекторы из разных стран до сих пор используют в своей работе опыт старых мастеров: проверенные временем золотую пропорцию и симметрию.
Слайд 16Как математика помогает планировать архитектурные объекты
При составлении плана здания наиболее часто
решаются геометрические задачи о разбиении многоугольника на части. При решение таких задач применяется понятие масштаб. Масштаб позволяет наблюдать фигуру с разных сторон.
Слайд 17Как математика помогает добиться прочности сооружений
Прочность зданий обеспечивается не только материалом,
но и конструкцией, которая нужна для основы при его проектировании и строительстве.
Прочность постройки взаимосвязана с его геометрической формой, которая является для нее базовой. Самым прочным архитектурным сооружением является египетские пирамиды.
Прочность постройки взаимосвязана с его геометрической формой, которая является для нее базовой. Самым прочным архитектурным сооружением является египетские пирамиды.
Слайд 18Переносная симметрия обычно используется при построении бордюров. В произведениях архитектурного искусства
ее можно увидеть в орнаментах или решетках, которые используются для их украшения. Переносная симметрия используется и в интерьерах зданий.
Слайд 19Крестообразные купола в основании павильоны на концах крыльев дворца имеют в
завершении круглый объем со сферическим куполом, увенчанный цилиндрическим барабаном, также с купольной кровлей.
Слайд 20
Ампирные фасады дополнились наличниками, рустовками, тягами, филенками и гирляндами.
Подобный набор элементов декора характерен для так называемого стиля Людовика XVI, популярного на тот момент в столичной архитектуре. Также были установлены дошедшие до нашего времени скульптурные фигуры аттика и два больших балкона перед фасадами центрального входа.
Подобный набор элементов декора характерен для так называемого стиля
Людовика XVI, популярного на тот момент в столичной архитектуре. Также были установлены дошедшие до нашего времени скульптурные фигуры аттика и два больших балкона перед фасадами центрального входа.
Подобный набор элементов декора характерен для так называемого стиля
Людовика XVI, популярного на тот момент в столичной архитектуре. Также были установлены дошедшие до нашего времени скульптурные фигуры аттика и два больших балкона перед фасадами центрального входа.
Слайд 21После того, как все детали, элементы здания поострены, на план наносят
все необходимые расчет, надписи и размеры.
Слайд 22 Итак, математические расчеты, измерения, построения – это самые важные и
незаменимые методы для архитектора
Слайд 25ВЫВОДЫ:
В результате проделанной работы выяснилось, что математика и архитектура перекликаются между
собой. Для разных архитектурных стилей характерен определенный набор различных геометрических фигур и их отдельных элементов. С развитием строительных технологий возможности применения геометрических форм расширяются.
Мы провели исследование среди обучающихся школы и узнали следующие моменты:
50% ребят считают, что математические знания нужны в архитектуре;
20% считают, что математика помогает добиться прочность сооружений
Мы провели исследование среди обучающихся школы и узнали следующие моменты:
50% ребят считают, что математические знания нужны в архитектуре;
20% считают, что математика помогает добиться прочность сооружений
Слайд 26 Заключение
Таким образом, тема
проекта актуальна, особенно на нынешнем этапе развития архитектуры. Сложно представить современное градостроительство без математических моделей-прогнозов.
Возникла возможность создавать модели максимально возможно приближенные к реальности, применяя современные и традиционные разделы математики при увеличении скорости просчета вариантов.
Архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга. Они давали друг другу новые идеи и стимулы, совместно ставили и решали задачи. По сути, каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой.
Возникла возможность создавать модели максимально возможно приближенные к реальности, применяя современные и традиционные разделы математики при увеличении скорости просчета вариантов.
Архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга. Они давали друг другу новые идеи и стимулы, совместно ставили и решали задачи. По сути, каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой.
Слайд 27УВАЖАЕМЫЕ РАБОТНИКИ РАЙОННОГО ОТДЕЛА ОБРАЗОВАНИЯ
ОБУЧАЮЩИЕСЯ МБОУ «КРАСНОХОЛМСКАЯ СРЕДНЯЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
№ 2 ИМ. С. ЗАБАВИНА ВЫРАЖАЕТ ИСКРЕННЮЮ БЛАГОДАРНОСТЬ РАЙОННОМУ ОБРАЗОВАТЕЛЬНОМУ ОТДЕЛУ Г, КРАСНЫЙ ХОЛМ В ОРГАНИЗАЦИИ НАШЕЙ ЭКСКУРСИОННОЙ ПОЕЗДКИ В ТВЕРСКОЙ ИМПЕРАТОРСКИЙ ПУТЕВОЙ ДВОРЕЦ .
МЫ ПОЛУЧИЛИ ОГРОМНОЕ УДОВОЛЬСТВИЕ, ПРИОБЩЕНИЕ К ИСТОРИЧЕСКИМ АРХИТЕКТУРНЫМ ПАМЯТНИКАМ КУЛЬТУРЫ И НОВЫЕ НЕИЗГЛАДИМЫЕ ВПЕЧАТЛЕНИЯ!
СПАСИБО ВАМ!
МЫ ПОЛУЧИЛИ ОГРОМНОЕ УДОВОЛЬСТВИЕ, ПРИОБЩЕНИЕ К ИСТОРИЧЕСКИМ АРХИТЕКТУРНЫМ ПАМЯТНИКАМ КУЛЬТУРЫ И НОВЫЕ НЕИЗГЛАДИМЫЕ ВПЕЧАТЛЕНИЯ!
СПАСИБО ВАМ!
Слайд 28Список использованной литературы
Я познаю мир: Детская энциклопедия.Архитектура.1990
Что такое Кто такой. Том1,2.издательство
«Педагогика», 1990.
Л.С.Атанасян Геометрия 7-9, 10-11.Москва «Просвещение» 2005
Большая энциклопедия Кирилла и Мефодия. Электронное издание.
http ://www.elohovo.narod.ru.
http ://www.ru.wikipedia.org.
http ://www.hist-singhts.ru
http ://www.museum.ru
Л.С.Атанасян Геометрия 7-9, 10-11.Москва «Просвещение» 2005
Большая энциклопедия Кирилла и Мефодия. Электронное издание.
http ://www.elohovo.narod.ru.
http ://www.ru.wikipedia.org.
http ://www.hist-singhts.ru
http ://www.museum.ru