- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Графы, решение задач
Содержание
- 1. Презентация по теме Графы, решение задач
- 2. Учеников 11-х классов города Соликамска пригласили в
- 3. Можем ли мы сразу решить эту задачу,
- 4. В чем сходство картинок?Схема метрополитенаГенеалогическое древоКомпьютерные сетиФайловая системаГрафический редактор
- 5. Слайд 5
- 6. Тема урока«Графы. Решение задач с использованием графов»
- 7. Цель урока Разработать алгоритм решения задач с помощью графов
- 8. Граф – это совокупность непустого множества вершин
- 9. 1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.2. Неориентированный
- 10. Слайд 10
- 11. Слайд 11
- 12. Результаты129 - 41 минута183 - 37минут150 - 36минут117- 40 минут
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Транспортная задача Однородный груз сосредоточен у
- 19. Слайд 19
- 20. Слайд 20
- 21. Задача коммивояжера. Требуется посетить все вершины графа
- 22. Многие постановки экономического содержания сводятся к задаче
- 23. Пример Решите задачу коммивояжера для четырех городов
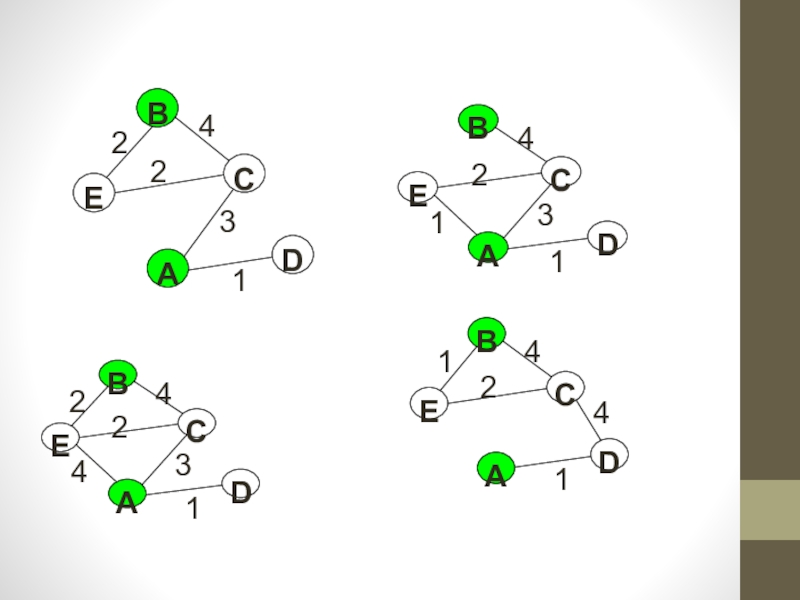
- 24. Построим граф
- 25. Задача
- 26. На рисунке - схема дорог, связывающих города
- 27. Алгоритм решения задачПостроить графЗаписать возможные варианты маршрутовЗаписать
- 28. РефлексияВыбрать любые два предложения и продолжить их• сегодня
- 29. Задача 3 Поиск количества путейНа рисунке изображена
- 30. Решение задачиКратчайший путь: 1 5 9. Его
- 31. Спасибо за работу на уроке!
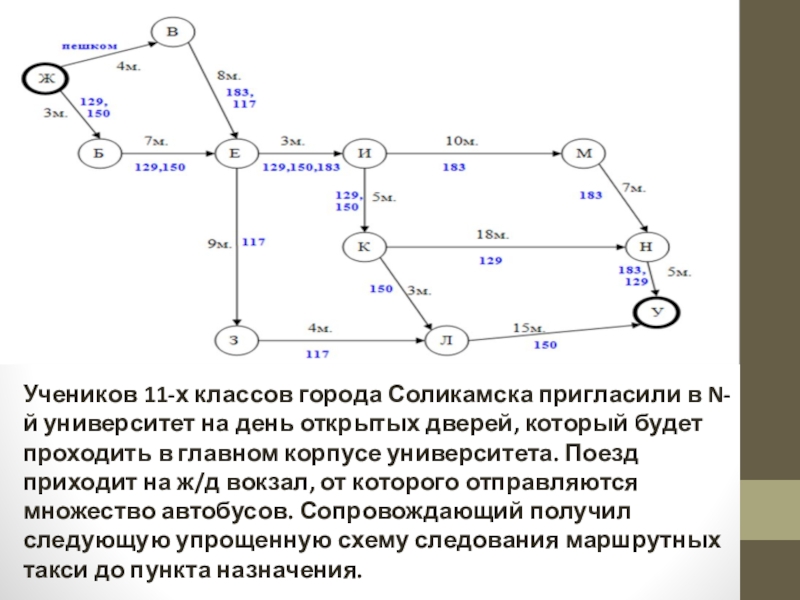
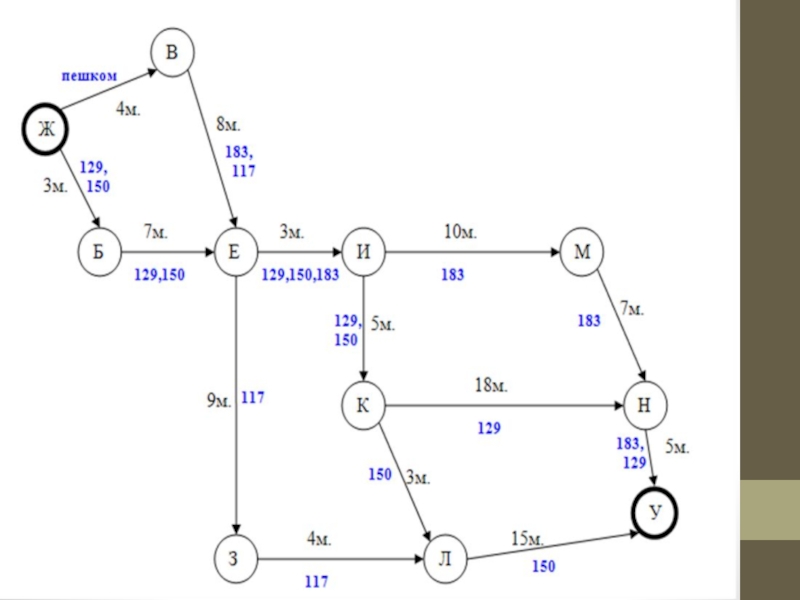
Учеников 11-х классов города Соликамска пригласили в N-й университет на день открытых дверей, который будет проходить в главном корпусе университета. Поезд приходит на ж/д вокзал, от которого отправляются множество автобусов. Сопровождающий получил следующую упрощенную схему следования
Слайд 2Учеников 11-х классов города Соликамска пригласили в N-й университет на день
открытых дверей, который будет проходить в главном корпусе университета. Поезд приходит на ж/д вокзал, от которого отправляются множество автобусов. Сопровождающий получил следующую упрощенную схему следования маршрутных такси до пункта назначения.
Слайд 3Можем ли мы сразу решить эту задачу, только посмотрев на схему?
Что нам мешает решить задачу?
Что нужно сделать чтобы решить задачу?
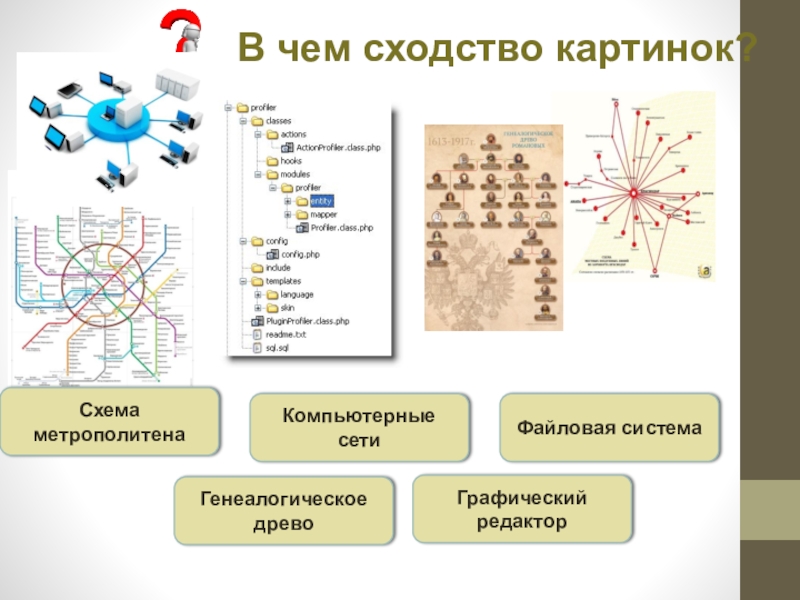
Слайд 4В чем сходство картинок?
Схема метрополитена
Генеалогическое древо
Компьютерные сети
Файловая система
Графический редактор
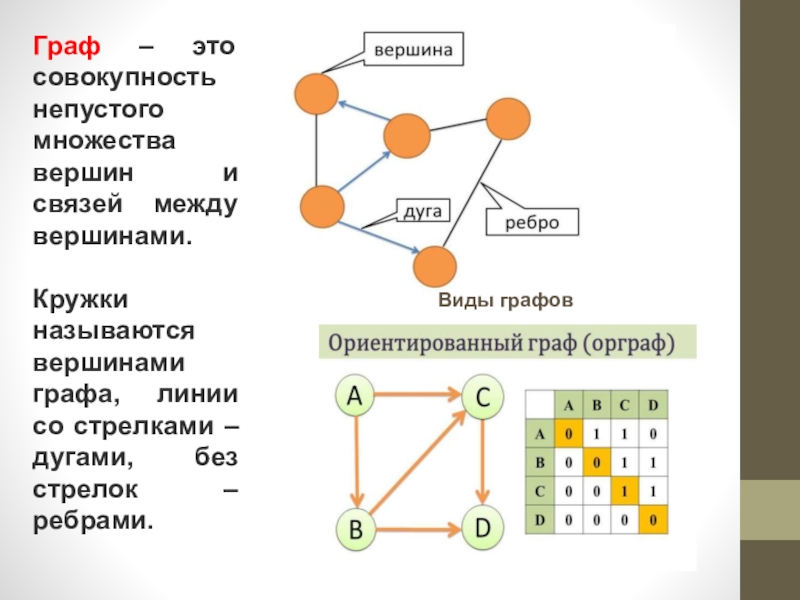
Слайд 8Граф – это совокупность непустого множества вершин и связей между вершинами.
Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.
Виды графов
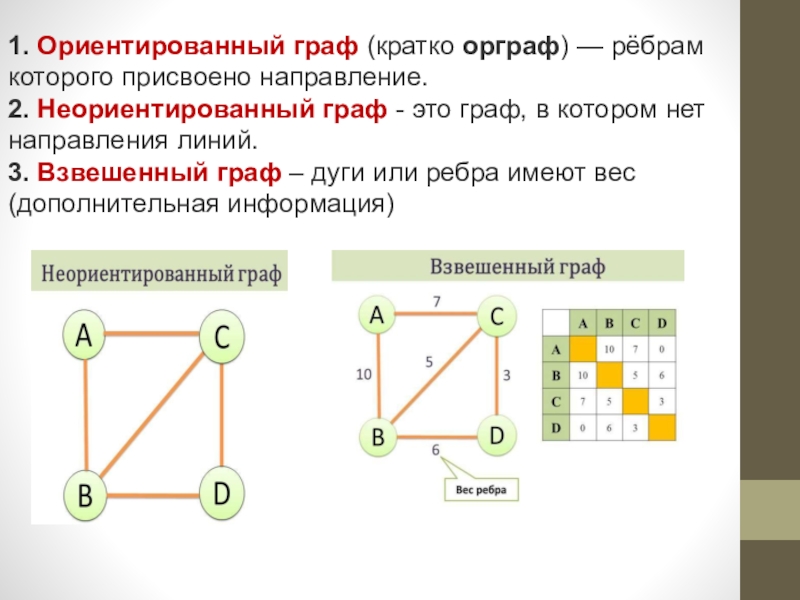
Слайд 91. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.
2. Неориентированный граф - это граф, в котором
нет направления линий.
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация)
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация)
Слайд 18Транспортная задача
Однородный груз сосредоточен у m поставщиков , данный
груз необходимо доставить n потребителям. Известны стоимости перевозок. Требуется составить такой план перевозок, чтобы запасы всех поставщиков были вывезены, запросы всех потребителей удовлетворены и суммарные затраты на перевозку всех грузов были минимальны.
Слайд 21Задача коммивояжера.
Требуется посетить все вершины графа и вернуться в исходную
вершину, минимизировав затраты на проезд (или минимизировав время).
Исходные данные здесь - это граф, дугам которого приписаны положительные числа - затраты на проезд или время, необходимое для продвижения из одной вершины в другую. В общем случае граф является ориентированным, и каждые две вершины соединяют две дуги - туда и обратно.
Действительно, если пункт А расположен на горе, а пункт Б - в низине, то время на проезд из А в Б, очевидно, меньше времени на обратный проезд из Б в А.
Исходные данные здесь - это граф, дугам которого приписаны положительные числа - затраты на проезд или время, необходимое для продвижения из одной вершины в другую. В общем случае граф является ориентированным, и каждые две вершины соединяют две дуги - туда и обратно.
Действительно, если пункт А расположен на горе, а пункт Б - в низине, то время на проезд из А в Б, очевидно, меньше времени на обратный проезд из Б в А.
Слайд 22Многие постановки экономического содержания сводятся к задаче коммивояжера. Например:
составить наиболее выгодный
маршрут обхода наладчика в цехе (контролера, охранника, милиционера), отвечающего за должное функционирование заданного множества объектов (каждый из этих объектов моделируется вершиной графа);
составить наиболее выгодный маршрут доставки деталей рабочим или хлеба с хлебозавода по заданному числу булочных и других торговых точек (парковка у хлебозавода).
составить наиболее выгодный маршрут доставки деталей рабочим или хлеба с хлебозавода по заданному числу булочных и других торговых точек (парковка у хлебозавода).
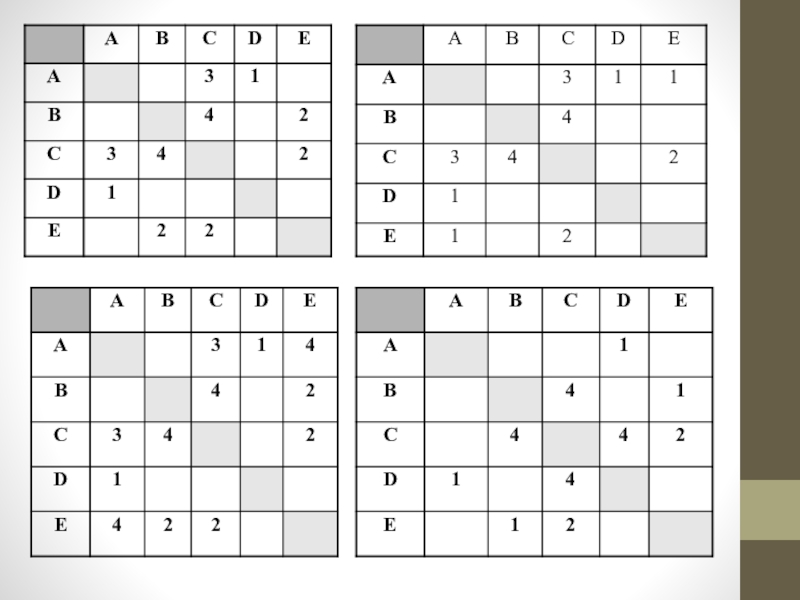
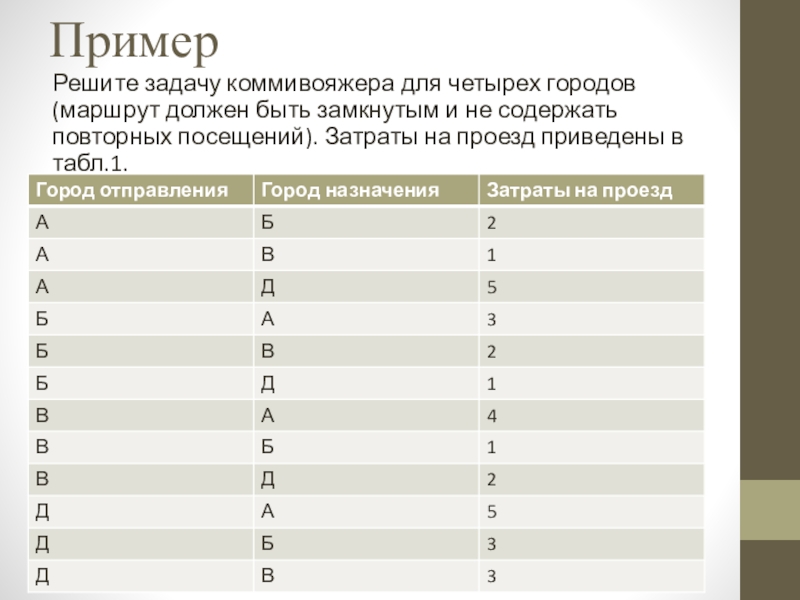
Слайд 23Пример
Решите задачу коммивояжера для четырех городов (маршрут должен быть замкнутым
и не содержать повторных посещений). Затраты на проезд приведены в табл.1.
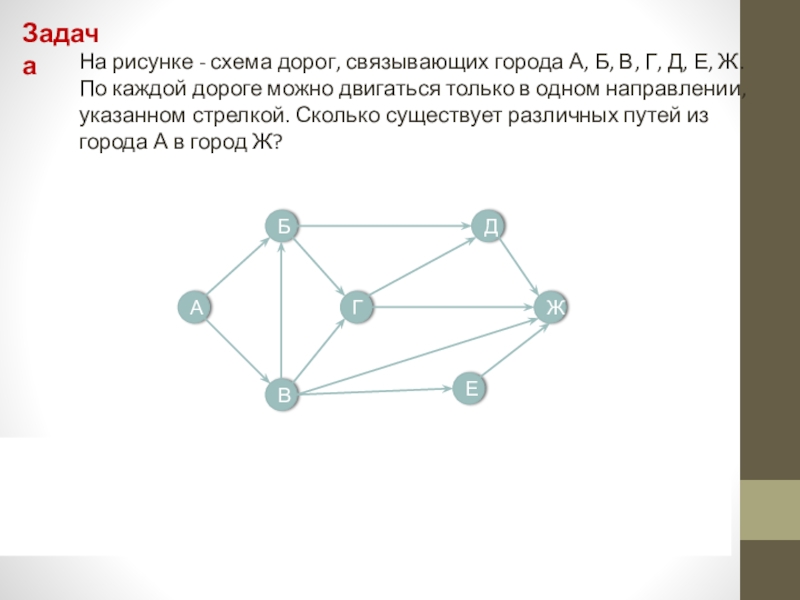
Слайд 26На рисунке - схема дорог, связывающих города А, Б, В, Г,
Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
А
Б
В
Г
Д
Ж
Е
1. А-Б-Д-Ж
2. А-Б-Г-Д-Ж
3. А-Б-Г-Ж
4. А-В-Б-Д-Ж
5. А-В-Б-Г-Д-Ж
6. А-В-Б-Г-Ж
7. А-В-Г-Д-Ж
8. А-В-Г-Ж
9. А-В-Ж
10. А-В-Е-Ж
Ответ: 10 путей
Задача
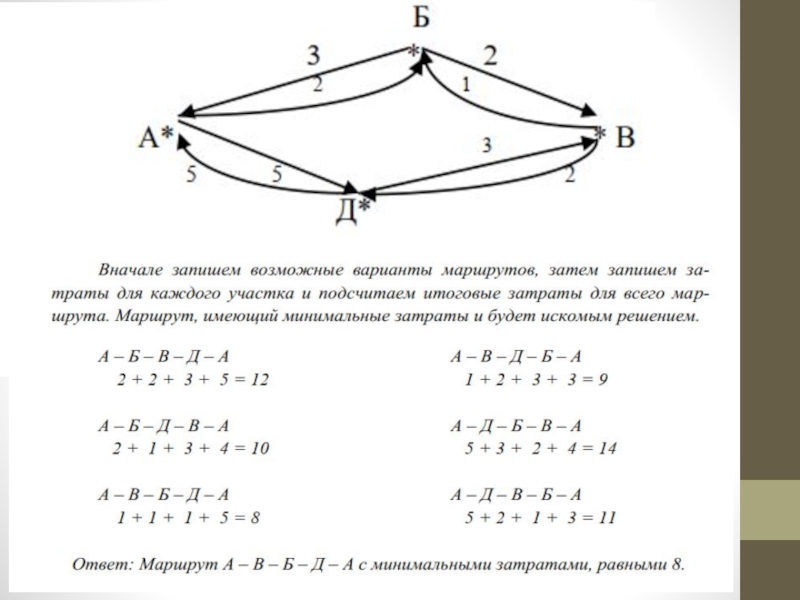
Слайд 27Алгоритм решения задач
Построить граф
Записать возможные варианты маршрутов
Записать затраты для каждого участка
Подсчитать
итоговые затраты для каждого маршрута.
Маршрут, имеющий минимальные затраты и будет искомым решением.
Маршрут, имеющий минимальные затраты и будет искомым решением.
Слайд 28Рефлексия
Выбрать любые два предложения и продолжить их
• сегодня я узнал...
• было трудно…
• я понял,
что…
• я научился…
• я смог…
• было интересно узнать, что…
• меня удивило…
• мне захотелось…
• свою работу на уроке я оцениваю…..
• моя группа работала…
• в группе мне было работать…….
• я научился…
• я смог…
• было интересно узнать, что…
• меня удивило…
• мне захотелось…
• свою работу на уроке я оцениваю…..
• моя группа работала…
• в группе мне было работать…….
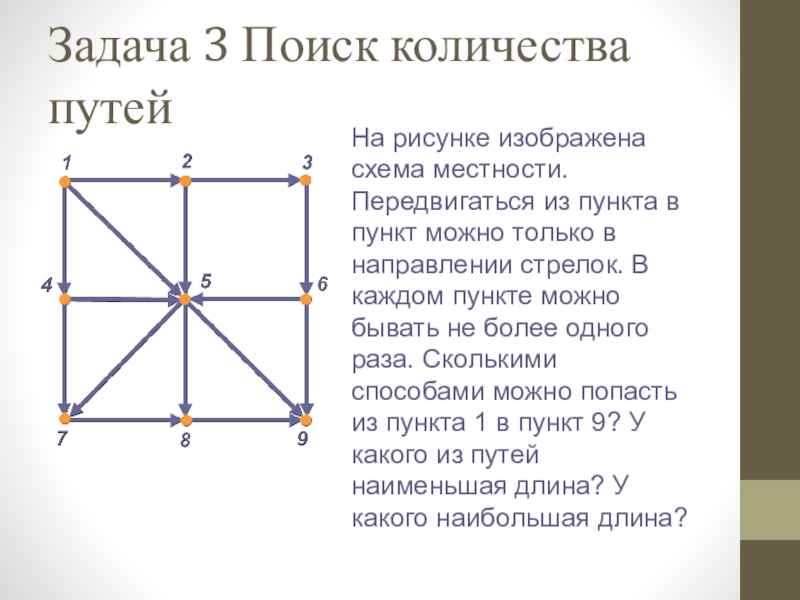
Слайд 29Задача 3 Поиск количества путей
На рисунке изображена схема местности. Передвигаться из
пункта в пункт можно только в направлении стрелок. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из путей наименьшая длина? У какого наибольшая длина?
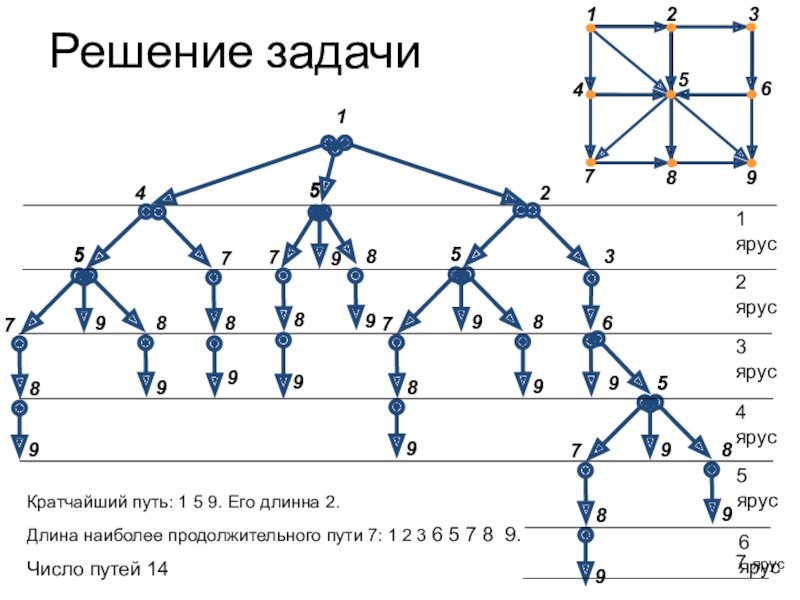
Слайд 30Решение задачи
Кратчайший путь: 1 5 9. Его длинна 2.
Длина наиболее продолжительного
пути 7: 1 2 3 6 5 7 8 9.
Число путей 14
Число путей 14