- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по статистике на тему Средние величины
Содержание
- 1. Презентация по статистике на тему Средние величины
- 2. Средняя величина -это обобщенная количественная характеристика
- 3. Виды средних показателейСредняя арифметическая: 1) Простая;
- 4. Средняя арифметическая простая (невзвешенная) Используется
- 5. Пример №1 В
- 6. Решение Xср =
- 7. Средняя арифметическая взвешенная Расчет
- 8. Пример №2 Определить среднемесячную заработную плату в магазине канцтоваров «Осень»
- 9. Решение Х1 = 7000 + 8000 /
- 10. Средняя гармоническая простая
- 11. Средняя гармоническая взвешенная
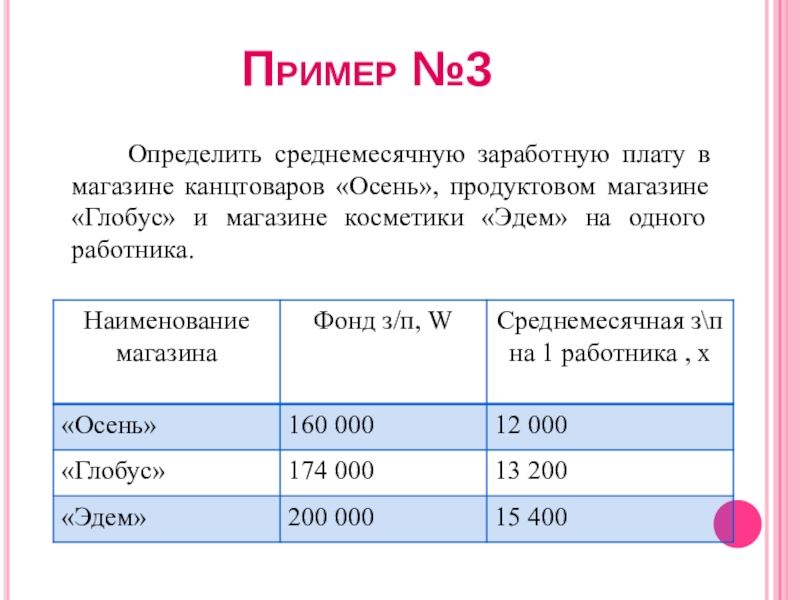
- 12. Пример №3 Определить среднемесячную заработную плату в магазине
- 13. Решение =
- 14. Средняя геометрическая простая
- 15. Пример №4
- 16. Решение
- 17. Средняя геометрическая взвешенная Применяется
Средняя величина -это обобщенная количественная характеристика признака статистической совокупности в конкретных условиях и месте. Средняя величина отражает уровень изучаемого признака приходящегося на единицу совокупности
Слайд 1Средние показатели в статистике
Преподаватель Экономических дисциплин
Т. В. Блинова
Киров, 2019 г.
Слайд 2Средняя величина
-это обобщенная количественная характеристика признака статистической совокупности в
конкретных условиях и месте.
Средняя величина отражает уровень изучаемого признака приходящегося на единицу совокупности
Средняя величина отражает уровень изучаемого признака приходящегося на единицу совокупности
Слайд 3Виды средних показателей
Средняя арифметическая: 1) Простая;
2) Взвешенная.
Средняя гармоническая: 1) Простая;
2) Взвешенная
Средняя геометрическая: 1) Простая;
2) Взвешенная
Средняя гармоническая: 1) Простая;
2) Взвешенная
Средняя геометрическая: 1) Простая;
2) Взвешенная
Слайд 4Средняя арифметическая простая (невзвешенная)
Используется при расчете не сгруппированных
данных
Формула расчета
где xi - величины изучаемого признака у единиц совокупности;
n – количество единиц совокупности.
Формула расчета
где xi - величины изучаемого признака у единиц совокупности;
n – количество единиц совокупности.
Слайд 5Пример №1
В состав работников магазина
канцтоваров «Осень» входит 8 человек имеющие каждый свой стаж работы:
1 человек – 2 года работы;
2 человек – 3 года;
3 человек – 5 лет;
4 человек – 6 лет;
5 человек – 7 лет;
6 человек – 8 лет;
7 человек – 10 лет;
8 человек – 13 лет.
Определить средний стаж работы работников магазина канцтоваров
1 человек – 2 года работы;
2 человек – 3 года;
3 человек – 5 лет;
4 человек – 6 лет;
5 человек – 7 лет;
6 человек – 8 лет;
7 человек – 10 лет;
8 человек – 13 лет.
Определить средний стаж работы работников магазина канцтоваров
Слайд 6Решение
Xср =
= 6,75 = 7 лет
Ответ: Средний стаж работы одного работника в магазине канцтоваров «Осень» составляет 7 лет.
Ответ: Средний стаж работы одного работника в магазине канцтоваров «Осень» составляет 7 лет.
Слайд 7Средняя арифметическая взвешенная
Расчет осуществляется по сгруппированным данным
Если значение признаков даны в виде интервалов, то за Xi принимаются середины интервалов
Формула расчета
где fi - частота повторения
xi =
Формула расчета
где fi - частота повторения
xi =
Слайд 9Решение
Х1 = 7000 + 8000 / 2 = 7500
Х2 =
8000 + 10000 / 2 = 9000
Х3 = 10000 + 12000 / 2 = 11000
Х4 = 12000 + 15000 / 2 = 13500
Х ср =
= 88 000 / 8 = 11 000руб.
Ответ: среднемесячная заработная плата в магазине канцтоваров «Осень» составляет 11 000руб.
Х3 = 10000 + 12000 / 2 = 11000
Х4 = 12000 + 15000 / 2 = 13500
Х ср =
= 88 000 / 8 = 11 000руб.
Ответ: среднемесячная заработная плата в магазине канцтоваров «Осень» составляет 11 000руб.
Слайд 10Средняя гармоническая простая
Показатель, обратный средней арифметической
простой, исчисляемый из обратных значений признака
Условия расчета: величины Wi в группах равны
Формула расчета: =
где m – количество групп
Условия расчета: величины Wi в группах равны
Формула расчета: =
где m – количество групп
Слайд 11Средняя гармоническая взвешенная
-это преобразованная форма среднего
арифметического определяемая если в условии задачи не дана fi
Условия расчета: даны сгруппированные данные и величины Wi в группах различна
Формулы расчета: = - средняя
Wi = xi * fi - сгруппированная
Условия расчета: даны сгруппированные данные и величины Wi в группах различна
Формулы расчета: = - средняя
Wi = xi * fi - сгруппированная
Слайд 12Пример №3
Определить среднемесячную заработную плату в магазине канцтоваров «Осень», продуктовом магазине
«Глобус» и магазине косметики «Эдем» на одного работника.
Слайд 13Решение
=
=
= = 9479руб.85коп.
Ответ: Средняя заработная плата составляет 9 479 рублей 85 копеек
= = 9479руб.85коп.
Ответ: Средняя заработная плата составляет 9 479 рублей 85 копеек
Слайд 14Средняя геометрическая простая
Определяется по относительным показателям
выраженных в коэффициентах или в процентах
Формула расчета ср. геометрической простой:
=
Где n – количество xi
Формула расчета ср. геометрической простой:
=
Где n – количество xi
Слайд 15Пример №4
Необходимо определить средний темп
роста продаж в магазине канцтоваров «Осень» за 2 месяца 2014 года, данные условные.
Слайд 17Средняя геометрическая взвешенная
Применяется для характеристики средних темпов роста
в рядах динамики с неравноотстоящими уровнями
Формула расчета:
=
Формула расчета:
=