Криницина Т.М.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад исследовательской работы со студентами Топология линий. Использование свойств графов при маршрутизации.
Содержание
- 1. Презентация исследовательской работы со студентами Топология линий. Использование свойств графов при маршрутизации.
- 2. Издавна среди жителей Кёнигсберга была распространена такая загадка: как
- 3. Топология линий по другому зовется теория графов.
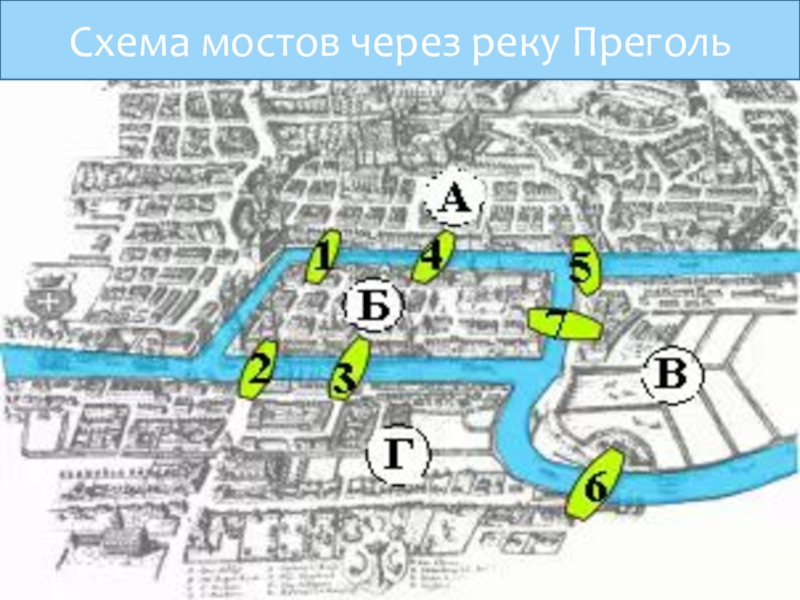
- 4. Схема мостов через реку Преголь
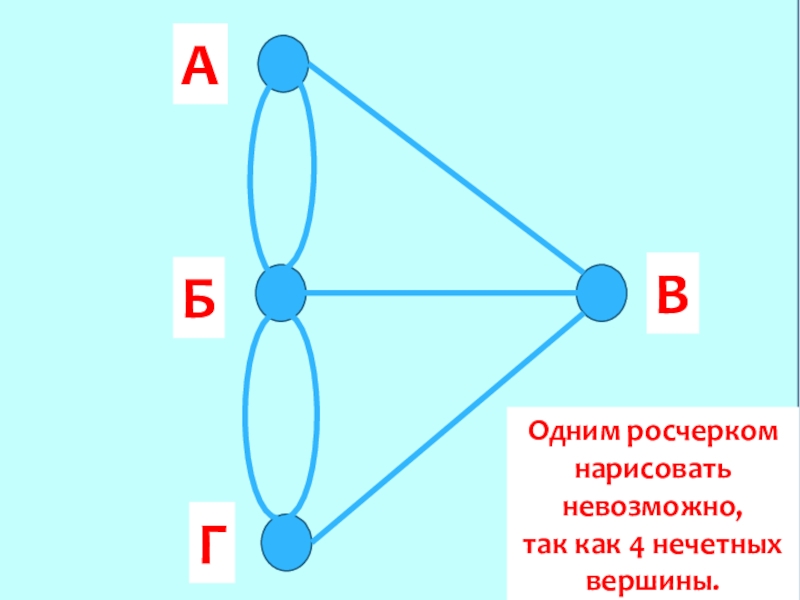
- 5. АГБВОдним росчерком нарисовать невозможно, так как 4 нечетных вершины.
- 6. В ходе рассуждений Эйлер пришёл к следующим
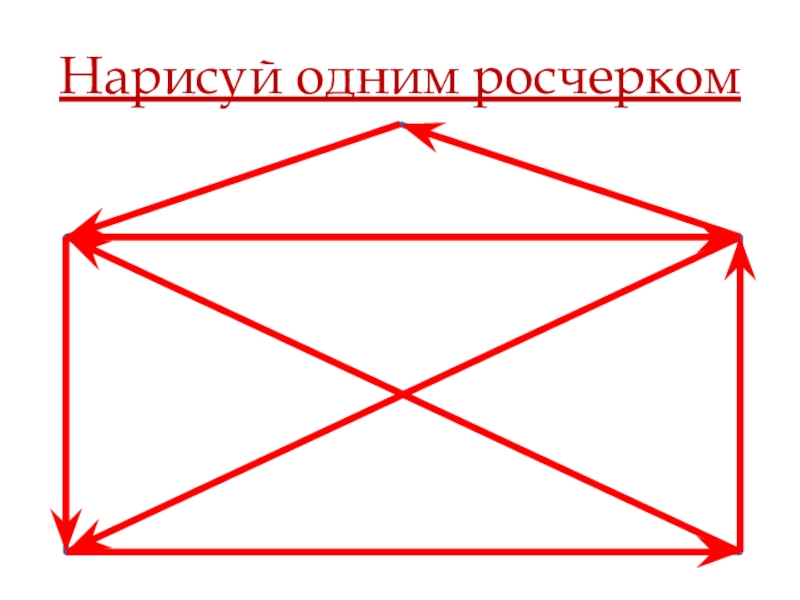
- 7. Нарисуй одним росчерком
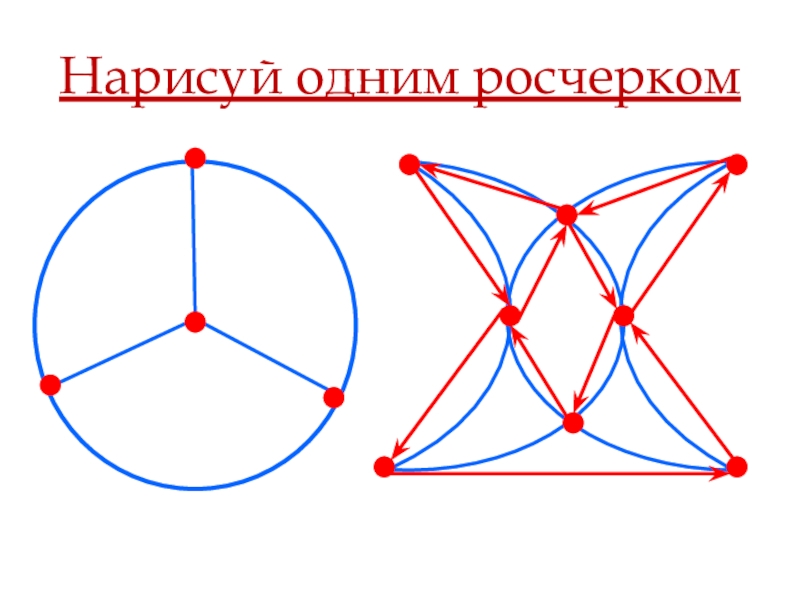
- 8. Нарисуй одним росчерком
- 9. Созданная Эйлером теория графов нашла очень широкое
- 10. Как проехать по мостам г.Красноярска, не проезжая
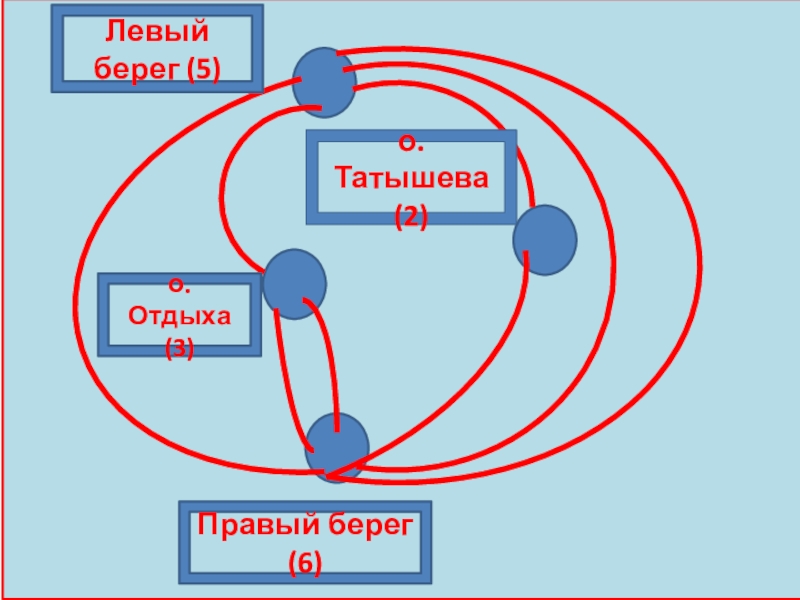
- 11. Левый берег (5)о. Отдыха(3)Правый берег(6)о. Татышева(2)
- 12. Правый берег Левый берег о. Татышевао.
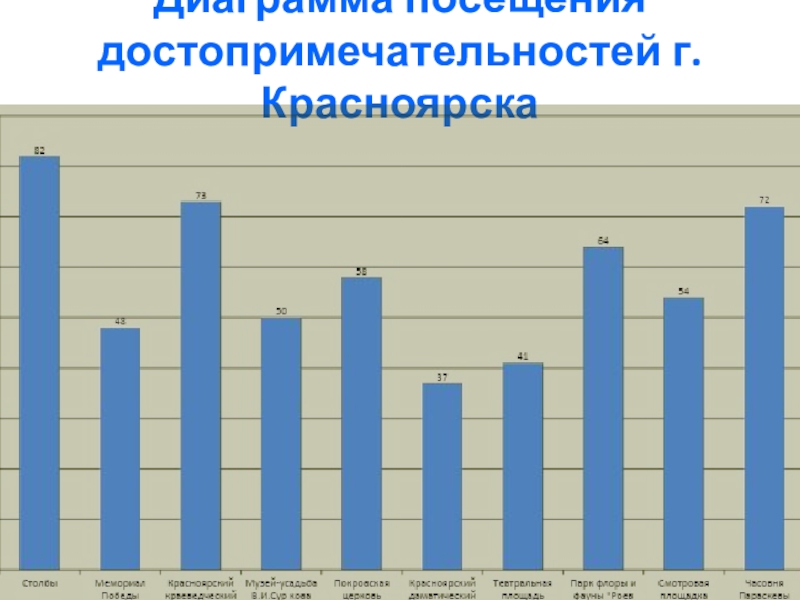
- 13. Диаграмма посещения достопримечательностей г.Красноярска
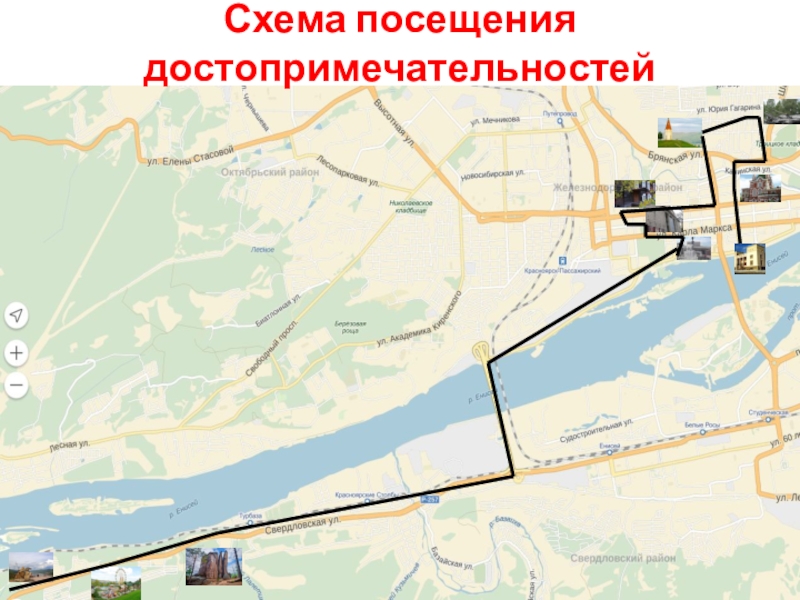
- 14. Схема посещения достопримечательностей
- 15. ВЫВОД : Согласно теории Эйлера : «Граф
- 16. Список использованных источников Березина Л. Ю. Графы
- 17. Спасибо за внимание!!!
Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие жители этого города пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем,
Слайд 1Топология линий.
Использование свойств графов при маршрутизации.
Разработала преподаватель Красноярского политехнического техникума
Слайд 2Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя),
не проходя ни по одному из них дважды. Многие жители этого города пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя».
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя».
Историческая справка
Слайд 3Топология линий по другому зовется теория графов. Граф – это множество
точек, называемых вершинами, некоторые из которых соединены между собой с помощью ребер.
Таким образом, топология зародилась, когда Леонард Эйлер, один из талантливейших математиков в истории, разгадал загадку мостов Кенигсберга. Для этого он использовал граф с четырьмя вершинами и семью ребрами.
Таким образом, топология зародилась, когда Леонард Эйлер, один из талантливейших математиков в истории, разгадал загадку мостов Кенигсберга. Для этого он использовал граф с четырьмя вершинами и семью ребрами.
Историческая справка
Слайд 6В ходе рассуждений Эйлер пришёл к следующим выводам и определил свойства
графа:
1) Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
2) Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
3) Граф с двумя нечётными вершинами возможно начертить одним росчерком (начинаем в одной из них и заканчиваем в другой).
Слайд 9Созданная Эйлером теория графов нашла очень широкое применение в транспортных
и коммуникационных системах (например, для изучения самих систем, составления оптимальных маршрутов доставки грузов или маршрутизации данных в Интернете).
Слайд 10Как проехать по мостам г.Красноярска, не проезжая ни по оному дважды?
С поставленным вопросом легко справиться , если следовать теории Эйлера.
Схема приведена на следующем сайде.
Схема приведена на следующем сайде.
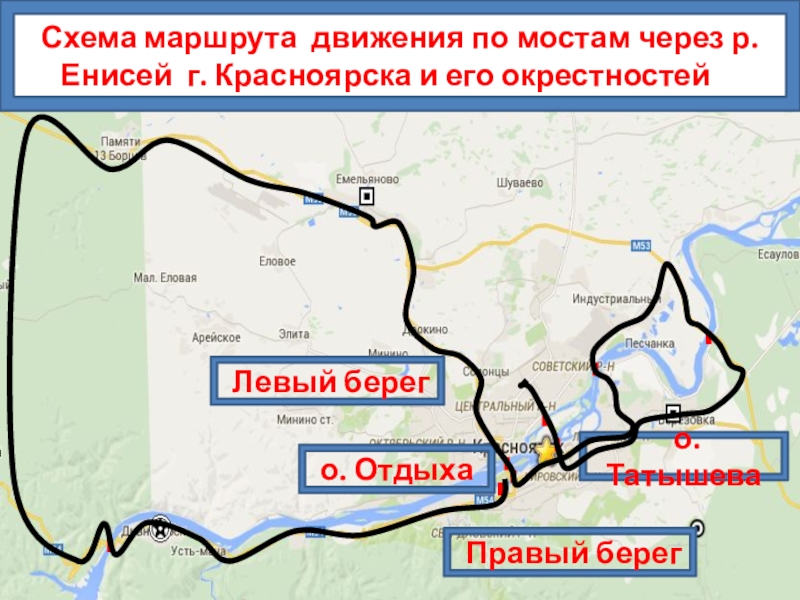
Слайд 12 Правый берег
Левый берег
о. Татышева
о. Отдыха
Схема маршрута движения по
мостам через р. Енисей г. Красноярска и его окрестностей
Слайд 15ВЫВОД :
Согласно теории Эйлера : «Граф с двумя нечётными вершинами
возможно начертить одним росчерком (начинаем в одной из них и заканчиваем в другой)». Под повторный проезд попадают заповедник «Красноярские столбы» и парк флоры и фауны «Роев ручей», что не соответствует нашей гипотезе.
Слайд 16Список использованных источников
Березина Л. Ю. Графы и их применение: пособие для
учителей. - М.: Просвещение, 1979. - 143 с.
Зыков А.А. Основы теории графов. - М.:Наука, 1987, 384 с.
Мельников О.И. Теория графов в занимательных задачах. Изд.3, испр. и доп. 2009. 232 с.
Мельников О.И. Занимательные задачи по теории графов. - Минск: ТетраСистемс, 2001. - 144 с.
Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. (Библиотечка «Квант», Вып. 21).
Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. (Библиотека студента-математика. Вып. 3)
Зыков А.А. Основы теории графов. - М.:Наука, 1987, 384 с.
Мельников О.И. Теория графов в занимательных задачах. Изд.3, испр. и доп. 2009. 232 с.
Мельников О.И. Занимательные задачи по теории графов. - Минск: ТетраСистемс, 2001. - 144 с.
Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. (Библиотечка «Квант», Вып. 21).
Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. (Библиотека студента-математика. Вып. 3)